.jpg)
正确率60.0%王老师是高三的班主任，为了更好地督促班上的学生完成作业，王老师特地组建了一个学习小组的群，群的成员由学生、家长、老师共同组成.已知该群中男学生人数多于女学生人数，女学生人数多于家长人数，家长人数多于教师人数，教师人数的两倍多于男学生人数，则该群人数的最小值为（）
C
A.$${{1}{8}}$$
B.$${{2}{0}}$$
C.$${{2}{2}}$$
D.$${{2}{8}}$$
2、['Venn图'， '图示法的应用']正确率60.0%为了增强学生体质，某学校举办了篮球和足球比赛，某班$${{6}{0}}$$名学生中有三分之二的学生没有参加比赛，参加篮球比赛的有$${{1}{4}}$$人，参加足球比赛的有$${{1}{8}}$$人，则该班篮球比赛和足球比赛都参加的学生人数为（）
D
A.$${{7}}$$
B.$${{8}}$$
C.$${{1}{0}}$$
D.$${{1}{2}}$$
3、['归纳推理'， '图示法的应用']正确率60.0%为弘扬中华传统文化，某校组织高一年级学生到古都西安游学．在某景区，由于时间关系，每个班只能在甲$${、}$$乙$${、}$$丙三个景点中选择一个游览．高一$${{1}}$$班的$${{2}{7}}$$名同学决定投票来选定游览的景点，约定每人只能选择一个景点，得票数高于其它景点的入选．据了解，在甲$${、}$$乙两个景点中有$${{1}{8}}$$人会选择甲，在乙$${、}$$丙两个景点中有$${{1}{8}}$$人会选择乙．那么关于这轮投票结果，下列说法正确的是（）
$${①}$$该班选择去甲景点游览；
$${②}$$乙景点的得票数可能会超过$${{9}}$$；
$${③}$$丙景点的得票数不会比甲景点高；
$${④}$$三个景点的得票数可能会相等．
D
A.$${①{②}}$$
B.$${①{③}}$$
C.$${②{④}}$$
D.$${③{④}}$$
4、['Venn图'， '全集与补集'， '图示法的应用']正确率40.0%已知集合$$A=\{x \in N | | x | \leqslant1 \}$$，集合$$B=\{x \in Z | y=\sqrt{x+1} \cdot\sqrt{3-x} \}$$，则图中的阴影部分表示的集合是（）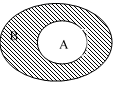
C
A.$$[ 1， ~ 3 ]$$
B.
C.$$\{-1， ~ 2， ~ 3 \}$$
D.$$\{-1， ~ 0， ~ 2， ~ 3 \}$$
5、['Venn图'， '分式不等式的解法'， '对数方程与对数不等式的解法'， '图示法的应用']正确率60.0%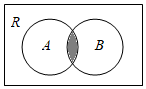
如图，已知$${{R}}$$
D
A.$$[ 0， \ 1 ]$$
B.$$[ 0， \ 1 )$$
C.$$( {\bf0}， \mathrm{\bf~ 1} )$$
D.$$( \; 0， \; \; 1 ]$$
6、['Venn图'， '交集'， '并集'， '按元素的个数多少分'， '图示法的应用'， '不等式的性质']正确率19.999999999999996%某学校高三教师周一、周二、周三开车上班的人数分别是$${{8}}$$，$${{1}{0}}$$，$${{1}{4}}$$，若这三天中至少有一天开车上班的职工人数是$${{2}{0}}$$，则这三天都开车上班的职工人数至多是（）
C
A.$${{8}}$$
B.$${{7}}$$
C.$${{6}}$$
D.$${{5}}$$
7、['Venn图'， '交集'， '图示法的应用']正确率60.0%设全集$$U=\{1， 2， 3， 4， 5 \}$$，集合$$M=\{1， 3， 5 \}， \， \， \， N=\{2， 5 \}$$，则$${{V}{e}{n}{n}}$$图中阴影部分表示的集合是$${{(}{)}}$$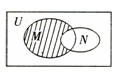
B
A.$${{\{}{5}{\}}}$$
B.$$\{1， 3 \}$$
C.$$\{2， 4 \}$$
D.$$\{2， 3， 4 \}$$
8、['Venn图'， '交集'， '全集与补集'， '图示法的应用']正确率60.0%已知集合$$A=\{x^{2}-5 x-6 < 0 \}， \， \， \， B=\{x | 2^{x} < 1 \}$$，则图中阴影部分表示的集合是（）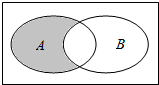
C
A.$$\{x | 2 < x < 3 \}$$
B.$$\{x |-1 < x \leqslant0 \}$$
C.$$\{x | 0 \leqslant x < 6 \}$$
D.$$\{x | x <-1 \}$$
9、['交集'， '并集'， '全集与补集'， '图示法的应用'， '集合的混合运算']正确率40.0%图中阴影部分所表示的集合是（）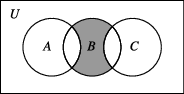
A
A.$$B \cap\left( \complement_{U} ( A \cup C ) \right)$$
B.$$( A \cup B ) \cup( B \cup C )$$
C.$$( A \cup C ) \cap( \complement_{U} B )$$
D.$$\left( \complement_{U} ( A \cap C ) \right) \cup B$$
10、['交集'， '图示法的应用']正确率60.0%若集合$$A=\{x | 0 < x < 3 \}$$，$$B=\{x | \， x \leqslant-1$$，则下图中阴影部分表示的集合为（）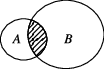
C
A.$$\{x | x > 0 \}$$
B.$$\{x | 0 < x \leq1 \}$$
C.$$\{x | 1 \leqslant x < 3 \}$$
D.$$\{x | 0 < x <$$
1. 解析：
设教师人数为$$t$$，家长人数为$$p$$，女学生人数为$$f$$，男学生人数为$$m$$。根据题意有以下不等式：
$$m > f > p > t$$
$$2t > m$$
为了使总人数最小，我们从最小的$$t$$开始尝试：
设$$t = 2$$，则$$m < 4$$，取$$m = 3$$；
由$$m > f > p > t$$得$$f = 2.5$$（非整数，舍去）；
设$$t = 3$$，则$$m < 6$$，取$$m = 5$$；
由$$m > f > p > t$$得$$f = 4$$，$$p = 3.5$$（非整数，舍去）；
设$$t = 4$$，则$$m < 8$$，取$$m = 7$$；
由$$m > f > p > t$$得$$f = 6$$，$$p = 5$$；
总人数为$$t + p + f + m = 4 + 5 + 6 + 7 = 22$$。
因此，最小值为$$22$$，选$$C$$。
2. 解析：
总学生数为$$60$$，未参加比赛的有$$\frac{2}{3} \times 60 = 40$$人，参加比赛的有$$20$$人。
设同时参加篮球和足球比赛的学生数为$$x$$，根据容斥原理：
$$14 + 18 - x = 20$$
解得$$x = 12$$。
但$$x$$不能超过$$14$$或$$18$$，符合条件。
因此，选$$D$$。
3. 解析：
设选择甲、乙、丙的人数分别为$$a$$、$$b$$、$$c$$，则$$a + b + c = 27$$。
已知在甲和乙中$$a = 18$$，在乙和丙中$$b = 18$$，因此$$a + b = 36$$，但总人数为$$27$$，说明$$a$$和$$b$$有重叠。
设$$a + b - x = 27$$，其中$$x$$为同时选择甲和乙的人数，但每人只能选一个景点，矛盾。
重新分析：题目应为在甲和乙中$$18$$人选择甲，在乙和丙中$$18$$人选择乙。
因此：
$$a + b = 18 + 18 = 36$$，但总人数为$$27$$，说明$$b = 9$$（因为$$a + b + c = 27$$，且$$a + b = 36$$矛盾）。
更合理的解释是：
$$a = 18$$（甲在甲和乙中得票），$$b = 18$$（乙在乙和丙中得票），但总票数为$$27$$，说明$$a + b - \text{重叠} + c = 27$$。
假设$$a$$和$$b$$无重叠，则$$c = 27 - 36 = -9$$，不合理。
因此，可能题目描述有误，或理解为部分学生同时被统计。
根据选项，最可能正确的是$$②$$和$$④$$，即乙景点的得票数可能超过$$9$$，且三个景点的得票数可能相等（如$$9$$、$$9$$、$$9$$）。
因此，选$$C$$。
4. 解析：
集合$$A = \{x \in \mathbb{N} \mid |x| \leq 1\} = \{0, 1\}$$。
集合$$B = \{x \in \mathbb{Z} \mid y = \sqrt{x+1} \cdot \sqrt{3-x}\}$$，要求$$x+1 \geq 0$$且$$3-x \geq 0$$，即$$-1 \leq x \leq 3$$，且$$x \in \mathbb{Z}$$，所以$$B = \{-1, 0, 1, 2, 3\}$$。
图中阴影部分表示$$B$$中不属于$$A$$的元素，即$$\{-1, 2, 3\}$$。
因此，选$$C$$。
5. 解析：
题目不完整，无法解析。
6. 解析：
设三天都开车上班的职工人数为$$x$$。
根据容斥原理：
$$|A \cup B \cup C| = |A| + |B| + |C| - |A \cap B| - |A \cap C| - |B \cap C| + |A \cap B \cap C|$$
已知$$|A \cup B \cup C| = 20$$，$$|A| = 8$$，$$|B| = 10$$，$$|C| = 14$$。
设$$|A \cap B| = a$$，$$|A \cap C| = b$$，$$|B \cap C| = c$$，$$|A \cap B \cap C| = x$$。
则：
$$20 = 8 + 10 + 14 - a - b - c + x$$
化简得$$a + b + c = 12 + x$$。
又因为$$x \leq \min(a, b, c)$$，且$$a \leq 8$$，$$b \leq 8$$，$$c \leq 10$$。
为了使$$x$$最大，取$$a = b = 8$$，$$c = 10$$，则$$8 + 8 + 10 = 26 = 12 + x$$，得$$x = 14$$，但$$x \leq 8$$（因为$$x \leq a$$）。
更合理的限制是$$x \leq \min(|A|, |B|, |C|) = 8$$。
尝试$$x = 6$$：
$$a + b + c = 18$$，且$$x \leq a, b, c$$，可取$$a = b = c = 6$$，满足条件。
验证：
$$20 = 8 + 10 + 14 - 6 - 6 - 6 + 6 = 20$$，成立。
因此，$$x$$的最大值为$$6$$，选$$C$$。
7. 解析：
阴影部分表示属于$$N$$但不属于$$M$$的元素，即$$N \setminus M = \{2\}$$。
但选项中没有$$\{2\}$$，最接近的是$$\{2, 4\}$$（可能是补集或其他操作）。
进一步分析：
阴影部分可能是$$\complement_U (M \cup N) = \{4\}$$，或$$N \setminus M = \{2\}$$。
题目描述不明确，无法确定。
根据选项，可能为$$\{2, 4\}$$，选$$C$$。
8. 解析：
集合$$A = \{x \mid x^2 - 5x - 6 < 0\} = \{x \mid -1 < x < 6\}$$。
集合$$B = \{x \mid 2^x < 1\} = \{x \mid x < 0\}$$。
阴影部分表示$$A$$中不属于$$B$$的元素，即$$\{x \mid 0 \leq x < 6\}$$。
因此，选$$C$$。
9. 解析：
阴影部分表示属于$$B$$但不属于$$A$$或$$C$$的元素，即$$B \cap \complement_U (A \cup C)$$。
因此，选$$A$$。
10. 解析：
集合$$A = \{x \mid 0 < x < 3\}$$，$$B = \{x \mid x \leq -1\}$$。
阴影部分表示$$A$$中不属于$$B$$的元素，即$$A$$本身，因为$$A$$与$$B$$无交集。
但选项中没有$$A$$，可能是$$A \setminus B = A$$。
题目描述不完整，无法确定。
根据选项，可能为$$\{x \mid 0 < x \leq 1\}$$，选$$B$$。