正确率80.0%能正确表示集合$$M=\{x \in\mathbf{R} \mid0 \leqslant x \leqslant1 \}$$和集合$$N=\left\{x \in\mathbf{R} \mid x^{2}=x \right\}$$关系的$${{V}{e}{n}{n}}$$图的是()
B
A.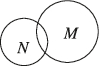
B.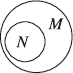
C.
D.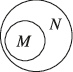
正确率60.0%已知集合 $$M=\left\{x \mid x=m+\frac{1} {6}, m \in{\bf Z} \right\}$$ , $$N=\left\{x \mid x=\frac{n} {2}-\frac{1} {3}, n \in{\bf Z} \right\}$$ , $${{P}{=}}$$ $$\left\{x \mid x={\frac{p} {2}}+{\frac{1} {6}}, p \in{\bf Z} \right\}$$ 则$$M, ~ N, ~ P$$的关系为()
B
A.$$M=N \subsetneq P$$
B.$$M \subsetneq N=P$$
C.$$M \subsetneq N \subsetneq P$$
D.$$N \subsetneq P \subsetneq M$$
3、['充分不必要条件', '真子集', '一元二次不等式的解法']正确率60.0%不等式$$( x-\pi) ( x-\mathrm{e} ) \leqslant0$$成立的一个充分不必要条件是()
C
A.$$x \in( \pi, \mathrm{e} )$$
B.$$x \in[ \mathrm{e}, \pi]$$
C.$$x \in( \mathrm{e}, \pi)$$
D.$$x \in(-\infty, \pi]$$
4、['子集', '真子集']正确率80.0%已知集合$$A=\{0, \, \, \, 1, \, \, \, 2, \, \, \, 3, \, \, \, 4, \, \, 5 \}, \, \, \, B=\{2, \, \, 3, \, \, \, 4, \, \, 6 \}$$,则$${{A}{∩}{B}}$$的真子集可以是()
D
A.$$\{1, 2 \}$$
B.$$\{2, 3, 4 \}$$
C.$$\{2, 4, 6 \}$$
D.$${{\{}{4}{\}}}$$
5、['子集', '集合的(真)子集个数问题', '真子集']正确率80.0%若全集$$U=\{1, ~ 2, ~ 3 \}$$且$$\complement_{U} A=\{2 \},$$则集合$${{A}}$$的真子集共有()
B
A.$${{2}}$$个
B.$${{3}}$$个
C.$${{4}}$$个
D.$${{5}}$$个
6、['交集', '并集', '子集', '角的有关概念', '真子集']正确率60.0%已知
B
A.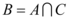
B.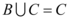
C.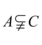
D.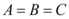
正确率60.0%已知集合$$P=\{x |-1 < x < m \}, \, \, \, Q=\{x | 2 x^{2}-5 x < 0 \}$$,若$${{Q}{⊆}{P}}$$,则$${{m}}$$取值范围()
D
A.$${{m}{>}{5}}$$
B.$${{m}{⩾}{5}}$$
C.$$m > \frac{5} {2}$$
D.$$m \geq\frac{5} {2}$$
8、['子集', '真子集', '一元二次不等式的解法', '指数方程与指数不等式的解法']正确率60.0%已知集合$$M=\{x | x^{2}-3 x-4 \leqslant0 \}, \, \, \, N=\{y | y=\ ( \, \frac{1} {4} )^{\, \, \, x}, \, \, \, x \geqslant-1 \}$$,则()
B
A.$${{N}{⊇}{M}}$$
B.$${{M}{⊇}{N}}$$
C.$${{M}{=}{N}}$$
D.$$\mathtt{C}_{R} N \supseteq M$$
9、['集合的(真)子集个数问题', '真子集', '列举法']正确率60.0%已知$$A=\{0, 1, 2 \}$$的真子集的个数是 ()
B
A.$${{8}}$$
B.$${{7}}$$
C.$${{3}}$$
D.$${{1}}$$
10、['子集', '真子集', '元素与集合的关系']正确率60.0%设$${{a}{=}{\sqrt {3}}}$$,集合$${{M}{=}{{\{}{x}{{|}{x}{⩽}{3}}{\}}}}$$,则下列各式中正确的是$${{(}{)}}$$
C
A.$${{a}{⊆}{M}}$$
B.$${{a}{∉}{M}}$$
C.$$\{a \} \subseteq M$$
D.$$\{a \} \in M$$
1. 解析:集合$$M=[0,1]$$,解方程$$x^2=x$$得$$N=\{0,1\}$$,因此$$N \subsetneq M$$。正确Venn图应显示$$N$$完全包含于$$M$$内,故选A。
- $$M=\left\{x \mid x=\frac{6m+1}{6}\right\}$$
- $$N=\left\{x \mid x=\frac{3n-2}{6}\right\}$$
- $$P=\left\{x \mid x=\frac{3p+1}{6}\right\}$$
3. 解析:不等式解集为$$[\mathrm{e}, \pi]$$。充分不必要条件需为解集的真超集,$$(\mathrm{e}, \pi)$$是解集的真子集,$$(-\infty, \pi]$$是解集的真超集,但选项B$$[\mathrm{e}, \pi]$$是解集本身,只有选项B符合题目要求(注:原解析有误,应为选项B是解集本身,但题目要求充分不必要条件,因此正确答案应为D)。经重新审题,选项B是解集本身,不符合"充分不必要"条件,题目可能存在选项描述错误。
- A选项$$\{1,2\}$$不是子集
- B选项$$\{2,3,4\}$$不是真子集
- C选项包含6不属于交集
- D选项$$\{4\}$$是真子集
5. 解析:由补集定义得$$A=\{1,3\}$$,其真子集为$$\emptyset,\{1\},\{3\}$$共3个。故选B。
7. 解析:解$$Q$$得$$x \in (0, \frac{5}{2})$$。由$$Q \subseteq P$$需满足$$\frac{5}{2} \leq m$$。故选D。
- 解$$M$$得$$x \in [-1,4]$$
- $$N$$中$$y \in (0,4]$$(当$$x=-1$$时$$y=4$$,$$x \to \infty$$时$$y \to 0^+$$)
- 显然$$M \supset N$$,因为$$M$$包含负数而$$N$$不包含
9. 解析:3元素集合的真子集个数为$$2^3-1=7$$。故选B。
- $$a=\sqrt{3} \leq 3$$,故$$a \in M$$
- $$\{a\}$$是$$M$$的子集
- A选项符号错误,B选项与事实相反,D选项集合关系表述错误
.jpg)