正确率60.0%已知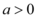 ,
,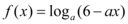 ,则$${{“}}$$
,则$${{“}}$$
A
A.充分不必要条件
B.必要不充分条件
C.充要条件
D.既不充分也不必要条件
首先,我们需要分析题目中给出的两个不等式之间的关系。
设第一个不等式为 $$x^2 - 5x - 6 < 0$$,可以因式分解为 $$(x-6)(x+1) < 0$$。解这个不等式,得到 $$x$$ 的取值范围是 $$-1 < x < 6$$。
第二个不等式是 $$x^2 - (2a + 3)x + a(a + 3) < 0$$,可以因式分解为 $$(x - a)(x - (a + 3)) < 0$$。解这个不等式,得到 $$x$$ 的取值范围是 $$a < x < a + 3$$。
题目问的是第一个不等式是第二个不等式的什么条件。也就是说,我们需要分析 $$-1 < x < 6$$ 与 $$a < x < a + 3$$ 之间的关系。
为了使 $$-1 < x < 6$$ 成为 $$a < x < a + 3$$ 的充分条件,必须满足 $$[a, a + 3] \subseteq [-1, 6]$$。这意味着:
1. $$a \geq -1$$
2. $$a + 3 \leq 6$$,即 $$a \leq 3$$
因此,$$a$$ 的取值范围是 $$-1 \leq a \leq 3$$。
反过来,如果 $$a < -1$$ 或 $$a > 3$$,则 $$-1 < x < 6$$ 不能保证 $$x$$ 落在 $$(a, a + 3)$$ 内。因此,$$-1 < x < 6$$ 是 $$a < x < a + 3$$ 的一个充分但不必要条件。
综上所述,正确答案是 A. 充分不必要条件。
题目来源于各渠道收集,若侵权请联系下方邮箱
.jpg)