.jpg)
正确率60.0%已知命题“非空集合$${{M}}$$中的元素都是集合$${{P}}$$中的元素”是假命题，现有下列命题：
$${{(}{1}{)}{M}}$$中的元素都不是集合$${{P}}$$中的元素；
$${{(}{2}{)}{M}}$$中一定有不属于$${{P}}$$的元素；
$${{(}{3}{)}{M}}$$中一定有属于$${{P}}$$的元素；
$${{(}{4}{)}{M}}$$中的元素不都是集合$${{P}}$$中的元素.
其中真命题是（）
B
A.$$( 1 ) ( 4 )$$
B.$$( 2 ) ( 4 )$$
C.$$( 3 ) ( 4 )$$
D.$$( 1 ) ( 2 )$$
2、['函数奇、偶性的证明'， '或、且、非的综合应用'， '全称量词命题、存在量词命题的真假判断'， '命题的真假性判断']正确率40.0%下列命题中真命题的个数为（）
①$$\forall x \in\mathbf{R}， ~ ~ x^{2}-x+{\frac{1} {4}} \geq0$$；②$$\exists x_{0} > 0， ~ \mathrm{l n} x_{0}+\frac{1} {\mathrm{l n} x_{0}} \leqslant2$$；③若命题$${{p}}$$∨$${{q}}$$是真命题，则$${{¬}{p}}$$是真命题；④$$y=2^{x}-2^{-x}$$是奇函数.
C
A.$${{1}}$$
B.$${{2}}$$
C.$${{3}}$$
D.$${{4}}$$
3、['在R上恒成立问题'， '根据命题的真假求参数范围'， '全称量词命题、存在量词命题的真假判断']正确率40.0%若命题$${{“}{∃}}$$ $${{x}}$$$${_{0}{∈}{R}}$$，使得 $${{x}}$$$${^{2}_{0}{+}}$$ $${{m}{x}}$$$${_{0}{+}{2}}$$ $${{m}}$$$$- 3 < 0^{\prime\prime}$$为假命题，则实数 $${{m}}$$的取值范围是$${{(}{)}}$$
A
A.$$[ 2， 6 ]$$
B.$$[-6，-2 ]$$
C.$$( 2， 6 )$$
D.$$(-6，-2 )$$
4、['全称量词命题、存在量词命题的真假判断'， '直线与平面平行的判定定理'， '平面与平面平行的判定定理']正确率40.0%已知$${{l}}$$表示空间一条直线，$${{α}{、}{β}}$$表示空间两个不重合的平面，有以下三个语句：$$\oplus\l\perp\alpha; \， \odot\l/ / \beta; \， \odot\alpha\perp\beta$$．以其中任意两个作为条件，另外一个作为结论，可以得到三个命题，其中正确命题的个数是（）
B
A.$${{0}}$$
B.$${{1}}$$
C.$${{2}}$$
D.$${{3}}$$
5、['全称量词命题、存在量词命题的真假判断'， '充要条件']正确率60.0%已知命题$$p_{:} \， \， x > 2$$是$$x > l o g_{2} 5$$的必要不充分条件；命题$${{q}}$$：若$$\operatorname{s i n} x=\frac{\sqrt{3}} {3}，$$则$$\operatorname{c o s} 2 x=\operatorname{s i n}^{2} x，$$则下列命题为真命题的是（）
A
A.$${{p}{∧}{q}}$$
B.$$( \sqcap p ) \wedge q$$
C.$$p \wedge\gets q )$$
D.$$( \sp\lnot p ) \wedge( \sp\lnot q )$$
6、['全称量词命题、存在量词命题的真假判断'， '全称量词命题、存在量词命题的否定']正确率60.0%判断下列语句是真命题的为$${{(}{)}}$$．
C
A.若整数$${{a}}$$是素数，则$${{a}}$$是奇数
B.指数函数是增函数吗？
C.若平面上两条直线不相交，则这两条直线平行
D.$${{x}{>}{{1}{5}}}$$
7、['全称量词命题的否定'， '利用导数求曲线的切线方程（斜率）'， '导数的几何意义'， '全称量词命题、存在量词命题的真假判断']正确率40.0%已知函数$$f ( x )=\operatorname{l n} x-a x^{2}-b x$$的图象在点$$( 1， f ( 1 ) )$$处的切线斜率为$${{−}{2}{a}}$$，若命题$${{p}{:}{“}}$$对$$\forall x \in[ 1，+\infty)，$$使得$$f ( x ) \neq0$$成立$${{”}}$$是假命题，则实数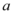
的最小值为（）
B
A.$${{1}}$$
B.$${{−}{1}}$$
C.$${{e}}$$
D.$${{−}{e}}$$
8、['全称量词命题、存在量词命题的真假判断'， '全称量词命题、存在量词命题的否定']正确率60.0%下列关于命题$$\forall x > 0， ~ x^{2} < 2^{x \， n}$$的说法正确的是（）
B
A.真命题，其否定是$$\mathrm{` `} \exists x_{0} \leqslant0， \; \; x_{0}^{2} \geqslant2^{x_{0} \prime\prime}$$
B.假命题，其否定是$$\mathrm{` `} \exists x_{0} > 0， \; \; x_{0}^{2} \geq2^{x_{0} \prime\prime}$$
C.真命题，其否定是$$\mathrm{` `} \exists x_{0} > 0， \; \; x_{0}^{2} \geq2^{x_{0} \prime\prime}$$
D.假命题，其否定是$$\mathrm{` `} \exists x_{0} \leqslant0， \; \; x_{0}^{2} \geqslant2^{x_{0} \prime\prime}$$
9、['全称量词命题的否定'， '全称量词命题、存在量词命题的真假判断']正确率60.0%已知命题$$q \colon\forall x {\in} \mathbf{R}， ~ ~ x^{2} \textsubscript{>} 0$$，则（）
D
A.命题$$\neg q \colon\forall x {\in} \mathbf{R}， ~ ~ x^{2} {\leqslant} 0$$为假命题
B.命题$$\neg q \colon\forall x {\in} \mathbf{R}， ~ ~ x^{2} {\leqslant} 0$$为真命题
C.命题$$\neg q \! : \exists x_{0} \! \in\! \mathbf{R}， \; \; x_{0}^{2} \! \leq\! 0$$为假命题
D.命题$$\neg q \! : \exists x_{0} \! \in\! \mathbf{R}， \; \; x_{0}^{2} \! \leq\! 0$$为真命题
10、['全称量词命题'， '全称量词命题、存在量词命题的真假判断']正确率60.0%下列命题中是全称量词命题，且为假命题的是
（）
D
A.存在一个锐角三角形的内角$${{A}}$$，使得$$\operatorname{s i n} \， A > 1$$
B.任意偶数的$${{3}}$$次方还是偶数
C.$${{∃}{m}{∈}{R}}$$，$$x^{2}+m x+1=0$$无解
D.$${{∀}{x}{∈}{N}}$$，$${{x}^{2}{>}{x}}$$
1. 解析：原命题“非空集合$$M$$中的元素都是集合$$P$$中的元素”是假命题，意味着$$M$$中至少有一个元素不属于$$P$$。
- 命题(1)：“$$M$$中的元素都不是集合$$P$$中的元素”过于绝对，可能为假。
- 命题(2)：“$$M$$中一定有不属于$$P$$的元素”与原命题的否定一致，为真。
- 命题(3)：“$$M$$中一定有属于$$P$$的元素”不一定成立，可能所有元素都不属于$$P$$。
- 命题(4)：“$$M$$中的元素不都是集合$$P$$中的元素”与原命题的否定等价，为真。
因此，真命题是(2)和(4)，选$$B$$。
2. 解析：逐项分析命题的真假。
- ① $$x^2 - x + \frac{1}{4} = (x - \frac{1}{2})^2 \geq 0$$，恒成立，为真。
- ② 若$$x_0 = 1$$，则$$\ln x_0 + \frac{1}{\ln x_0}$$无意义；若$$x_0 = e$$，则值为$$1 + 1 = 2$$，存在满足条件的$$x_0$$，为真。
- ③ 若$$p \lor q$$为真，则至少一个为真，但$$\neg p$$的真假取决于$$p$$的值，不一定为真。
- ④ $$f(-x) = 2^{-x} - 2^x = -(2^x - 2^{-x}) = -f(x)$$，为奇函数，为真。
真命题有3个，选$$C$$。
3. 解析：命题为假意味着其否定为真，即$$\forall x \in \mathbf{R}, x^2 + m x + 2m - 3 \geq 0$$。
需判别式$$\Delta = m^2 - 4(2m - 3) \leq 0$$，解得$$m^2 - 8m + 12 \leq 0$$，即$$m \in [2, 6]$$，选$$A$$。
4. 解析：分析三个语句的组合。
- 若$$\oplus$$和$$\odot$$成立，即$$l \perp \alpha$$且$$l \parallel \beta$$，则$$\alpha \perp \beta$$不一定成立。
- 若$$\oplus$$和$$\odot$$成立，即$$l \perp \alpha$$且$$\alpha \perp \beta$$，则$$l \parallel \beta$$不一定成立。
- 若$$\odot$$和$$\odot$$成立，即$$l \parallel \beta$$且$$\alpha \perp \beta$$，则$$l \perp \alpha$$不一定成立。
没有必然成立的命题，选$$A$$。
5. 解析：分析命题$$p$$和$$q$$。
- $$p$$：$$x > \log_2 5 \Rightarrow x > 2$$，但$$x > 2$$不一定推出$$x > \log_2 5$$，故$$p$$为真。
- $$q$$：若$$\sin x = \frac{\sqrt{3}}{3}$$，则$$\cos 2x = 1 - 2\sin^2 x = \frac{1}{3}$$，而$$\sin^2 x = \frac{1}{3}$$，不相等，故$$q$$为假。
因此$$p \land \neg q$$为真，选$$C$$。
6. 解析：逐项分析。
- A：2是素数但不是奇数，为假。
- B：是疑问句，非命题。
- C：空间中两条直线不相交可能平行或异面，为假。
- D：$$x > 15$$的真假取决于$$x$$的值，不是确定的命题。
无正确选项，但题目要求选一个，可能是题目设计问题。
7. 解析：由题意，$$f'(1) = -2a$$，且$$f(x) = 0$$在$$[1, +\infty)$$有解。
求导得$$f'(x) = \frac{1}{x} - 2a x - b$$，由$$f'(1) = 1 - 2a - b = -2a$$，得$$b = 1$$。
设$$f(x) = 0$$有解，即$$\ln x - a x^2 - x = 0$$有解。取$$x = 1$$，得$$-a -1 = 0$$，即$$a = -1$$。
因此$$a$$的最小值为$$-1$$，选$$B$$。
8. 解析：原命题$$\forall x > 0, x^2 < 2^x$$的否定是$$\exists x_0 > 0, x_0^2 \geq 2^{x_0}$$。
原命题在某些$$x$$（如$$x=2$$）成立，但在$$x=4$$时不成立，故为假命题，选$$B$$。
9. 解析：命题$$q$$的否定是$$\exists x_0 \in \mathbf{R}, x_0^2 \leq 0$$。
当$$x_0 = 0$$时，$$x_0^2 = 0$$，故否定为真，选$$D$$。
10. 解析：全称量词命题为$$B$$和$$D$$。
- $$B$$：任意偶数的立方仍是偶数，为真。
- $$D$$：$$x = 1$$时$$x^2 = x$$，不满足$$x^2 > x$$，为假。
因此假命题是$$D$$，选$$D$$。