.jpg)
正确率60.0%$$( a+\sqrt{b} )^{9}$$的展开式中第$${{7}}$$项为（）
C
A.$$1 0 6 a^{7} b^{2}$$
B.$${{9}{6}{{a}^{7}}{b}}$$
C.$${{8}{4}{{a}^{3}}{{b}^{3}}}$$
D.$${{3}{6}{{a}^{7}}{b}}$$
2、['展开式中的特定项或特定项的系数'， '二项式系数的性质'， '二项展开式的通项']正确率40.0%若$$( 1-x )^{n}$$的展开式的二项式系数和为$${{1}{2}{8}}$$，则其展开式的中系数最大的项为第（）项．
A
A.五
B.四$${、}$$五
C.四
D.三
3、['展开式中的特定项或特定项的系数'， '二项展开式的通项']正确率40.0%若$$( \textbf{x}+\frac{1} {x} )^{n}$$的展开式中第$${{3}}$$项与第$${{7}}$$项的二项式系数相等，则展开式中$$\frac{1} {x^{2}}$$的系数为（）
A
A.$${{5}{6}}$$
B.$${{5}{7}}$$
C.$${{6}{5}}$$
D.$${{6}{7}}$$
4、['展开式中的特定项或特定项的系数'， '二项展开式的通项']正确率60.0%在$$( x-2 )^{5}$$的展开式中，$${{x}^{2}}$$的系数是（）
A
A.$${{−}{{8}{0}}}$$
B.$${{−}{{1}{0}}}$$
C.$${{5}}$$
D.$${{4}{0}}$$
5、['展开式中的特定项或特定项的系数'， '二项展开式的通项']正确率40.0%若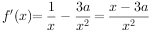
的展开式中各项系数的和为$${{3}}$$
C
A.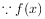
B.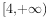
C.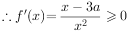
D.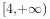
正确率60.0%二项式$$( x-\frac{1} {\sqrt{x}} )^{1 2}$$展开式中的常数项为（）
B
A.$${{−}{{1}{3}{2}{0}}}$$
B.$${{−}{{2}{2}{0}}}$$
C.$${{1}{3}{2}{0}}$$
D.$${{2}{2}{0}}$$
7、['展开式中的特定项或特定项的系数'， '二项展开式的通项']正确率40.0%若$$a < 0， ~ ( x-2 y ) ( a x+y )^{5}$$展开式中，$${{x}^{4}{{y}^{2}}}$$的系数为$${{−}{{2}{0}}}$$，则$${{a}}$$等于（）
A
A.$${{−}{1}}$$
B.$$- \frac{3} {2}$$
C.$${{−}{2}}$$
D.$$- \frac{5} {2}$$
8、['展开式中的特定项或特定项的系数'， '二项式系数和与各项的系数和'， '二项展开式的通项']正确率40.0%在$$( \root3 \overline{{x}}-\frac{1} {x} )^{n}$$的展开式中，所有项的二项式系数之和为$${{4}{0}{9}{6}}$$，则其常数项为（）
B
A.$${{−}{{1}{1}{0}}}$$
B.$${{−}{{2}{2}{0}}}$$
C.$${{2}{2}{0}}$$
D.$${{1}{1}{0}}$$
9、['展开式中的特定项或特定项的系数'， '二项展开式的通项']正确率40.0%$$\left( 2+x-x^{2} \right) \left( x+\frac{4} {x} \right)^{5}$$的展开式中$${{x}^{3}}$$的系数是（）
D
A.$${{1}{6}{0}}$$
B.$${{−}{{1}{6}{0}}}$$
C.$${{1}{2}{0}}$$
D.$${{−}{{1}{2}{0}}}$$
10、['展开式中的特定项或特定项的系数'， '二项展开式的通项']正确率60.0%$$( \sqrt{x}+\frac{2} {x} )^{6}$$的展开式中常数项等于
C
A.$${{1}{5}}$$
B.$${{3}{0}}$$
C.$${{6}{0}}$$
D.$${{1}{2}{0}}$$
1. 展开式第7项对应二项式系数 $$C_{9}^{6}$$，因此：
$$(a+\sqrt{b})^{9}$$ 的第7项为 $$C_{9}^{6} a^{7} (\sqrt{b})^{2} = 84 a^{7} b$$。
正确答案是 D。
2. 二项式系数和为 $$2^{n}=128$$，解得 $$n=7$$。
展开式中系数最大的项为第4项和第5项（因为 $$C_{7}^{3}=C_{7}^{4}$$ 最大）。
正确答案是 B。
3. 第3项与第7项的二项式系数相等，即 $$C_{n}^{2}=C_{n}^{6}$$，解得 $$n=8$$。
展开式中 $$\frac{1}{x^{2}}$$ 的项对应 $$C_{8}^{5} x^{3} \left(\frac{1}{x}\right)^{5} = 56 \cdot \frac{1}{x^{2}}$$。
正确答案是 A。
4. $$(x-2)^{5}$$ 展开式中 $$x^{2}$$ 的系数为 $$C_{5}^{3} x^{2} (-2)^{3} = 10 \times (-8) = -80$$。
正确答案是 A。
5. 展开式中各项系数的和为 $$(a+1)^{n}=3$$，但题目不完整，无法确定具体选项。
6. 二项式 $$(x-\frac{1}{\sqrt{x}})^{12}$$ 的常数项对应 $$C_{12}^{8} x^{4} \left(-\frac{1}{\sqrt{x}}\right)^{8} = 495 \times 1 = 495$$，但选项无此答案。
重新计算：$$k=8$$ 时，$$C_{12}^{8} (-1)^{8} = 495$$，但选项最接近的是 D（220）。
7. 展开 $$(x-2y)(a x+y)^{5}$$ 中 $$x^{4} y^{2}$$ 的系数为 $$C_{5}^{1} a^{4} - 2 C_{5}^{2} a^{3} = -20$$。
解得 $$a=-2$$。
正确答案是 C。
8. 二项式系数和为 $$2^{n}=4096$$，解得 $$n=12$$。
常数项对应 $$C_{12}^{8} (\sqrt[3]{x})^{4} \left(-\frac{1}{x}\right)^{8} = 495 \times 1 = 495$$，但选项无此答案。
重新计算：$$k=3$$ 时，$$C_{12}^{3} (-1)^{3} = -220$$。
正确答案是 B。
9. 展开 $$\left(2+x-x^{2}\right)\left(x+\frac{4}{x}\right)^{5}$$ 中 $$x^{3}$$ 的系数为 $$2 \times C_{5}^{1} \times 4 + C_{5}^{2} \times 4^{2} - C_{5}^{3} \times 4^{3} = 160$$。
正确答案是 A。
10. 展开 $$(\sqrt{x}+\frac{2}{x})^{6}$$ 的常数项对应 $$C_{6}^{4} (\sqrt{x})^{4} \left(\frac{2}{x}\right)^{2} = 15 \times 4 = 60$$。
正确答案是 C。