正确率40.0%已知:$$x ( x-2 )^{8}=a_{0}+a_{1} ( x-1 )+a_{2} ( x-1 )^{2}+\ldots+a_{9} ( x-1 )^{9}$$,则$${{a}_{6}{=}}$$()
A
A.$${{−}{{2}{8}}}$$
B.$${{−}{{4}{4}{8}}}$$
C.$${{1}{1}{2}}$$
D.$${{4}{4}{8}}$$
2、['展开式中的特定项或特定项的系数', '二项式定理的应用']正确率60.0%若在$$( \ensuremath{x}+1 )^{4} \begin{array} {c} {( \ensuremath{a} x-1 )} \\ \end{array}$$的展开式中,$${{x}^{4}}$$的系数为$${{1}{5}}$$,则$${{a}}$$的值为()
C
A.$${{−}{4}}$$
B.$$\frac{5} {2}$$
C.$${{4}}$$
D.$$\frac{7} {2}$$
3、['展开式中的特定项或特定项的系数', '二项式定理的应用', '二项展开式的通项']正确率60.0%在$$( \textbf{x}+\frac{1} {x^{2}} ) \setminus( \textbf{x}-2 )^{-5}$$的展开式中,$${{x}}$$的系数为()
C
A.$${{−}{{3}{2}}}$$
B.$${{−}{8}}$$
C.$${{8}}$$
D.$${{4}{8}}$$
4、['二项式定理的应用']正确率40.0%已知多项式$$( \, x-\frac{1} {x} \, ) \; \; \; ( \, x^{3}+x^{2}+x \, ) \; \;=a_{0} x^{4}+a_{1} x^{3}+a_{2} x^{2}+a_{3} x+a_{4}$$,则$$a_{1}+a_{2}=\cline{} ($$)
C
A.$${{−}{1}}$$
B.$${{0}}$$
C.$${{1}}$$
D.$${{2}}$$
5、['展开式中的特定项或特定项的系数', '二项式系数的性质', '二项式定理的应用']正确率40.0%已知:$$x \left( x-2 \right)^{8}=a_{0}+a_{1} \left( x-1 \right)+a_{2} \left( x-1 \right)^{2}+\cdots+a_{9} \left( x-1 \right)^{9}$$,则$$a_{6}=( \eta)$$
A
A.$${{−}{{2}{8}}}$$
B.$${{−}{{4}{4}{8}}}$$
C.$${{1}{1}{2}}$$
D.$${{4}{4}{8}}$$
6、['展开式中的特定项或特定项的系数', '二项式系数和与各项的系数和', '二项式定理的应用']正确率60.0% ,则
,则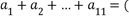
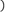
B
A.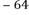
B.
C.$${{6}{4}}$$
D.$${{6}{5}}$$
7、['二项式系数和与各项的系数和', '二项式定理的应用']正确率60.0%若$$( x+1 )^{5}=a_{0}+a_{1} ( x-1 )+a_{2} ( x-1 )^{2}+\ldots+a_{5} ( x-1 )^{5}$$,则$$a_{0}=( \qquad\qquad)$$
A
A.$${{3}{2}}$$
B.$${{1}}$$
C.$${{−}{1}}$$
D.$${{−}{{3}{2}}}$$
8、['二项式系数和与各项的系数和', '二项式定理的应用', '二项展开式的通项']正确率60.0%若$$( a-3 x ) ( \sqrt{x}-\frac{1} {2 x} )^{1 0}$$的展开式中含$$x^{\frac{1} {2}}$$项的系数为$${{−}{{3}{0}}}$$,则实数$${{a}}$$的值为$${{(}{)}}$$
A
A.$${{2}}$$
B.$${{−}{2}}$$
C.$${{1}}$$
D.$${{−}{1}}$$
9、['二项式系数和与各项的系数和', '二项式定理的应用']正确率60.0%若$$\left( 1+m x \right)^{6}=a_{0}+a_{1} x+a_{2} x^{2}+\cdots+a_{6} x^{6}$$且$$a_{1}+a_{2}+\cdots+a_{6}=6 3$$,则实数$${{m}{=}{(}}$$)
C
A.$${{1}}$$
B.$${{−}{1}}$$或$${{3}}$$
C.$${{1}}$$或$${{−}{3}}$$
D.$${{−}{3}}$$
10、['二项式系数的性质', '二项式定理的应用', '二项展开式的通项']正确率60.0%$$( \textbf{x}+\frac{1} {x} ) \sp{1 0}$$的展开式中系数最大的项是()
B
A.第$${{5}}$$项
B.第$${{6}}$$项
C.第$${{5}}$$项$${、}$$第$${{6}}$$项
D.第$${{6}}$$项$${、}$$第$${{7}}$$项
1. 解析:
2. 解析:
3. 解析:
4. 解析:
5. 解析:
6. 解析:
7. 解析:
8. 解析:
9. 解析:
10. 解析:
.jpg)