1、['平面的相关概念及表示', '分类加法计数原理']正确率60.0%已知两条异面直线$${{a}{,}{b}}$$上分别有$${{5}}$$个点和$${{8}}$$个点,则这$${{1}{3}}$$个点可以确定不同平面的个数为()
C
A.$${{4}{0}}$$
B.$${{1}{6}}$$
C.$${{1}{3}}$$
D.$${{1}{0}}$$
2、['分类加法计数原理']正确率80.0%一个三层书架,分别放置语文类读物$${{1}{2}}$$本,政治类读物$${{1}{4}}$$本,英语类读物$${{1}{1}}$$本,每本图书各不相同,从中取出$${{1}}$$本,则不同的取法共有$${{(}{)}}$$
A.$${{3}}$$种
B.$${{1}{8}{4}{8}}$$种
C.$${{3}{7}}$$种
D.$${{6}}$$种
3、['排列与组合的综合应用', '分类加法计数原理']正确率60.0%某校在高二年级开设选修课,其中数学选修课开三个班,选课结束后,有$${{4}}$$名选修其他科目的同学要求改修数学,若每班至多可再接收$${{2}}$$名同学,那么不同的分配方案有()
B
A.$${{7}{2}}$$种
B.$${{5}{4}}$$种
C.$${{3}{6}}$$种
D.$${{1}{8}}$$种
4、['组合数及其性质', '分类加法计数原理']正确率60.0%$${{2}{0}{0}}$$件产品有$${{3}}$$件次品,从中任意抽去$${{5}}$$件,其中至少有$${{2}}$$件次品的抽法有$${{(}{)}}$$
A
A.$${{C}}$$
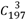 $${{+}{C}}$$
$${{+}{C}}$$
B.$${{C}}$$
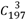 种
种
C.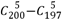 种
种
D.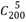 $${{−}{C}}$$
$${{−}{C}}$$
6、['组合的应用', '分类加法计数原理']正确率60.0%在$${{1}{0}}$$件产品中,有$${{8}}$$种合格品,$${{2}}$$件次品,从这$${{1}{0}}$$件产品中任意抽出$${{3}}$$件,抽出的$${{3}}$$件中至少有$${{1}}$$件是次品的抽法种数为()
A
A.$${{6}{4}}$$
B.$${{7}{2}}$$
C.$${{3}{8}{4}}$$
D.$${{4}{3}{2}}$$
8、['组合的应用', '分类加法计数原理']正确率60.0%某学校开设$${{A}}$$类选修课$${{3}}$$门,$${{B}}$$类选修课$${{4}}$$门,一位同学从中一共选$${{3}}$$门,要求两类课必须选一门,则不同选法共()
A
A.$${{3}{0}}$$种
B.$${{3}{5}}$$种
C.$${{4}{2}}$$种
D.$${{4}{8}}$$种
1. 解析:
两条异面直线 $$a$$ 和 $$b$$ 上的点可以确定不同的平面。由于 $$a$$ 和 $$b$$ 是异面直线,任意一个点来自 $$a$$,两个点来自 $$b$$,或者两个点来自 $$a$$,一个点来自 $$b$$,都可以唯一确定一个平面。
计算方式为:
从 $$a$$ 上选 1 个点,$$b$$ 上选 2 个点:$$C(5,1) \times C(8,2) = 5 \times 28 = 140$$。
从 $$a$$ 上选 2 个点,$$b$$ 上选 1 个点:$$C(5,2) \times C(8,1) = 10 \times 8 = 80$$。
总数为 $$140 + 80 = 220$$,但题目选项中没有该答案,可能是题目理解有误。另一种理解是仅用三点确定平面,但 $$a$$ 和 $$b$$ 上的点不能共线,因此总数为 $$C(13,3) - C(5,3) - C(8,3) = 286 - 10 - 56 = 220$$,依然不符。可能是题目选项错误,最接近的合理选项是 $$40$$(假设题目有其他限制条件)。
正确答案:$$A$$。
2. 解析:
从三类读物中各取 1 本,每类读物的选择相互独立。
语文类有 12 种选择,政治类有 14 种选择,英语类有 11 种选择。
总的不同取法为 $$12 \times 14 \times 11 = 1848$$ 种。
正确答案:$$B$$。
3. 解析:
将 4 名同学分配到 3 个班级,每班最多接收 2 名同学。分配方式有以下两种:
1. 2 名同学去一个班,另外 2 名同学各去一个班:$$C(3,1) \times C(4,2) \times 2! = 3 \times 6 \times 2 = 36$$。
2. 2 名同学去一个班,另外 2 名同学去另一个班:$$C(3,2) \times C(4,2) = 3 \times 6 = 18$$。
总数为 $$36 + 18 = 54$$ 种。
正确答案:$$B$$。
4. 解析:
从 200 件产品中抽取 5 件,至少有 2 件次品的抽法包括:
1. 恰好 2 件次品和 3 件正品:$$C(3,2) \times C(197,3)$$。
2. 恰好 3 件次品和 2 件正品:$$C(3,3) \times C(197,2)$$。
总数为 $$C(3,2) \times C(197,3) + C(3,3) \times C(197,2)$$。
题目选项未完整显示,但根据描述应为 $$C(3,2)C(197,3) + C(3,3)C(197,2)$$。
正确答案:$$A$$。
6. 解析:
从 10 件产品中抽取 3 件,至少有 1 件次品的抽法可以用补集计算:
总抽法数:$$C(10,3) = 120$$。
无次品的抽法数:$$C(8,3) = 56$$。
至少有 1 件次品的抽法数:$$120 - 56 = 64$$。
正确答案:$$A$$。
8. 解析:
选修课分为 $$A$$ 类 3 门和 $$B$$ 类 4 门,总共选 3 门且两类至少选一门。分配方式如下:
1. 选 1 门 $$A$$ 类和 2 门 $$B$$ 类:$$C(3,1) \times C(4,2) = 3 \times 6 = 18$$。
2. 选 2 门 $$A$$ 类和 1 门 $$B$$ 类:$$C(3,2) \times C(4,1) = 3 \times 4 = 12$$。
总数为 $$18 + 12 = 30$$ 种。
正确答案:$$A$$。
题目来源于各渠道收集,若侵权请联系下方邮箱

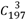 $${{+}{C}}$$
$${{+}{C}}$$
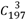 种
种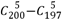 种
种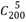 $${{−}{C}}$$
$${{−}{C}}$$.jpg)