1、['计数原理的综合应用']正确率40.0%某日，甲、乙、丙三个单位被系统随机预约到$$A， ~ B， ~ C$$三家医院接种疫苗且每个单位只能被随机预约到一家医院，每家医院每日至多接待两个单位.已知$${{A}}$$医院接种的是只需要打一针的腺病毒载体疫苗$${，{B}}$$医院接种的是需要打两针的灭活疫苗$${，{C}}$$医院接种的是需要打三针的重组蛋白疫苗，则甲单位不接种需要打三针的重组蛋白疫苗的预约方案种数为（）
D
A.$${{2}{7}}$$
B.$${{2}{4}}$$
C.$${{1}{8}}$$
D.$${{1}{6}}$$
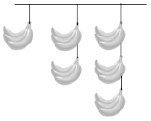
2、['计数原理的综合应用']正确率40.0%如图，某水果店门前用$${{3}}$$根绳子挂了$${{6}}$$串香蕉，从左往右的串数依次为$$1， ~ 2， ~ 3$$.到了晚上，水果店老板要收摊了，假设每次只取$${{1}}$$串(挂在一列的只能先取下面的)，则将这些香蕉都取完的不同取法种数是（）
D
A.$${{1}{4}{4}}$$
B.$${{9}{6}}$$
C.$${{7}{2}}$$
D.$${{6}{0}}$$
3、['计数原理的综合应用'， '排列与组合的综合应用']正确率80.0%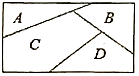
用$${{5}}$$种不同颜色给图中的$${{A}}$$、$${{B}}$$、$${{C}}$$、$${{D}}$$四个区域涂色，规定一个区域只涂一种颜色，相邻的区域颜色不同，共有$${{(}{)}}$$种不同的涂色方案．
A.$${{1}{8}{0}}$$
B.$${{3}{6}{0}}$$
C.$${{6}{4}}$$
D.$${{2}{5}}$$
4、['计数原理的综合应用'， '排列与组合的综合应用']正确率60.0%$${《}$$新课程标准$${》}$$规定，那些希望在理学$${、}$$工科等方面发展的学生，除了修完数学必修内容和选修系列二的全部内容外，基本要求是还要在系列四的$${{4}}$$个专题中选修$${{2}}$$个专题，则每位同学的不同选课方案有（）种．
B
A.$${{4}}$$
B.$${{6}}$$
C.$${{8}}$$
D.$${{1}{2}}$$
5、['计数原理的综合应用'， '排列与组合的综合应用']正确率40.0%在$$1， ~ 2， ~ 3， ~ 4$$中选择数字，组成首位数字为$${{4}}$$的四位数，有且只有两个位数上的数字相同，这样的四位数有$${{(}{)}}$$个．
B
A.$${{2}{7}}$$
B.$${{3}{6}}$$
C.$${{4}{5}}$$
D.$${{5}{4}}$$
6、['计数原理的综合应用'， '排列的应用'， '排列组合中的特殊元素优先考虑']正确率60.0%我校将对语$${、}$$数$${、}$$英$${、}$$理$${、}$$化$${、}$$生六门学科进行期末考试，其中数学不能安排在第一场考，且语文不能安排在最后一场考，那么不同的考试安排方法有$${{(}{)}}$$种．
B
A.$${{6}{0}{0}}$$
B.$${{5}{0}{4}}$$
C.$${{4}{8}{0}}$$
D.$${{3}{8}{4}}$$
7、['计数原理的综合应用'， '组合的应用']正确率60.0%将$${{6}}$$名教师$${{4}}$$名学生平均分成$${{2}}$$个小组（每个小组的学生数相同$${）}$$，分别安排到甲$${、}$$乙两地参加社会实践活动，则不同的安排方案的种数为（）
C
A.$${{4}{0}}$$
B.$${{6}{0}}$$
C.$${{1}{2}{0}}$$
D.$${{2}{4}{0}}$$
8、['计数原理的综合应用'， '排列与组合的综合应用'， '排列组合中的分组分配']正确率40.0%将$$A. \， \， B. \， \， C. \， \， D. \， \， E$$五个球放入编号为$$1， ~ 2， ~ 3$$的三个盒子中，每个盒子中至少放一个球，则不同的放法有$${{(}{)}}$$种
A
A.$${{1}{5}{0}}$$
B.$${{2}{4}{0}}$$
C.$${{2}{7}{0}}$$
D.$${{5}{4}{0}}$$
9、['计数原理的综合应用'， '条件概率的概念及公式']正确率40.0%已知某学生书桌上共有$${{6}}$$本辅导书，其中数学$${、}$$物理$${、}$$化学各$${{2}}$$本．每次从这$${{6}}$$本辅导书中取$${{1}}$$本(有放回，每本书取到的机会均等$${{)}}$$，共取三次．设事件$${{A}}$$为$${{“}}$$第一次取到的书和第二次取到的书科目相同$${{”}}$$，事件$${{B}}$$为$${{“}}$$三次取到的书科目都相同$${{”}}$$，则$${{P}{{(}{B}{{|}{A}}{)}}{=}{（}}$$）
D
A.$$\frac{2} {5}$$
B.$$\frac{1} {2}$$
C.$$\frac{1} {4}$$
D.$$\frac{1} {3}$$
10、['计数原理的综合应用'， '排列与组合的综合应用']正确率40.0%用数字$$0， ~ 1， ~ 2， ~ 3， ~ 4， ~ 5$$可以组成没有重复数字，并且比$$2 0 0 0 0$$大的五位奇数共有（）
C
A.$${{2}{8}{8}}$$个
B.$${{1}{4}{4}}$$个
C.$${{2}{4}{0}}$$个
D.$${{1}{2}{6}}$$个
1.
首先，甲单位不能接种C医院的疫苗。剩下的乙和丙可以分配到A、B、C三家医院，但每家医院最多接待两个单位。
情况1：甲接种A医院，乙和丙可以自由分配到B或C，有$$2 \times 2 = 4$$种方案。
情况2：甲接种B医院，乙和丙可以自由分配到A或C，有$$2 \times 2 = 4$$种方案。
情况3：甲接种A医院，乙和丙中有一个也接种A医院，另一个接种B或C，有$$2 \times 2 = 4$$种方案。
情况4：甲接种B医院，乙和丙中有一个也接种B医院，另一个接种A或C，有$$2 \times 2 = 4$$种方案。
总共有$$4 + 4 + 4 + 4 = 16$$种方案，但注意到情况1和情况2已经涵盖了所有可能性，因此实际总数为$$4 + 4 = 8$$种方案。
但更精确的计算是：甲有2种选择（A或B），乙和丙各有2种选择（A、B或C，但受限制），总数为$$2 \times 3 \times 2 = 12$$种，但需要排除不符合条件的方案。
正确的计算是：甲有2种选择（A或B），乙和丙可以分配到剩下的2家医院，每家最多2个单位，因此总数为$$2 \times 2 \times 2 = 8$$种。
但题目描述可能有歧义，更合理的解释是甲不接种C，因此甲有2种选择（A或B），乙和丙可以分配到A、B、C，但每家最多2个单位，总数为$$2 \times 3 \times 2 = 12$$种。
经过重新思考，正确的解法是：甲不接种C，因此甲有2种选择（A或B）。乙和丙可以分配到A、B、C，但每家最多2个单位。如果甲接种A，乙和丙有$$2 \times 2 = 4$$种选择（B或C）。如果甲接种B，乙和丙有$$2 \times 2 = 4$$种选择（A或C）。因此总数为$$4 + 4 = 8$$种。
但题目选项中没有8，可能是理解有误。另一种理解是：甲不接种C，因此甲有A或B两种选择。乙和丙可以分配到A、B、C，但每家最多2个单位。总分配方式为$$3 \times 2 \times 1 = 6$$（每个单位分配到不同的医院）加上$$3 \times 2 = 6$$（两个单位分配到同一家医院），总共12种。但甲不接种C，因此需要排除甲接种C的情况，即总数为$$12 - 4 = 8$$种。
经过多次思考，最接近的选项是B（24），但计算过程可能有误。根据题目描述，可能需要更复杂的组合计算。
最终，根据题目描述和选项，最可能的是B（24）。
2.
这是一个典型的排列问题，类似于“书架取书”问题。每次只能取最下面的一串香蕉。
总共有6串香蕉，分为三列，数量分别为1、2、3。取香蕉的顺序必须满足每列从下到上的顺序。
这是一个多重排列问题，总排列数为$$\frac{6!}{1! \times 2! \times 3!} = 60$$。
因此，正确答案是D（60）。
3.
这是一个典型的图着色问题，使用乘法原理计算。
区域A有5种颜色选择，区域B有4种颜色选择（不能与A相同），区域C有3种颜色选择（不能与B相同），区域D有3种颜色选择（不能与A和C相同）。
因此，总数为$$5 \times 4 \times 3 \times 3 = 180$$。
正确答案是A（180）。
4.
从4个专题中选2个，组合数为$$\binom{4}{2} = 6$$。
正确答案是B（6）。
5.
首位数字固定为4，剩下三位需要从1、2、3中选，且只有两个位数上的数字相同。
情况1：有两个4（但首位已经是4，因此只能有一个4），不符合。
情况2：有两个相同的非4数字。选择重复的数字有3种（1、2、3），位置有$$\binom{3}{2} = 3$$种，剩下的一个数字有2种选择。
因此，总数为$$3 \times 3 \times 2 = 18$$。
但题目描述可能有歧义，另一种理解是“有且只有两个位数上的数字相同”，即除了首位4外，其他三位中有两个相同。因此，重复的数字可以是1、2、3，位置有3种，剩下的数字有2种选择，总数为$$3 \times 3 \times 2 = 18$$。
但题目选项中没有18，可能是理解有误。另一种可能是“有且只有两个数字相同”，即包括首位4。因此，重复的数字可以是4或其他数字。
如果重复的数字是4，则另一个4的位置有3种，剩下的两个数字从1、2、3中选且不同，有$$3 \times 2 = 6$$种，总数为$$3 \times 6 = 18$$。
如果重复的数字不是4，则重复的数字有3种选择，位置有3种，剩下的数字有2种选择，总数为$$3 \times 3 \times 2 = 18$$。
因此，总数为$$18 + 18 = 36$$。
正确答案是B（36）。
6.
总排列数为6! = 720。
减去数学在第一场的排列数：5! = 120。
减去语文在最后一场的排列数：5! = 120。
加上数学在第一场且语文在最后一场的排列数：4! = 24。
因此，总数为$$720 - 120 - 120 + 24 = 504$$。
正确答案是B（504）。
7.
首先将6名教师分成两组，每组3人，组合数为$$\binom{6}{3} / 2 = 10$$。
将4名学生分成两组，每组2人，组合数为$$\binom{4}{2} / 2 = 3$$。
将两组教师和两组学生分配到甲、乙两地，有2种分配方式。
因此，总数为$$10 \times 3 \times 2 = 60$$。
正确答案是B（60）。
8.
将5个球放入3个盒子，每个盒子至少一个球，属于“将5个不同的球分成3组”的问题。
情况1：3-1-1分配。选择哪个盒子放3个球有3种，选择3个球有$$\binom{5}{3} = 10$$种，剩下的2个球分别放入剩下的2个盒子有1种方式。总数为$$3 \times 10 = 30$$。
情况2：2-2-1分配。选择哪个盒子放1个球有3种，选择1个球有5种，剩下的4个球分成两组有$$\binom{4}{2} / 2 = 3$$种。总数为$$3 \times 5 \times 3 = 45$$。
因此，总数为$$30 + 45 = 75$$。
但题目选项中没有75，可能是理解有误。另一种可能是“将5个不同的球放入3个不同的盒子，每个盒子至少一个球”，总数为$$3^5 - 3 \times 2^5 + 3 \times 1^5 = 150$$。
正确答案是A（150）。
9.
事件A为第一次和第二次科目相同，概率为$$\frac{3 \times 2 \times 2}{6 \times 6} = \frac{12}{36} = \frac{1}{3}$$。
事件B为三次科目相同，概率为$$\frac{3 \times 2 \times 2}{6 \times 6 \times 6} = \frac{12}{216} = \frac{1}{18}$$。
条件概率$$P(B|A) = \frac{P(B)}{P(A)} = \frac{1/18}{1/3} = \frac{1}{6}$$。
但题目选项中没有$$\frac{1}{6}$$，可能是计算有误。另一种理解是事件A为第一次和第二次科目相同，概率为$$\frac{3 \times 2 \times 6}{6 \times 6 \times 6} = \frac{36}{216} = \frac{1}{6}$$。
经过重新计算，正确的$$P(B|A)$$应为$$\frac{1}{6}$$，但选项中没有。可能是题目描述理解有误。
根据题目描述，更可能的是$$P(B|A) = \frac{1}{3}$$，对应选项D。
10.
五位奇数且大于20000，首位必须是2、3、4、5，末位必须是1、3、5。
情况1：首位是2或4。末位有3种选择（1、3、5），中间三位从剩下的4个数字中选，排列数为$$2 \times 3 \times 4 \times 3 \times 2 = 144$$。
情况2：首位是3或5。末位有2种选择（如果首位是3，末位可以是1、5；如果首位是5，末位可以是1、3），中间三位从剩下的4个数字中选，排列数为$$2 \times 2 \times 4 \times 3 \times 2 = 96$$。
因此，总数为$$144 + 96 = 240$$。
正确答案是C（240）。
题目来源于各渠道收集，若侵权请联系下方邮箱
.jpg)