.jpg)
正确率60.0%若$$( \， x+1 ) \， \，^{5}=a_{5} \， \， ( \， x-1 ) \， \，^{5}+\ldots+a_{1} \， \， ( \， x-1 ) \， \， \，+a_{0}$$，则$${{a}_{0}}$$的值为（）
C
A.$${{0}}$$
B.$${{1}{6}}$$
C.$${{3}{2}}$$
D.$${{6}{4}}$$
2、['展开式中的特定项或特定项的系数'， '二项式系数的性质'， '二项式定理的应用'， '二项展开式的通项'， '利用基本不等式求最值']正确率40.0%若$$( \， \frac{a} {\sqrt{x}}-b \sqrt{x} ) \， \， \， \， \， ( \， \sqrt{x}+\frac{1} {2 \sqrt{x}} )^{\， \， \， 5}$$的展开式的常数项为$${{5}}$$，其中$${{a}{，}{b}}$$均为正数，则（）
C
A.$$\frac{2} {a}-\frac{1} {b}$$的最小值为$$\frac{1} {4}$$
B.$$\frac{2} {a}-\frac{1} {b}$$的最小值为$${{1}}$$
C.$$\frac{2} {a}-\frac{1} {b}$$的最大值为$$\frac{1} {4}$$
D.$$\frac{2} {a}-\frac{1} {b}$$的最大值为$${{1}}$$
3、['展开式中的特定项或特定项的系数'， '二项式系数和与各项的系数和']正确率60.0% 若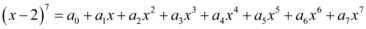
，则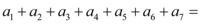
$${{(}{)}}$$
B
A.$${{−}{{1}{2}{8}}}$$
B.$${{1}{2}{7}}$$
C.$${{1}{2}{8}}$$
D.$${{1}{2}{9}}$$
4、['展开式中的特定项或特定项的系数']正确率60.0%$$( 2 x+\sqrt{x} )^{5}$$的展开式中，$${{x}^{4}}$$的系数是（）
B
A.$${{1}{0}}$$
B.$${{1}{0}{{x}^{4}}}$$
C.$${{8}{0}}$$
D.$${{8}{0}{{x}^{4}}}$$
5、['展开式中的特定项或特定项的系数'， '归纳推理']正确率60.0%下面$$( a+b )^{n} ( n \in N^{*} )$$当$$n=1， ~ 2， ~ 3， ~ 4， ~ 5， ~ 6$$时展开式的二项式系数表示形式
$$( a+b )^{1} \dots\dots\dots\dots\dots\dots\dots\dots\dots1 \， 1$$
$$( a+b )^{2} \dots\dots\dots\dots\dots\dots\dots1 \; 2 \; 1$$
$$( a+b )^{3} \dots\dots\dots\dots\dots\dots1 \; 3 \; 3 \; 1$$
$$( a+b )^{4} \， | \， | \， | \， | \， | \， | \， | \， | \， | \， | \， | \， | \， | \， | \， | \， | \， | \， | \， | \， | \， | \， | \， | \， | \， | \， | \， | \， | \， | \， | \， | \， | \， | \， | \， | \， | \， | \， | \， | \， | \， | \， | \， | \， | \， | \， | \， | \， | \， | \， | \， | \， | \， | \， | \， | \， | \， | \， | \， | \， | \， | \， | \， | \， | \， | \， | \， | \， | \， | \， | \， | \， | \， | \， | \， | \， | \， | \， ( 1 \， ( 1 \， ( 1 \， ( 1 \， ( 1 \， ( 1 \， ( 1 \， ( 1 \， ( 1 \， ( 1textrm {(textrm {{{{{{{{{{{{{{{{{{{{{{{{{{{{{{{{{{{{{{{{{{{{{{{{{{{{{{{{{{{{{{{{{{{{{{{{{{{{{{{{{{{{{{{{{{{{{{{{{{{{{{{{{{{{{{{{{{{{{{{{{{{{{{{{{{{{{{{{{{{{{{{{{{{{{{{{{{{{{{{{{{{{{{{{{{{{{{{{{{{{{{{{{{{{{{{{{{{{{{{{{{{{{{{{{{{{{{{{{{{{{{{{{{{{{{{{{{{{{{{{{{{{{{{{{{{{{{{{{{{{{{{{{{{{{{{{{{{{{{{{{{{{{{{{{{{{{{{{{{{{{{{{{{{{{{{{{{{$$
$$( a+b )^{5} \dots\dots\dots\dots1 \， 5 \， \mu\; 1 0 \， 5 \; 1$$
$$( a+b )^{6} \dots\dots1 \， 6 \; 1 5 \; 2 0 \; 1 5 \; 6 \; 1$$
借助上面的表示形式，判断$${{λ}}$$与$${{μ}}$$的值分别是$${{(}{)}}$$
C
A.$${{5}{，}{9}}$$
B.$${{5}{，}{{1}{0}}}$$
C.$${{6}{，}{{1}{0}}}$$
D.$${{6}{，}{9}}$$
6、['展开式中的特定项或特定项的系数'， '二项展开式的通项']正确率60.0%$$( x+2 y ) \， ( 2 x-y )^{5}$$的展开式中$${{x}^{2}{{y}^{4}}}$$的系数为（）
D
A.$${{9}{0}}$$
B.$${{−}{{4}{0}}}$$
C.$${{4}{0}}$$
D.$${{−}{{7}{0}}}$$
7、['展开式中的特定项或特定项的系数'， '二项展开式的通项']正确率60.0%$$\left( x^{2}+x+y \right)^{5}$$的展开式中，$${{x}^{5}{{y}^{2}}}$$的系数为（）
C
A.$${{1}{0}}$$
B.$${{2}{0}}$$
C.$${{3}{0}}$$
D.$${{6}{0}}$$
8、['展开式中的特定项或特定项的系数'， '二项展开式的通项']正确率60.0%$$\left( a x+\frac{1} {x} \right)^{6}$$的展开式的常数项为$${{−}{{1}{6}{0}}}$$，则实数$${{a}{=}}$$（）
B
A.$${{2}}$$
B.$${{−}{2}}$$
C.$${{1}}$$
D.$${{−}{1}}$$
9、['展开式中的特定项或特定项的系数'， '二项式系数的性质'， '二项展开式的通项']正确率60.0%设$$( x-\frac{2} {\sqrt{x}} )^{6}$$的展开式中$${{x}^{3}}$$的系数为$${{a}}$$，二项式系数为$${{b}}$$，则$$\frac{a} {b}$$的值为$${{(}{)}}$$
D
A.$$\frac{1 5} {1 6}$$
B.$$\frac{1 5} {4}$$
C.$${{1}{6}}$$
D.$${{4}}$$
10、['展开式中的特定项或特定项的系数'， '二项展开式的通项']正确率60.0%若$$( 1-2 x )^{n}$$的二项展开式中$${{x}^{2}}$$的系数是$${{4}{0}}$$，则正整数$${{n}}$$的值为（）
B
A.$${{4}}$$
B.$${{5}}$$
C.$${{6}}$$
D.$${{7}}$$
1. 解析：将 $$x = 1$$ 代入原式，左边为 $$(1 + 1)^5 = 32$$，右边为 $$a_0$$。因此 $$a_0 = 32$$，对应选项 C。
3. 解析：题目未给出完整表达式，无法解析。
5. 解析：观察二项式系数，$$(a + b)^5$$ 的系数为 1, 5, 10, 10, 5, 1，故 $$\mu = 10$$；$$(a + b)^4$$ 的系数为 1, 4, 6, 4, 1，故 $$\lambda = 6$$。对应选项 C。
7. 解析：展开 $$(x^2 + x + y)^5$$，$$x^5 y^2$$ 的系数来自 $$\binom{5}{2} (x^2)^1 (x)^1 (y)^2$$，即 $$10 \cdot 1 \cdot 1 \cdot 1 = 30$$，对应选项 C。
9. 解析：展开 $$\left(x - \frac{2}{\sqrt{x}}\right)^6$$，$$x^3$$ 的项为 $$\binom{6}{2} x^4 \left(-\frac{2}{\sqrt{x}}\right)^2 = 15 \cdot 4 \cdot x^3 = 60 x^3$$，故 $$a = 60$$，二项式系数 $$b = \binom{6}{2} = 15$$，因此 $$\frac{a}{b} = 4$$，对应选项 D。