正确率40.0%如图,准备用$${{4}}$$种不同的颜色给$$a, ~ b, ~ c, ~ d, ~ e$$五块区域涂色,要求每个区域随机用$${{1}}$$种颜色涂色,且相邻区域(有公共边的)所涂颜色不能相同,则不同的涂色方法的种数为()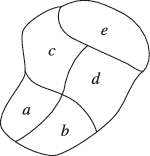
C
A.$${{9}{6}}$$
B.$${{1}{1}{4}}$$
C.$${{1}{6}{8}}$$
D.$${{2}{4}{0}}$$
2、['排列组合中的涂色问题']正确率60.0%如图,图案共分$${{9}}$$个区域,有$${{6}}$$种不同颜色的涂料可供涂色,每个区域只能涂一种颜色的涂料,其中$${{2}}$$和$${{9}}$$同色、$${{3}}$$和$${{6}}$$同色、$${{4}}$$和$${{7}}$$同色、$${{5}}$$和$${{8}}$$同色,且相邻区域的颜色不相同,则涂色方法有()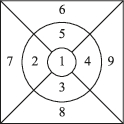
B
A.$${{3}{6}{0}}$$种
B.$${{7}{2}{0}}$$种
C.$${{7}{8}{0}}$$种
D.$${{8}{4}{0}}$$种
3、['排列组合中的涂色问题']正确率60.0%如图,一环形花坛分成$$A, ~ B, ~ C, ~ D$$四块,现有$${{4}}$$种不同的花供选种,要求在每块里种$${{1}}$$种花,且相邻的两块种不同的花,则不同的种法种数为()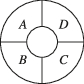
B
A.$${{9}{6}}$$
B.$${{8}{4}}$$
C.$${{6}{0}}$$
D.$${{4}{8}}$$
4、['排列组合中的涂色问题']正确率40.0%现有$${{5}}$$种不同的颜色,要给如图所示的$${{5}}$$个区域涂色,要求有公共边界的两块不能用同一种颜色,则不同的涂色方法共有()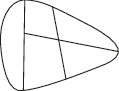
B
A.$${{4}{2}{0}}$$种
B.$${{7}{8}{0}}$$种
C.$${{5}{4}{0}}$$种
D.$${{4}{8}{0}}$$种
5、['计数原理的综合应用', '排列与组合的综合应用', '排列组合中的涂色问题']正确率40.0%正方体六个面上分别标有$${{A}}$$、$${{B}}$$、$${{C}}$$、$${{D}}$$、$${{E}}$$、$${{F}}$$六个字母,现用$${{5}}$$种不同的颜色给此正方体六个面染色,要求有公共棱的面不能染同一种颜色,则不同的染色方案有()种.
D
A.$${{4}{2}{0}}$$
B.$${{6}{0}{0}}$$
C.$${{7}{2}{0}}$$
D.$${{7}{8}{0}}$$
6、['排列组合中的涂色问题']正确率40.0%用四种不同的颜色给三棱柱$$A B C-A_{1} B_{1} C_{1}$$六个顶点涂色,要求每个点涂一种颜色,且每条棱的两个端点涂不同的颜色,则不同的涂色方法有()种.
D
A.$${{2}{8}{8}}$$
B.$${{2}{4}{0}}$$
C.$${{1}{6}{8}}$$
D.$${{2}{6}{4}}$$
7、['排列与组合的综合应用', '排列组合中的涂色问题']正确率40.0%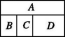 现有$${{4}}$$
现有$${{4}}$$
C
A.$${{2}{4}}$$
B.$${{3}{0}}$$
C.$${{4}{8}}$$
D.$${{5}{0}}$$
8、['排列组合中的涂色问题']正确率40.0%如图,有一种游戏画板,要求参与者用六种颜色给画板涂色,这六种颜色分别为红色$${、}$$黄色$${{1}{、}}$$黄色$${{2}{、}}$$黄色$${{3}{、}}$$金色$${{1}{、}}$$金色$${{2}}$$,其中黄色$${{1}{、}}$$黄色$${{2}{、}}$$黄色$${{3}}$$是三种不同的颜色,金色$${{1}{、}}$$金色$${{2}}$$是两种不同的颜色,要求红色不在两端,黄色$${{1}{、}}$$黄色$${{2}{、}}$$黄色$${{3}}$$有且仅有两种相邻,则不同的涂色方案有()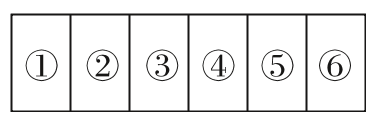
D
A.$${{1}{2}{0}}$$种
B.$${{2}{4}{0}}$$种
C.$${{1}{4}{4}}$$种
D.$${{2}{8}{8}}$$种
9、['排列组合中的涂色问题']正确率60.0%如图所示的几何体是由一个三棱锥$$P-A B C$$与三棱柱$$A B C-A_{1} B_{1} C_{1}$$组合而成,现用$${{3}}$$种不同颜色对这个几何体的表面涂色(底面$${{A}_{1}{{B}_{1}}{{C}_{1}}}$$不涂色$${)}$$,要求相邻的面均不同色,则不同的涂色方案共有()
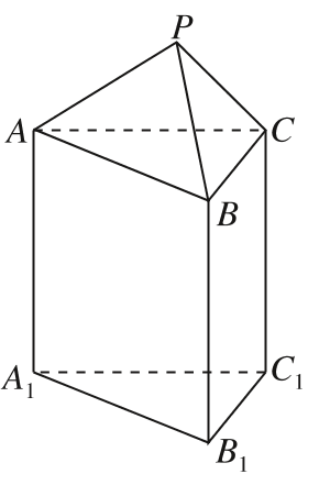
C
A.$${{3}{6}}$$种
B.$${{2}{4}}$$种
C.$${{1}{2}}$$种
D.$${{9}}$$种
10、['排列组合中的涂色问题', '分步乘法计数原理', '分类加法计数原理']正确率40.0%用$${{6}}$$种不同的颜色给图中$$A, ~ B, ~ C, ~ D 4$$块区域涂色,若相邻区域不能涂同一种颜色,则不同的涂色方法共有()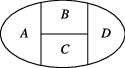
B
A.$${{2}{4}{0}}$$种
B.$${{4}{8}{0}}$$种
C.$${{5}{2}{0}}$$种
D.$${{1}{2}{0}}$$种
1. 解析:
2. 解析:
3. 解析:
4. 解析:
5. 解析:
6. 解析:
7. 解析:
8. 解析:
9. 解析:
10. 解析:
.jpg)