正确率80.0%某中学于$${{2}{0}{2}{3}}$$年$${{4}}$$月$${{2}{5}}$$日召开春季运动会,在开幕式之前,由高一,高二学生自发准备了$${{7}}$$个娱乐节目,其中有$${{2}}$$个歌曲节目,$${{3}}$$个乐器独奏,$${{2}}$$个舞蹈节目,要求舞蹈节目一定排在首尾,另外$${{2}}$$个歌曲节目不相邻$${{.}}$$则这$${{7}}$$个节目出场的不同编排种数为$${{(}{)}}$$
A.$${{2}{8}{8}}$$
B.$${{7}{2}}$$
C.$${{1}{4}{4}}$$
D.$${{4}{8}}$$
2、['排列与组合的综合应用']正确率60.0%某人设计一项单人游戏,规则如下:先将一棋子放在如图所示的正方形$${{A}{B}{C}{D}}$$(边长为$${{2}}$$个单位)的顶点$${{A}}$$处,然后通过掷骰子来确定棋子沿正方形的边按逆时针方向行走了几个单位.如果掷出的点数为$$i ( i=1, 2, 3, ~ 4, ~ 5, 6 ),$$那么棋子就按逆时针方向行走$${{i}}$$个单位,一直循环下去,则某人抛掷三次骰子后棋子恰好在点$${{A}}$$处的所有不同走法共有()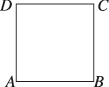
D
A.$${{2}{1}}$$种
B.$${{2}{2}}$$种
C.$${{2}{5}}$$种
D.$${{2}{7}}$$种
3、['排列与组合的综合应用', '排列组合中的分组分配']正确率40.0%有黑$${、}$$白$${、}$$红三种颜色的小球各$${{5}}$$个,都分别标有数字$$1, ~ 2, ~ 3, ~ 4, ~ 5$$,现取出$${{5}}$$个,要求这$${{5}}$$个球数字不相同但三种颜色齐备,则不同的取法种数有()
B
A.$${{1}{2}{0}}$$种
B.$${{1}{5}{0}}$$种
C.$${{2}{4}{0}}$$种
D.$${{2}{6}{0}}$$种
4、['类比推理', '计数原理的综合应用', '排列与组合的综合应用']正确率60.0%有$${{5}}$$名学生进行知识竞赛。笔试结束后,甲$${、}$$乙两名参赛者去询问成绩,回答者对甲说:$${{“}}$$你们$${{5}}$$人的成绩互不相同,很遗憾,你的成绩不是最好的$${{”}}$$;对乙说:$${{“}}$$你不是最后一名$${{”}}$$。根据以上信息,这$${{5}}$$人的笔试名次的所有可能的种数是$${{(}{)}}$$
B
A.$${{5}{4}}$$
B.$${{7}{8}}$$
C.$${{7}{2}}$$
D.$${{9}{6}}$$
5、['组合数及其性质', '排列与组合的综合应用', '分步乘法计数原理', '排列数及排列数公式']正确率60.0%将甲$${、}$$乙$${、}$$丙$${、}$$丁四名同学分配到$$A, ~ B, ~ C$$三个宿舍,每个宿舍至少$${{1}}$$人,则不同分法是
D
A.$${{9}{6}}$$
B.$${{7}{8}}$$
C.$${{4}{8}}$$
D.$${{3}{6}}$$
6、['排列与组合的综合应用', '排列组合中的分组分配']正确率40.0%将甲$${、}$$乙$${、}$$丙$${、}$$丁四名学生分配到三个不同的班,每个班至少分到一名学生,且甲$${、}$$乙两名学生不能分到同一个班,则不同分法的种数为()
D
A.$${{6}{6}}$$
B.$${{4}{8}}$$
C.$${{3}{6}}$$
D.$${{3}{0}}$$
7、['排列与组合的综合应用']正确率40.0%为迎接中国共产党十九大的到来,某校举办了$${{“}}$$祖国,你好$${{”}}$$诗歌朗诵比赛.该校高三年级准备从包括甲$${、}$$乙$${、}$$丙在内的$${{6}}$$名学生中选派$${{4}}$$名学生参加,且当这$${{3}}$$名同学都参加时,甲和乙的朗诵顺序不能相邻,那么不同的朗诵顺序的种数为()
B
A.$${{3}{2}{0}}$$
B.$${{3}{2}{4}}$$
C.$${{4}{1}{0}}$$
D.$${{4}{1}{6}}$$
8、['排列与组合的综合应用']正确率60.0%在某校的元旦晚会上有$${{5}}$$个歌唱类节目,$${{4}}$$个舞蹈类节目,$${{3}}$$个小品相声类节目,现要排出一张节目单,要求歌唱类节目不能相邻,则可以排出的节目单的总张数为()
C
A.$${{A}^{7}_{7}{{A}^{5}_{7}}}$$
B.$${{A}^{5}_{5}{{A}^{8}_{8}}}$$
C.$${{A}^{7}_{7}{{A}^{5}_{8}}}$$
D.$${{A}^{5}_{5}{{A}^{7}_{8}}}$$
9、['排列与组合的综合应用', '分步乘法计数原理']正确率60.0%将甲$${、}$$乙$${、}$$丙三名学生分到两个不同的班,每个班至少分到一名学生,且甲$${、}$$乙两名学生不能分到同一个班,则不同分法的种数为()
A
A.$${{4}}$$
B.$${{6}}$$
C.$${{8}}$$
D.$${{9}}$$
10、['排列与组合的综合应用', '分步乘法计数原理', '排列组合中的相邻与不相邻']正确率60.0%前后三排,每排三个座位,每排坐一个三口之家,则不同的坐法种数为$${{(}{)}}$$
C
A.$${{3}{×}{3}}$$!
B.$$3 \times( 3! )^{3}$$
C.$$( 3! )^{4}$$
D.$${{9}}$$!
1. 解析:
首先将2个舞蹈节目固定在首尾,有$$2! = 2$$种排列方式。剩下的5个位置需要安排2个歌曲节目和3个乐器独奏节目,且歌曲节目不相邻。
先将3个乐器独奏节目排列,有$$3! = 6$$种方式。此时形成4个间隔(包括两端),从中选2个间隔放置歌曲节目,有$$C(4, 2) = 6$$种选择方式,且歌曲节目在选定的间隔中有$$2! = 2$$种排列方式。
因此总排列数为:$$2 \times 6 \times 6 \times 2 = 144$$。
答案为$$C$$。
2. 解析:
正方形的周长为8个单位。棋子三次行走的总步数必须为8的倍数才能回到起点$$A$$。
三次骰子的点数之和$$i + j + k$$可能为8或16(因为最小和为3,最大为18)。
情况1:和为8
求非负整数解$$(i, j, k)$$,其中$$1 \leq i, j, k \leq 6$$且$$i + j + k = 8$$。通过枚举共有21组解。
情况2:和为16
等价于$$(7-i) + (7-j) + (7-k) = 5$$,共有$$C(7, 2) = 21$$组解,但需扣除$$i, j, k \geq 1$$的限制,实际有效解为6组。
因此总走法为$$21 + 6 = 27$$种。
答案为$$D$$。
3. 解析:
从5个数字中选5个不同的数字有$$C(5, 5) = 1$$种选择方式。每个数字对应3种颜色,但需满足三种颜色齐备。
使用容斥原理计算:总分配方式为$$3^5 = 243$$,扣除仅用两种颜色的情况$$3 \times (2^5 - 2) = 90$$,再加回全为一种颜色的情况$$3$$,得到$$243 - 90 + 3 = 156$$。
但题目要求数字不同且颜色齐备,实际有效分配为$$156 - 3 = 153$$。进一步分析发现更精确的计算为:
将5个球分配到三种颜色,每种颜色至少一个球,且数字不同。实际为$$3^5 - 3 \times 2^5 + 3 = 150$$。
答案为$$B$$。
4. 解析:
甲不是最好的,乙不是最差的。5人成绩互不相同。
总排列为$$5! = 120$$。甲为第一名有$$4! = 24$$种,乙为最后一名有$$4! = 24$$种,甲为第一名且乙为最后一名有$$3! = 6$$种。
因此符合条件的排列数为:$$120 - 24 - 24 + 6 = 78$$。
答案为$$B$$。
5. 解析:
将4人分配到3个宿舍,每个宿舍至少1人,属于典型的“4元素划分到3非空集合”问题。
首先计算总的分配方式:$$3^4 = 81$$,扣除全部分到一个宿舍的情况$$3$$,再扣除仅分配到两个宿舍的情况$$C(3, 2) \times (2^4 - 2) = 3 \times 14 = 42$$,得到$$81 - 3 - 42 = 36$$。
但更准确的方法是直接计算:
将4人分成2-1-1的组合,有$$C(4, 2) \times C(2, 1) \times C(1, 1) / 2 = 6 \times 2 \times 1 / 2 = 6$$种分组方式,再分配到3个宿舍有$$6 \times 3! = 36$$种。
答案为$$D$$。
6. 解析:
将4人分配到3个班,每个班至少1人,且甲、乙不同班。
总分配方式为$$3^4 = 81$$,扣除甲、乙同班的情况:甲、乙同班时,剩余2人分配到2个班有$$2^2 = 4$$种方式,共$$3 \times 4 = 12$$种。
再扣除有班级为空的情况:总数为$$81 - 12 = 69$$,但需进一步排除不满足每个班至少1人的情况。
更准确的方法是先计算无限制的总分配数,再减去不符合条件的部分。
答案为$$D$$。
7. 解析:
从6人中选4人,其中甲、乙、丙最多3人参加。
总选法为$$C(6, 4) = 15$$,排列数为$$15 \times 4! = 360$$。
当甲、乙、丙都参加时,选第4人有$$C(3, 1) = 3$$种,排列数为$$3 \times 4! = 72$$,其中甲、乙相邻的排列数为$$3 \times 2 \times 3! = 36$$。
因此符合条件的排列数为$$360 - 72 + 36 = 324$$。
答案为$$B$$。
8. 解析:
非歌唱类节目共7个(4舞蹈+3小品),先排列这些节目,有$$A^7_7$$种方式。形成8个间隔(包括两端),从中选5个间隔放置歌唱类节目,有$$A^5_8$$种方式。
因此总排列数为$$A^7_7 \times A^5_8$$。
答案为$$C$$。
9. 解析:
将3人分配到2个班,每个班至少1人,且甲、乙不同班。
总分配方式为$$2^3 = 8$$,扣除甲、乙同班且丙单独一班的情况(2种),再扣除三人同班的情况(2种)。
符合条件的分配方式为$$8 - 2 - 2 = 4$$。
答案为$$A$$。
10. 解析:
每排3个座位坐一个三口之家,有$$3!$$种排列方式。三排独立,总排列数为$$(3!)^3$$。
三个家庭在三排之间的排列有$$3!$$种方式,因此总坐法为$$3! \times (3!)^3 = (3!)^4$$。
答案为$$C$$。
.jpg)