正确率80.0%学校要求学生从物理、历史、化学、生物、政治、地理这$${{6}}$$科中选$${{3}}$$科参加考试,规定先从物理和历史中任选$${{1}}$$科,然后从其他$${{4}}$$科中任选$${{2}}$$科,则不同的选法种数为()
B
A.$${{5}}$$
B.$${{1}{2}}$$
C.$${{2}{0}}$$
D.120
2、['组合的应用']正确率60.0%甲、乙、丙三地任意两地之间有直达的火车,相互之间距离均不相等且无通票,则车票票价的种数是()
C
A.$${{1}}$$
B.$${{2}}$$
C.$${{3}}$$
D.$${{6}}$$
3、['古典概型的概率计算公式', '互斥事件的概率加法公式', '组合的应用', '概率的基本性质']正确率60.0%北斗七星分别为天枢、天璇、天玑、天权、玉衡、开阳、摇光,其中玉衡最亮,天权最暗.一名天文爱好者从七颗星中随机选两颗进行观测,则玉衡和天权至少有一颗被选中的概率为()
B
A.$$\frac{1 0} {2 1}$$
B.$$\frac{1 1} {2 1}$$
C.$$\frac{1 1} {4 2}$$
D.$$\frac{5} {2 1}$$
4、['古典概型的概率计算公式', '组合的应用', '分类加法计数原理']正确率40.0%某公司准备招聘一批员工,有$${{2}{0}}$$人经过初试,其中有$${{5}}$$人是与公司所需专业不对口,其余都是对口专业,在不知道面试者专业情况下,现依次选取$${{2}}$$人进行第二次面试,则选取的第二人与公司所需专业不对口的概率是()
C
A.$$\frac{5} {1 9}$$
B.$$\frac{1} {1 9}$$
C.$$\frac{1} {4}$$
D.$$\frac{1} {2}$$
5、['古典概型的概率计算公式', '古典概型的应用', '组合的应用']正确率40.0%某课题小组共有$${{1}{5}}$$名同学,其中有$${{7}}$$名男生,现从中任意选出$${{1}{0}}$$人,用$${{X}}$$表示这$${{1}{0}}$$人中男生的人数,则下列概率等于$$\frac{C_{7}^{4} \, C_{8}^{6}} {C_{1 5}^{1 0}}$$的是()
B
A.$$P \left( X \leqslant4 \right)$$
B.$$P \left( \right. X=4 )$$
C.$$P \left( X \leq6 \right)$$
D.$$P \left( \right. X=6 )$$
6、['古典概型的概率计算公式', '组合的应用']正确率40.0%某舞台灯光设备有一种$${{2}{5}}$$头$${{L}{E}{D}}$$矩阵灯$${{(}}$$如图所示$${{)}}$$,有$${{3}}$$头$${{L}{E}{D}}$$灯出现故障,假设每头$${{L}{E}{D}}$$灯出现故障都是等可能的,则这$${{3}}$$头故障$${{L}{E}{D}}$$灯两两不在同一行也不在同一列的概率为()
C
A.$$\frac{4} {2 3}$$
B.$$\frac{5} {2 3}$$
C.$$\frac{6} {2 3}$$
D.$$\frac{7} {2 3}$$
7、['排列与组合的综合应用', '组合的应用', '排列的应用', '分类加法计数原理']正确率60.0%将小亮等$${{5}}$$名同学全部安排到$$A. ~ B. ~ C. ~ D$$四个社区参加社区活动,每个社区至少安排一人,则小亮在$${{A}}$$社区的安排方案共有()
D
A.$${{2}{4}}$$种
B.$${{3}{6}}$$种
C.$${{4}{8}}$$种
D.$${{6}{0}}$$种
8、['组合的应用', '排列组合中的涂色问题', '分步乘法计数原理']正确率60.0%小明要给图中的矩形$$A. ~ B. ~ C. ~ D$$涂色,有$${{4}}$$种不同的颜色可供选择,若要求相邻的矩形涂色不同,则不同的涂法有()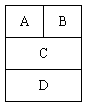
A
A.$${{7}{2}}$$种
B.$${{4}{8}}$$种
C.$${{2}{4}}$$种
D.$${{1}{2}}$$种
9、['组合数及其性质', '组合的应用']正确率60.0%计算:$$C_{2 0 1 9}^{2 0 1 8}=( \textsubscript{\Lambda} )$$
B
A.$${{2}{0}{1}{8}}$$
B.$${{2}{0}{1}{9}}$$
C.$${{4}{0}{3}{7}}$$
D.$${{1}}$$
10、['古典概型的概率计算公式', '组合的应用']正确率60.0%现有$${{4}}$$本不同的书平均分给两名同学,则语文书$${、}$$数学书恰好分给一位同学的概率为()
B
A.$$\frac{1} {2}$$
B.$$\frac{1} {3}$$
C.$$\frac{1} {6}$$
D.$$\frac1 {1 2}$$
1. 第一步从物理和历史中选1科,有$$C_2^1 = 2$$种选择;第二步从剩下的4科中选2科,有$$C_4^2 = 6$$种选择。根据乘法原理,总的不同选法种数为$$2 \times 6 = 12$$种,对应选项B。
2. 甲、乙、丙三地两两之间有直达火车,共$$C_3^2 = 3$$种不同的路线。由于距离不等且无通票,每种路线的票价不同,因此票价种数为3,对应选项C。
3. 从7颗星中选2颗的总方法数为$$C_7^2 = 21$$。玉衡和天权至少选中一颗的补集是两颗都没选中,方法数为$$C_5^2 = 10$$,因此所求概率为$$1 - \frac{10}{21} = \frac{11}{21}$$,对应选项B。
4. 20人中有5人不对口,15人对口。无论第一次选的是对口还是不对口,第二次选不对口的概率均为$$\frac{5}{20} = \frac{1}{4}$$,对应选项C。
5. 题目给出的概率表达式$$\frac{C_7^4 C_8^6}{C_{15}^{10}}$$表示从7名男生中选4人、8名女生中选6人的概率,即$$P(X=4)$$,对应选项B。
6. 25头LED灯排成5×5矩阵,选3头故障灯的总方法数为$$C_{25}^3 = 2300$$。要求3头故障灯不同行不同列,方法数为$$5 \times 4 \times 3 \times C_5^3 = 600$$(先选3行3列再排列)。因此概率为$$\frac{600}{2300} = \frac{6}{23}$$,对应选项C。
7. 将5人分配到4个社区,每个社区至少1人,有两种情况:(1) 一个社区2人,其余1人;(2) 一个社区3人,其余1人。但题目要求小亮在A社区,因此只需考虑剩余4人的分配。若A社区有2人(小亮+1人),方法数为$$C_4^1 \times 3! = 24$$;若A社区仅小亮1人,方法数为$$C_4^2 \times 2 \times 2! = 24$$。总方案数为$$24 + 24 = 48$$,对应选项C。
8. 矩形涂色问题:假设矩形排列为A-B-C-D,A有4种选择,B有3种(不同于A),C有2种(不同于B),D有2种(不同于C)。因此总涂法为$$4 \times 3 \times 2 \times 2 = 48$$,对应选项B。
9. 组合数性质:$$C_{2019}^{2018} = C_{2019}^1 = 2019$$,对应选项B。
10. 4本书平均分给2人,总方法数为$$C_4^2 = 6$$。语文书和数学书分给同一人的方法数为2(全给甲或全给乙),因此概率为$$\frac{2}{6} = \frac{1}{3}$$,对应选项B。
.jpg)