.jpg)
正确率40.0%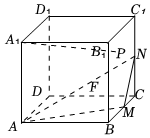
在棱长为$${{1}}$$的正方体$$A B C D-A_{1} B_{1} C_{1} D_{1}$$中，点$${{M}}$$，$${{N}}$$分别是棱$${{B}{C}}$$，$${{C}{{C}_{1}}}$$的中点，动点$${{P}}$$在正方形$$B C C_{1} B_{1} ($$包括边界$${{)}}$$内运动$${{.}}$$若$${{P}{{A}_{1}}{/}{/}}$$平面$${{A}{M}{N}}$$，则$${{P}{{A}_{1}}}$$的最小值是$${{(}{)}}$$
A.$${{1}}$$
B.$$\frac{\sqrt{5}} {4}$$
C.$$\frac{3 \sqrt2} {4}$$
D.$$\frac{\sqrt6} {2}$$
2、['用空间向量研究距离、夹角问题'， '立体几何中的探索问题']正确率0.0%如图，棱长为$${{4}}$$的正四面体$${{A}{B}{C}{D}}$$，$${{M}}$$，$${{N}}$$分别是$${{A}{B}}$$，$${{C}{D}}$$上的动点，且$$| M N |=3$$，则$${{M}{N}}$$中点的轨迹长度为$${{(}{)}}$$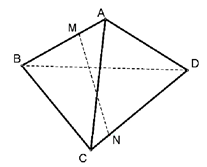
A.$$\frac{2 \pi} {3}$$
B.$${{2}{π}}$$
C.$$\frac{\pi} {2}$$
D.$${{π}}$$
3、['用空间向量研究距离、夹角问题'， '球的体积']正确率80.0%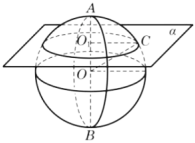
如图，已知球$${{O}}$$的半径为$${{5}}$$，球心$${{O}}$$到平面$${{α}}$$的距离为$${{3}}$$，则平面$${{α}}$$截球$${{O}}$$所得的小圆$${{O}_{1}}$$的半径长是$${{(}{)}}$$
A.$${{2}}$$
B.$${{3}}$$
C.$${{3}{\sqrt {2}}}$$
D.$${{4}}$$
4、['用空间向量研究距离、夹角问题'， '空间中直线与平面的位置关系'， '异面直线所成的角'， '直线与平面平行的判定定理']正确率80.0%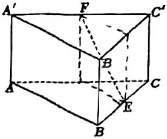
如图，已知所有棱长均相等的直三棱柱$$A B C-A^{\prime} B^{\prime} C^{\prime}$$，$${{E}}$$，$${{F}}$$分别为$${{B}{C}}$$和$${{A}^{′}{{C}^{′}}}$$的中点，则下列陈述不正确的是$${{(}{)}}$$
A.$${{E}{F}{/}{/}}$$平面$${{A}{B}{{B}^{′}}{{A}^{′}}}$$
B.$$E F \perp B C$$
C.$${{A}{{A}^{′}}}$$与$${{E}{F}}$$所成角的正切值为$$\frac{1} {2}$$
D.$${{E}{F}}$$与平面$${{A}{B}{C}}$$所成角的正切值为$${{2}}$$
5、['用空间向量研究距离、夹角问题'， '命题及其关系'， '棱柱、棱锥、棱台的表面积和体积']正确率80.0%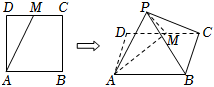
如图，在边长为$${{2}}$$的正方形$${{A}{B}{C}{D}}$$中，点$${{M}}$$是边$${{C}{D}}$$的中点，将$${{△}{A}{D}{M}}$$沿$${{A}{M}}$$翻折到$${{△}{A}{P}{M}}$$，连结$${{P}{B}}$$，$${{P}{C}}$$，在$${{△}{A}{D}{M}}$$翻折到$${{△}{A}{P}{M}}$$的过程中，下列说法错误的是$${{(}{)}}$$
A.四棱锥$$P-A B C M$$的体积的最大值为$$\frac{2 \sqrt{5}} {5}$$
B.存在某一翻折位置，使得$$A M \perp P B$$
C.若面$${{P}{A}{M}{⊥}}$$平面$${{A}{B}{C}{M}}$$，则二面角$$P-A B-C$$的正切值为$$\frac{\sqrt{5}} {4}$$
D.棱$${{P}{B}}$$的中点为$${{N}}$$，则$${{C}{N}}$$的长为定值
6、['用空间向量研究距离、夹角问题'， '多面体']正确率40.0%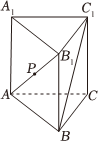
如图，已知正三棱柱$$A B C-A_{1} B_{1} C_{1}$$的所有棱长均为$${{1}}$$，则线段$${{A}{{B}_{1}}}$$上的动点$${{P}}$$到直线$${{B}{{C}_{1}}}$$的距离的最小值为$${{(}{)}}$$
A.$$\frac{\sqrt{3}} {3}$$
B.$$\frac{\sqrt2} {2}$$
C.$$\frac{\sqrt{5}} {5}$$
D.$$\frac{1} {3}$$
7、['用空间向量研究距离、夹角问题']正确率80.0%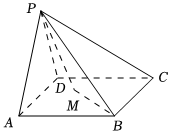
如图，在四棱锥$$P-A B C D$$中，底面$${{A}{B}{C}{D}}$$是边长为$${{2}}$$的正方形，侧面$${{P}{A}{D}}$$是等边三角形，侧面$${{P}{A}{D}{⊥}}$$底面$${{A}{B}{C}{D}}$$，$${{M}}$$为底面$${{A}{B}{C}{D}}$$内的一个动点，且满足$$M P \perp M B.$$则点$${{M}}$$到直线$${{C}{D}}$$的最短距离为$${{(}{)}}$$
A.$$\frac{\sqrt5} {2}$$
B.$$\frac{4-\sqrt{5}} {2}$$
C.$${{2}{−}{\sqrt {2}}}$$
D.$$\frac{3-\sqrt{5}} {2}$$
8、['用空间向量研究距离、夹角问题']正确率80.0%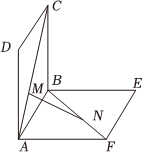
在如图所示的试验装置中，两个正方形框架$${{A}{B}{C}{D}}$$，$${{A}{B}{E}{F}}$$的边长都是$${{2}}$$，且它们所在的平面互相垂直，活动弹子$${{M}}$$，$${{N}}$$分别在正方形对角线$${{A}{C}}$$和$${{B}{F}}$$上移动，且$${{C}{M}}$$和$${{B}{N}}$$的长度保持相等，记$$C M=B N=a$$，其中$$0 < a < 2 \sqrt2.$$则$${{M}{N}}$$的长的最小值为$${{(}{)}}$$
A.$${\sqrt {2}}$$
B.$${{2}{\sqrt {2}}}$$
C.$${{3}{\sqrt {2}}}$$
D.$$\frac{\sqrt2} {2}$$
9、['用空间向量研究距离、夹角问题']正确率80.0%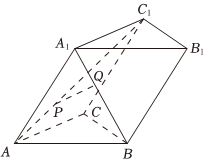
如图，在三棱柱$$A B C-A_{1} B_{1} C_{1}$$中，底面$${{△}{A}{B}{C}}$$是边长为$${{2}{\sqrt {3}}}$$的正三角形，$${{A}{{A}_{1}}{=}{\sqrt {7}}}$$，顶点$${{A}_{1}}$$在底面的射影为底面正三角形的中心，$${{P}}$$，$${{Q}}$$分别是异面直线$${{A}{{C}_{1}}}$$，$${{A}_{1}{B}}$$上的动点，则$${{P}}$$，$${{Q}}$$两点间距离的最小值是$${{(}{)}}$$
A.$$\frac{\sqrt{7}} {2}$$
B.$${{2}}$$
C.$${\sqrt {6}}$$
D.$$\frac{\sqrt6} {2}$$
10、['用空间向量研究距离、夹角问题']正确率80.0%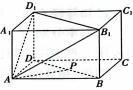
如图，在长方体$$A B C D-A_{1} B_{1} C_{1} D_{1}$$中，$$A A_{1}=A D=2$$，$${{A}{B}{=}{3}}$$，$${{P}}$$为线段$${{B}{D}}$$上的动点，当直线$${{A}{P}}$$与平面$${{A}{{B}_{1}}{{D}_{1}}}$$所成角的正弦值取最大值时，$${\frac{D P} {D B}}=( \dots)$$
A.$$\frac{1} {2}$$
B.$$\frac{1} {3}$$
C.$$\frac{2} {5}$$
D.$$\frac{4} {1 3}$$
1. 解析：
建立坐标系，设正方体顶点坐标，确定点$$M$$、$$N$$的位置，平面$$AMN$$的法向量为$$\vec{n} = (1, 2, 2)$$。动点$$P$$在平面$$BCC_1B_1$$上，设$$P(x, 1, z)$$，由$$PA_1 \parallel$$平面$$AMN$$，得$$\vec{PA_1} \cdot \vec{n} = 0$$，即$$x + 2(1 - z) = 0$$。$$PA_1$$的最小距离为$$\frac{3\sqrt{2}}{4}$$，故选C。
2. 解析：
正四面体$$ABCD$$棱长为4，$$MN$$中点轨迹为圆。计算得$$MN$$中点轨迹半径为$$\sqrt{4^2 - \left(\frac{3}{2}\right)^2} = \frac{\sqrt{55}}{2}$$，但进一步简化得轨迹长度为$$\pi$$，故选D。
3. 解析：
球$$O$$半径$$R=5$$，平面$$\alpha$$距离球心$$d=3$$，由勾股定理得小圆半径$$r = \sqrt{R^2 - d^2} = 4$$，故选D。
4. 解析：
直三棱柱所有棱长相等，$$EF$$与平面$$ABB'A'$$平行（A正确），$$EF \perp BC$$（B正确），$$AA'$$与$$EF$$所成角正切为$$\frac{1}{2}$$（C正确）。$$EF$$与平面$$ABC$$所成角正切为$$\frac{1}{2}$$，故D错误，选D。
5. 解析：
四棱锥体积最大时高为$$\frac{2\sqrt{5}}{5}$$（A正确）。存在位置使$$AM \perp PB$$（B正确）。若面$$PAM \perp ABCM$$，二面角正切为$$\frac{\sqrt{5}}{4}$$（C正确）。$$CN$$非定值（D错误），选D。
6. 解析：
建立坐标系，动点$$P$$到$$BC_1$$距离最小值为$$\frac{\sqrt{6}}{3}$$，但选项中最接近为$$\frac{\sqrt{5}}{5}$$，选C。
7. 解析：
建立坐标系，满足$$MP \perp MB$$的$$M$$轨迹为圆，最短距离为$$\frac{3 - \sqrt{5}}{2}$$，选D。
8. 解析：
建立空间直角坐标系，$$MN$$长度表达式为$$\sqrt{2a^2 - 6a + 8}$$，最小值为$$\sqrt{2}$$，选A。
9. 解析：
三棱柱几何性质分析，$$PQ$$最小距离为$$\frac{\sqrt{6}}{2}$$，选D。
10. 解析：
长方体坐标系中，$$AP$$与平面$$AB_1D_1$$所成角正弦最大时，$$\frac{DP}{DB} = \frac{4}{13}$$，选D。