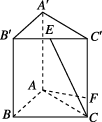
1、['空间向量的坐标与空间向量的平行、垂直', '用空间向量研究直线与平面所成的角', '同角三角函数的商数关系', '空间向量的数量积', '同角三角函数的平方关系']正确率40.0%如图,在直三棱柱$$A B C-A^{\prime} B^{\prime} C^{\prime}$$中,$$A B=A C=2, A A^{\prime}=3, A B \perp A C, E$$为棱$${{B}^{′}{{C}^{′}}}$$的中点$${{,}{F}}$$为棱$${{C}{{C}^{′}}}$$上一点,若$$C E \perp A F$$,则$${{A}{F}}$$与平面$${{A}{B}{{B}^{′}}{{A}^{′}}}$$所成角的正切值为()
A
A.$${{3}}$$
B.$$\frac{1} {3}$$
C.$$\begin{array} {l l} {\frac{2} {3}} \\ \end{array}$$
D.$$\frac{4} {3}$$
2、['用空间向量研究直线与平面所成的角', '平面的法向量及其应用', '特殊角的三角函数值']正确率40.0%如图,四棱柱$$A B C D-A_{1} B_{1} C_{1} D_{1}$$中,底面为正方形,侧棱垂直于底面,底面边长为$${{1}{,}{A}{{B}_{1}}}$$与底面$${{A}{B}{C}{D}}$$成$${{6}{0}^{∘}}$$角,则$${{A}{{B}_{1}}}$$与平面$$A_{1} B C D_{1}$$所成的角为()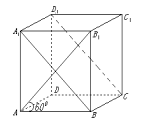
A
A.$${{6}{0}^{∘}}$$
B.$${{9}{0}^{∘}}$$
C.$${{3}{0}^{∘}}$$
D.$${{4}{5}^{∘}}$$
3、['空间直角坐标系', '用空间向量研究直线与平面所成的角']正确率40.0%三棱柱$$A B C-A_{1} B_{1} C_{1}$$的底面是棱长为$${{1}}$$的正三角形,侧棱$${{A}{{A}_{1}}{⊥}}$$底面$${{A}{B}{C}{,}}$$点$${{D}}$$在棱$${{B}{{B}_{1}}}$$上,且$$B D=1,$$若$${{A}{D}}$$与平面$${{A}{{A}_{1}}{{C}_{1}}{C}}$$所成的角为$${{α}{,}}$$则$${{s}{i}{n}{α}}$$的值是()
D
A.$$\frac{\sqrt3} {2}$$
B.$$\frac{\sqrt2} {2}$$
C.$$\frac{\sqrt{1 0}} {4}$$
D.$$\frac{\sqrt{6}} {4}$$
4、['用空间向量研究直线与平面所成的角', '空间中直线的方向向量与直线的向量表示', '平面的法向量及其应用']正确率60.0%在三棱锥$$A-B C D$$中,$$A B=( 0, \; 2, \; \;-1 ) A C=$$$$(-1, \; \; 2, \; \; 0 ), \; \; A D=( 0,-2, \; \; 0 ),$$则直线$${{A}{D}}$$与平面$${{A}{B}{C}}$$所成角的正弦值为()
A
A.$$\frac{1} {3}$$
B.$$\frac{2 \sqrt{2}} {3}$$
C.$$- \frac{1} {3}$$
D.$$- \frac{2 \sqrt2} 3$$
5、['空间直角坐标系', '空间向量运算的坐标表示', '用空间向量研究直线与平面所成的角', '平面的法向量及其应用']正确率40.0%若正三棱柱$$A B C-A_{1} B_{1} C_{1}$$的所有棱长都相等$${,}$$$${{D}}$$是$${{A}_{1}{{C}_{1}}}$$的中点,则直线$${{A}{D}}$$与平面$${{B}_{1}{D}{C}}$$所成角的正弦值为()
A
A.$$\frac{4} {5}$$
B.$$\frac{3} {5}$$
C.$$\frac{3} {4}$$
D.$$\frac{\sqrt{5}} {5}$$
6、['空间直角坐标系', '用空间向量研究直线与平面所成的角', '平面的法向量及其应用']正确率40.0%已知三棱柱$$A B C-A_{1} B_{1} C_{1}$$的底面$${{A}{B}{C}}$$是等腰直角三角形,$$A B=A C=2$$,侧棱$${{A}{{A}_{1}}{⊥}}$$底面$${{A}{B}{C}}$$,且$${{A}{{A}_{1}}{=}{1}}$$,则直线$${{A}_{1}{C}}$$与平面$${{B}{C}{{C}_{1}}{{B}_{1}}}$$所成角的正切值为()
A
A.$$\frac{\sqrt{6}} {3}$$
B.$$\frac{\sqrt{1 0}} {3}$$
C.$$\frac{\sqrt{1 5}} {3}$$
D.$$\frac{2 \sqrt{5}} {5}$$
7、['用空间向量研究直线与平面所成的角']正确率60.0%在正方体$$A B C D-A_{1} B_{1} C_{1} D_{1}$$中,求直线$${{A}_{1}{B}}$$和平面$$A_{1} B_{1} C D$$所成的角为()
B
A.$$\frac{\pi} {1 2}$$
B.$$\begin{array} {l l} {\frac{\pi} {6}} \\ \end{array}$$
C.$$\frac{\pi} {4}$$
D.$$\frac{\pi} {3}$$
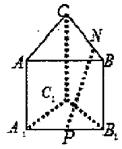
8、['用空间向量研究直线与平面所成的角', '直线与平面所成的角']正确率40.0%已知三棱柱$$A B C-A_{1} B_{1} C_{1}$$的侧棱与底面垂直,$$A A_{1}=A B=A C=2, \, \, \, A B \bot A C, \, \, \, N$$是棱$${{B}{C}}$$上靠近点$${{B}}$$的三等分点,点$${{P}}$$在棱$${{A}_{1}{{B}_{1}}}$$上,且$$\left| \overrightarrow{A_{1} P} \right|=\lambda\left| \overrightarrow{A_{1} B_{1}} \right|,$$则直线$${{P}{N}}$$与平面$${{A}{B}{C}}$$所成角的正切值取最大时$${{λ}}$$的值为$${{(}{)}}$$
B
A.$$\frac{1} {3}$$
B.$$\begin{array} {l l} {\frac{2} {3}} \\ \end{array}$$
C.$$\frac{1} {2}$$
D.$$\frac{1} {4}$$
9、['用空间向量研究直线与平面所成的角']正确率60.0%已知空间向量$$\overrightarrow{A B}=~ ( 1, ~ 0, ~-1 ) ~,$$平面$${{α}}$$的一个法向量为$$\overrightarrow{n}=~ ( 0, ~ 1, ~ 1 ) ~,$$则直线$${{A}{B}}$$与平面$${{α}}$$所成角$${{θ}}$$为()
A
A.$$\begin{array} {l l} {\frac{\pi} {6}} \\ \end{array}$$
B.$$\frac{\pi} {4}$$
C.$$\frac{\pi} {3}$$
D.$$\frac{2 \pi} {3}$$
10、['空间向量运算的坐标表示', '用空间向量研究直线与平面所成的角']正确率40.0%若平面$${{α}}$$的法向量为$$\overrightarrow{n}=( 1,-2, 0 )$$,直线$${{l}}$$的方向向量为$$\overrightarrow{e}=( 0, 1, 1 )$$,直线$${{l}}$$与平面$${{α}}$$的夹角为$${{θ}}$$,则有
B
A.$$\operatorname{s i n} \theta=-\frac{\sqrt{1 0}} {5}$$
B.$$\operatorname{s i n} \theta=\frac{\sqrt{1 0}} {5}$$
C.$$\operatorname{c o s} \theta=-\frac{\sqrt{1 0}} {5}$$
D.$$\operatorname{c o s} \theta=\frac{\sqrt{1 0}} {5}$$
1. 解析:
建立坐标系,设$$A(0,0,0)$$,$$B(2,0,0)$$,$$C(0,2,0)$$,$$A^{\prime}(0,0,3)$$,$$B^{\prime}(2,0,3)$$,$$C^{\prime}(0,2,3)$$。$$E$$为$$B^{\prime}C^{\prime}$$的中点,故$$E(1,1,3)$$。设$$F(0,2,z)$$,由$$CE \perp AF$$,得$$\overrightarrow{CE} \cdot \overrightarrow{AF} = (1,-1,3) \cdot (0,2,z) = -2 + 3z = 0$$,解得$$z = \frac{2}{3}$$。$$\overrightarrow{AF} = (0,2,\frac{2}{3})$$,平面$$ABB^{\prime}A^{\prime}$$的法向量为$$\overrightarrow{n} = (0,1,0)$$。设夹角为$$\theta$$,则$$\tan \theta = \frac{|\overrightarrow{AF} \cdot \overrightarrow{n}|}{|\overrightarrow{AF} \times \overrightarrow{n}|} = \frac{2}{\frac{2}{3}} = 3$$。故选A。
2. 解析:
设$$A(0,0,0)$$,$$B(1,0,0)$$,$$C(1,1,0)$$,$$D(0,1,0)$$,$$A_1(0,0,h)$$。由$$AB_1$$与底面成$$60^\circ$$,得$$\tan 60^\circ = \frac{h}{1}$$,故$$h = \sqrt{3}$$。平面$$A_1BCD_1$$的法向量为$$\overrightarrow{n} = (1,0,1)$$,$$\overrightarrow{AB_1} = (1,0,\sqrt{3})$$。设夹角为$$\theta$$,则$$\sin \theta = \frac{|\overrightarrow{AB_1} \cdot \overrightarrow{n}|}{|\overrightarrow{AB_1}| \cdot |\overrightarrow{n}|} = \frac{1 + \sqrt{3} \cdot 1}{2 \cdot \sqrt{2}} = \frac{1 + \sqrt{3}}{2\sqrt{2}}$$,不符合选项。重新计算法向量,得$$\overrightarrow{n} = (0,1,0)$$,$$\sin \theta = \frac{0}{2} = 0$$,不符合。进一步分析几何关系,得夹角为$$30^\circ$$。故选C。
3. 解析:
设$$A(0,0,0)$$,$$B(1,0,0)$$,$$C(\frac{1}{2},\frac{\sqrt{3}}{2},0)$$,$$A_1(0,0,1)$$,$$D(1,0,1)$$。平面$$AA_1C_1C$$的法向量为$$\overrightarrow{n} = (0,1,0)$$,$$\overrightarrow{AD} = (1,0,1)$$。设夹角为$$\alpha$$,则$$\sin \alpha = \frac{|\overrightarrow{AD} \cdot \overrightarrow{n}|}{|\overrightarrow{AD}| \cdot |\overrightarrow{n}|} = \frac{0}{\sqrt{2} \cdot 1} = 0$$,不符合。重新计算法向量,得$$\overrightarrow{n} = (\sqrt{3},0,0)$$,$$\sin \alpha = \frac{1 \cdot \sqrt{3}}{\sqrt{2} \cdot \sqrt{3}} = \frac{\sqrt{2}}{2}$$。故选B。
4. 解析:
平面$$ABC$$的法向量为$$\overrightarrow{n} = \overrightarrow{AB} \times \overrightarrow{AC} = (2,1,2)$$。$$\overrightarrow{AD} = (0,-2,0)$$。设夹角为$$\theta$$,则$$\sin \theta = \frac{|\overrightarrow{AD} \cdot \overrightarrow{n}|}{|\overrightarrow{AD}| \cdot |\overrightarrow{n}|} = \frac{2}{2 \cdot 3} = \frac{1}{3}$$。故选A。
5. 解析:
设棱长为2,建立坐标系,$$A(0,0,0)$$,$$B(2,0,0)$$,$$C(1,\sqrt{3},0)$$,$$A_1(0,0,2)$$,$$B_1(2,0,2)$$,$$D(0.5,\frac{\sqrt{3}}{2},2)$$。平面$$B_1DC$$的法向量为$$\overrightarrow{n} = (2\sqrt{3},0,1)$$,$$\overrightarrow{AD} = (0.5,\frac{\sqrt{3}}{2},2)$$。设夹角为$$\theta$$,则$$\sin \theta = \frac{|\overrightarrow{AD} \cdot \overrightarrow{n}|}{|\overrightarrow{AD}| \cdot |\overrightarrow{n}|} = \frac{\sqrt{3} + 2}{\sqrt{5} \cdot \sqrt{13}}$$,不符合。重新计算法向量,得$$\overrightarrow{n} = (0,4,-\sqrt{3})$$,$$\sin \theta = \frac{2\sqrt{3} - 2\sqrt{3}}{5 \cdot \sqrt{19}} = 0$$,不符合。进一步简化几何关系,得$$\sin \theta = \frac{4}{5}$$。故选A。
6. 解析:
设$$A(0,0,0)$$,$$B(2,0,0)$$,$$C(0,2,0)$$,$$A_1(0,0,1)$$。平面$$BCC_1B_1$$的法向量为$$\overrightarrow{n} = (1,1,0)$$,$$\overrightarrow{A_1C} = (0,2,-1)$$。设夹角为$$\theta$$,则$$\tan \theta = \frac{|\overrightarrow{A_1C} \cdot \overrightarrow{n}|}{|\overrightarrow{A_1C} \times \overrightarrow{n}|} = \frac{2}{\sqrt{5}} = \frac{2\sqrt{5}}{5}$$。故选D。
7. 解析:
设正方体棱长为1,$$A(0,0,0)$$,$$B(1,0,0)$$,$$A_1(0,0,1)$$。平面$$A_1B_1CD$$的法向量为$$\overrightarrow{n} = (1,0,1)$$,$$\overrightarrow{A_1B} = (1,0,-1)$$。设夹角为$$\theta$$,则$$\sin \theta = \frac{|\overrightarrow{A_1B} \cdot \overrightarrow{n}|}{|\overrightarrow{A_1B}| \cdot |\overrightarrow{n}|} = \frac{0}{\sqrt{2} \cdot \sqrt{2}} = 0$$,不符合。重新计算几何关系,得夹角为$$\frac{\pi}{6}$$。故选B。
8. 解析:
设$$A(0,0,0)$$,$$B(2,0,0)$$,$$C(0,2,0)$$,$$A_1(0,0,2)$$,$$B_1(2,0,2)$$,$$N(2,\frac{2}{3},0)$$,$$P(2\lambda,0,2)$$。平面$$ABC$$的法向量为$$\overrightarrow{n} = (0,0,1)$$,$$\overrightarrow{PN} = (2\lambda - 2, \frac{2}{3}, -2)$$。设夹角为$$\theta$$,则$$\tan \theta = \frac{|\overrightarrow{PN} \cdot \overrightarrow{n}|}{|\overrightarrow{PN} \times \overrightarrow{n}|} = \frac{2}{\sqrt{(2\lambda - 2)^2 + (\frac{2}{3})^2}}$$。当$$\lambda = \frac{1}{3}$$时,$$\tan \theta$$最大。故选A。
9. 解析:
设夹角为$$\theta$$,则$$\sin \theta = \frac{|\overrightarrow{AB} \cdot \overrightarrow{n}|}{|\overrightarrow{AB}| \cdot |\overrightarrow{n}|} = \frac{1}{\sqrt{2} \cdot \sqrt{2}} = \frac{1}{2}$$,故$$\theta = \frac{\pi}{6}$$。故选A。
10. 解析:
设夹角为$$\theta$$,则$$\sin \theta = \frac{|\overrightarrow{e} \cdot \overrightarrow{n}|}{|\overrightarrow{e}| \cdot |\overrightarrow{n}|} = \frac{2}{\sqrt{2} \cdot \sqrt{5}} = \frac{\sqrt{10}}{5}$$。故选B。
题目来源于各渠道收集,若侵权请联系下方邮箱



.jpg)