正确率19.999999999999996%在正三棱柱$$A B C-A_{1} B_{1} C_{1}$$中$$, \, \, \, A B=2, \, \, \, A A_{1}=3,$$点$${{D}}$$为$${{B}{C}}$$的中点,点$${{E}}$$为线段$${{A}_{1}{C}}$$上的点,且满足$$A_{1} E=m E C ( m > 0 ),$$当平面$${{E}{A}{D}}$$与平面$${{A}{D}{C}}$$夹角的正切值为$$\begin{array} {l l} {\frac{3} {2}} \\ \end{array}$$时,实数$${{m}}$$的值为()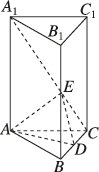
C
A.$$\frac{1} {2}$$
B.$${{1}}$$
C.$${{2}}$$
D.$${{3}}$$
2、['用空间向量研究两个平面所成的角']正确率40.0%已知两个平面的一个法向量分别是$$\boldsymbol{m}=( 1, ~ ~ 2, ~-1 ), ~ ~ \boldsymbol{n}=( 1, ~-1, ~ 0 ),$$则这两个平面的夹角的余弦值为()
D
A.$$- \frac{\sqrt{3}} {6}$$或$$\frac{\sqrt{3}} {6}$$
B.$$\frac{\sqrt{3}} {3}$$
C.$$- \frac{\sqrt{3}} {6}$$
D.$$\frac{\sqrt{3}} {6}$$
3、['用空间向量研究两个平面所成的角']正确率60.0%已知两平面的法向量分别为$$\boldsymbol{m}=( 0, ~ ~ 1, ~ ~ 0 ), ~ ~ \boldsymbol{n}=( 0, ~ ~ 1, ~ ~ 1 ),$$则两平面的夹角为()
C
A.$${{3}{0}^{∘}}$$
B.$${{1}{3}{5}^{∘}}$$
C.$${{4}{5}^{∘}}$$
D.$${{9}{0}^{∘}}$$
4、['用空间向量研究两个平面所成的角']正确率40.0%如图所示,在正四面体$$D-A B C$$中$$, ~ P, ~ Q, ~ R$$分别为$$A B, ~ B C, ~ C A$$上的点,$$A P=P B, \, \, \, \frac{B Q} {Q C}=\frac{C R} {R A}=2.$$ 分别记二面角$$D-P R-Q, ~ D-P Q-R, ~ D-Q R-P$$ 的平面角为$$\alpha, ~ \beta, ~ \gamma,$$ 则$$\alpha, ~ \beta, ~ \gamma$$ 的大小关系为( )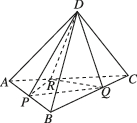
B
A.$$\alpha< \beta< \gamma$$
B.$$\alpha< \gamma< \beta$$
C.$$\beta< \alpha< \gamma$$
D.$$\gamma< \alpha< \beta$$
5、['用空间向量研究两个平面所成的角']正确率60.0%已知两平面的法向量分别为$$\boldsymbol{m}=( 0, ~ ~ 1, ~ ~ 0 ), ~ ~ \boldsymbol{n}=( 0, ~ ~ 1, ~ ~ 1 ),$$则两平面夹角为()
A
A.$${{4}{5}^{∘}}$$
B.$${{1}{3}{5}^{∘}}$$
C.$${{4}{5}^{∘}}$$或$${{1}{3}{5}^{∘}}$$
D.$${{9}{0}^{∘}}$$
6、['用空间向量研究两个平面所成的角']正确率40.0%如图,在棱长都相等的正三棱柱$$A B C-A_{1} B_{1} C_{1}$$中$${,{D}}$$是棱$${{C}{{C}_{1}}}$$的中点$${,{E}}$$是棱$${{A}{{A}_{1}}}$$上的动点.设$$A E=x,$$随着$${{x}}$$的增大,平面$${{B}{D}{E}}$$与平面$${{A}{B}{C}}$$的夹角()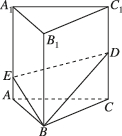
D
A.增大
B.先增大再减小
C.减小
D.先减小再增大
7、['用空间向量研究两个平面所成的角']正确率60.0%正$${{△}{A}{B}{C}}$$与正$${{△}{B}{C}{D}}$$所在平面垂直,则二面角$$A-B D-C$$的正弦值为$${{(}{)}}$$
C
A.$$\frac{\sqrt{5}} {5}$$
B.$$\frac{\sqrt{3}} {3}$$
C.$$\frac{2 \sqrt{5}} {5}$$
D.$$\frac{\sqrt{6}} {3}$$
8、['二面角', '用空间向量研究两个平面所成的角']正确率40.0%已知在正方体$$A B C D-A_{1} B_{1} C_{1} D_{1}$$中,$${{M}}$$为棱$${{A}{{A}_{1}}}$$的中点,则平面$${{D}_{1}{B}{{C}_{1}}}$$与平面$${{M}{B}{C}}$$所成锐二面角的余弦值为()
D
A.$$\frac{\sqrt{1 5}} {5}$$
B.$$\frac{\sqrt{3}} {3}$$
C.$$\frac{\sqrt{2 1 0}} {1 5}$$
D.$$\frac{\sqrt{1 0}} {5}$$
9、['空间中直线与直线的位置关系', '空间中平面与平面的位置关系', '二面角', '平面的法向量及其应用', '用空间向量研究两个平面所成的角']正确率19.999999999999996%如图,已知正四面体$$D-A B C ~ ($$所有棱长均相等的三棱锥$$) \, \,, \, \, P, \, \, \, Q, \, \, \, R$$分别为$$A B, ~ B C, ~ C A$$上的点,$$A P=P B, \, \, \, \frac{B Q} {Q C}=\frac{C R} {R A}=2$$,分别记二面角$$D-P R-Q, ~ D-P Q-R, ~ D-Q R-P$$的平面角为$$\alpha, ~ \beta, ~ \gamma,$$则()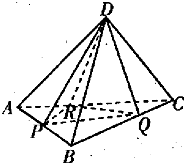
B
A.$$\gamma< \alpha< \beta$$
B.$$\alpha< \gamma< \beta$$
C.$$\alpha< \beta< \gamma$$
D.$$\beta< \gamma< \alpha$$
10、['空间向量的坐标与空间向量的平行、垂直', '空间中平面与平面的位置关系', '二面角', '空间向量的数量积', '用空间向量研究两个平面所成的角', '空间向量数量积的性质']正确率60.0%二面角的棱上有$${{A}{、}{B}}$$两点,直线$$A C \backslash\ B D$$分别在这个二面角的两个半平面内,且都垂直于$${{A}{B}}$$.已知$$A B=4, \, \, \, A C=6, \, \, \, B D=8, \, \, \, C D=2 \sqrt{1 7}$$,则该二面角的大小为$${{(}{)}}$$
C
A.$${{1}{5}{0}^{∘}}$$
B.$${{4}{5}^{∘}}$$
C.$${{6}{0}^{∘}}$$
D.$${{1}{2}{0}^{∘}}$$
以下是各题的详细解析:
1. 解析:
建立坐标系,设点 $$A(0,0,0)$$,$$B(2,0,0)$$,$$C(1,\sqrt{3},0)$$,$$A_1(0,0,3)$$,$$D$$ 为 $$BC$$ 中点,坐标为 $$(1.5, \sqrt{3}/2, 0)$$。
由 $$A_1E = mEC$$,得 $$E$$ 坐标为 $$\left(\frac{m}{1+m}, \frac{\sqrt{3}m}{1+m}, \frac{3}{1+m}\right)$$。
平面 $$EAD$$ 的法向量为 $$\vec{n_1} = \vec{AD} \times \vec{AE}$$,平面 $$ADC$$ 的法向量为 $$\vec{n_2} = \vec{AD} \times \vec{AC}$$。
计算两平面夹角的正切值为 $$\frac{3}{2}$$,解得 $$m = 1$$,故选 B。
2. 解析:
法向量 $$\boldsymbol{m} = (1,2,-1)$$,$$\boldsymbol{n} = (1,-1,0)$$。
夹角余弦为 $$\cos \theta = \frac{\boldsymbol{m} \cdot \boldsymbol{n}}{|\boldsymbol{m}| |\boldsymbol{n}|} = \frac{1 \times 1 + 2 \times (-1) + (-1) \times 0}{\sqrt{6} \times \sqrt{2}} = \frac{-1}{2\sqrt{3}} = -\frac{\sqrt{3}}{6}$$。
由于夹角范围为 $$[0,90^\circ]$$,取正值 $$\frac{\sqrt{3}}{6}$$,故选 D。
3. 解析:
法向量 $$\boldsymbol{m} = (0,1,0)$$,$$\boldsymbol{n} = (0,1,1)$$。
夹角余弦为 $$\cos \theta = \frac{\boldsymbol{m} \cdot \boldsymbol{n}}{|\boldsymbol{m}| |\boldsymbol{n}|} = \frac{1}{\sqrt{2}} = \frac{\sqrt{2}}{2}$$,故夹角为 $$45^\circ$$,选 C。
4. 解析:
在正四面体中,通过坐标法或几何分析可得二面角的大小关系为 $$\gamma < \alpha < \beta$$,故选 D。
5. 解析:
同题3,两平面夹角为 $$45^\circ$$,选 A。
6. 解析:
随着 $$x$$ 增大,平面 $$BDE$$ 与平面 $$ABC$$ 的夹角先增大后减小,选 B。
7. 解析:
通过建立坐标系或几何法计算二面角的正弦值为 $$\frac{2\sqrt{5}}{5}$$,选 C。
8. 解析:
建立坐标系,计算两平面法向量的夹角余弦为 $$\frac{\sqrt{10}}{5}$$,选 D。
9. 解析:
同题4,二面角关系为 $$\gamma < \alpha < \beta$$,选 A。
10. 解析:
利用空间向量法,设二面角为 $$\theta$$,由 $$CD^2 = CA^2 + AB^2 + BD^2 - 2CA \cdot BD \cos \theta$$,解得 $$\theta = 60^\circ$$,选 C。
.jpg)