正确率60.0%已知$${{a}}$$为平面$${{α}}$$的法向量$${,{A}{,}{B}}$$是直线$${{b}}$$上的两点,则“$$a \cdot\overrightarrow{A B}=0$$”是“直线$${{b}{/}{/}}$$平面$${{α}}$$”的()
A
A.必要不充分条件
B.充分不必要条件
C.充要条件
D.既不充分也不必要条件
2、['平面与平面垂直的性质定理', '用空间向量研究空间中直线、平面的垂直', '用空间向量研究空间中直线、平面的平行', '平面的法向量及其应用']正确率40.0%在正方体$$A B C D-A_{1} B_{1} C_{1} D_{1}$$中,$${{E}}$$,$${{F}}$$分别为$$A B, B C$$的中点,则()
A
A.平面$$B_{1} E F \perp$$平面$${{B}{D}{{D}_{1}}}$$
B.平面$$B_{1} E F \perp$$平面$${{A}_{1}{B}{D}}$$
C.平面$$B_{1} E F / /$$平面$${{A}_{1}{A}{C}}$$
D.平面$$B_{1} E F / /$$平面$${{A}_{1}{{C}_{1}}{D}}$$
3、['用空间向量研究空间中直线、平面的垂直', '空间中直线的方向向量与直线的向量表示', '用空间向量研究空间中直线、平面的平行', '平面的法向量及其应用']正确率60.0%设两不同直线$${{a}{,}{b}}$$的方向向量分别是$$\vec{e_{1}}, ~ \vec{e_{2}},$$平面$${{α}}$$的法向量是$${{n}^{→}{,}}$$则下列推理;
其中正确的命题序号是()
B
A.$${①{②}{③}}$$
B.$${②{③}{④}}$$
C.$${①{③}{④}}$$
D.$${①{②}{④}}$$
4、['空间直角坐标系', '空间向量运算的坐标表示', '用空间向量研究平面与平面之间的距离', '用空间向量研究点到平面的距离', '平面的法向量及其应用']正确率40.0%若正方体$$A B C D-A_{1} B_{1} C_{1} D_{1}$$的棱长为$${{1}{,}}$$则平面$${{A}_{1}{B}{D}}$$与平面$${{B}_{1}{C}{{D}_{1}}}$$间的距离为()
B
A.$$\frac{\sqrt3} {2}$$
B.$$\frac{\sqrt{3}} {3}$$
C.$$\frac{2 \sqrt{2}} {3}$$
D.$$\frac{2 \sqrt{3}} {3}$$
5、['空间直角坐标系', '用空间向量研究点到平面的距离', '平面的法向量及其应用']正确率40.0%如图所示,在长方体$$A B C D-A_{1} B_{1} C_{1} D_{1}$$中$${,}$$$$A D=A A_{1}=2, \, \, \, A B=4,$$点$${{E}}$$是棱$${{A}{B}}$$的中点,则点$${{E}}$$到平面$${{A}{C}{{D}_{1}}}$$的距离为()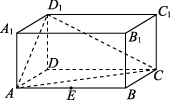
B
A.$${{1}}$$
B.$$\begin{array} {l l} {\frac{2} {3}} \\ \end{array}$$
C.$$\frac{1} {3}$$
D.$${\sqrt {2}}$$
6、['平面的法向量及其应用', '用空间向量研究空间中直线、平面的平行']正确率60.0%若平面$${{α}}$$的一个法向量是$$\boldsymbol{n}=\left( \frac{1} {2},-1, \frac{1} {3} \right)$$,平面$${{β}}$$的一个法向量是$$\boldsymbol{m}=(-3, 6,-2 )$$,则平面$${{α}}$$与平面$${{β}}$$的位置关系是()
C
A.平行
B.重合
C.平行或重合
D.垂直
7、['空间向量的坐标与空间向量的平行、垂直', '用空间向量研究空间中直线、平面的垂直', '空间中直线的方向向量与直线的向量表示', '平面的法向量及其应用']正确率60.0%设直线$${{l}}$$的方向向量为$$\overrightarrow{u}=(-2, 2, t )$$,平面$${{α}}$$的法向量为$$\overrightarrow{v}=( 6,-6, 1 2 )$$,若直线$${{l}{⊥}}$$平面$${{α}}$$,则实数$${{t}}$$等于()
B
A.$${{4}}$$
B.$${{−}{4}}$$
C.$${{2}}$$
D.$${{−}{2}}$$
8、['充分、必要条件的判定', '空间中直线的方向向量与直线的向量表示', '平面的法向量及其应用', '直线与平面所成的角']正确率60.0%设平面$${{α}}$$的法向量为$${{n}^{→}}$$,直线$${{l}}$$的方向向量为$${{m}^{→}}$$,那么$$\4 < \overrightarrow{m}, ~ \overrightarrow{n} >=6 0^{\circ n}$$是$${{“}}$$直线$${{l}}$$与平面$${{α}}$$夹角为$${{3}{0}^{∘}{”}}$$的()
A
A.充分而不必要条件
B.必要而不充分条件
C.充分必要条件
D.既不充分也不必要条件
9、['平面的法向量及其应用']正确率80.0%设平面$${{α}}$$的法向量为$$( 1,-2, \lambda)$$,平面$${{β}}$$的法向量为$$( 2, \mu, 4 )$$,若$${{α}{/}{/}{β}}$$,则$$\lambda+\mu=( \begin{array} {c} {} \\ {} \\ \end{array} )$$
C
A.$${{2}}$$
B.$${{4}}$$
C.$${{−}{2}}$$
D.$${{−}{4}}$$
10、['用空间向量研究距离、夹角问题', '平面的法向量及其应用']正确率80.0%设直线$${{l}}$$的一个方向向量为$${{v}^{→}}$$,平面$${{α}}$$的一个法向量为$${{n}^{→}}$$,平面$${{β}}$$的一个法向量为$${{m}^{→}}$$,则下列说法正确的是$${{(}{)}}$$
①若$$\overrightarrow{v}, \overrightarrow{n}=3 0^{\circ}$$,则$${{l}}$$与$${{α}}$$所成的角为$${{3}{0}{°}}$$;
②若$${{l}}$$与$${{α}}$$所成角为$${{6}{0}{°}}$$,则$$\overrightarrow{v}, \overrightarrow{n}=3 0^{\circ}$$;
③若$$\overrightarrow{m}, \overrightarrow{n}=6 0^{\, \circ}$$,则平面$${{α}}$$与$${{β}}$$所成的锐二面角为$${{6}{0}{°}}$$;
④若平面$${{α}}$$与$${{β}}$$所成的角为$${{6}{0}{°}}$$,则$$\overrightarrow{m}, \overrightarrow{n}=6 0^{\, \circ}$$
A.③
B.①③
C.②④
D.①③④
1. 解析:
2. 解析:
3. 解析:
4. 解析:
5. 解析:
6. 解析:
7. 解析:
8. 解析:
9. 解析:
10. 解析:
.jpg)