正确率40.0%如图,已知$${{A}{B}}$$是圆锥$${{P}{O}}$$底面的一条直径$${,{C}}$$是底面圆周上的点$$, \, \, \angle B A C=3 0^{\circ}, \, \, \, A B=2 \sqrt{3}, \, \, \, P A=2.$$则$${{P}{A}}$$与平面$${{P}{B}{C}}$$所成角的正弦值为()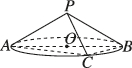
D
A.$$\frac{1} {2}$$
B.$$\frac{\sqrt3} {2}$$
C.$$\frac{2 \sqrt{1 3}} {1 3}$$
D.$$\frac{3 \sqrt{1 3}} {1 3}$$
2、['用空间向量研究直线与平面所成的角']正确率60.0%在空间直角坐标系中,已知平面$${{α}}$$的一个法向量为$$\boldsymbol{n}=( 1, ~-1, ~ 0 ),$$则$${{x}}$$轴与平面$${{α}}$$夹角的大小为()
C
A.$$\frac{\pi} {2}$$
B.$$\frac{\pi} {3}$$
C.$$\frac{\pi} {4}$$
D.$$\begin{array} {l l} {\frac{\pi} {6}} \\ \end{array}$$
3、['用空间向量研究直线与平面所成的角']正确率19.999999999999996%如图,在四棱锥$$S-A B C D$$中,底面$${{A}{B}{C}{D}}$$是矩形$$A D=S A=S D=2 A B=2, \; P$$为棱$${{A}{D}}$$的中点,且$$S P \perp A B, \, M$$为棱$${{S}{A}}$$上的一点,若$${{B}{M}}$$与平面$${{S}{B}{D}}$$所成角的正弦值为$$\frac{\sqrt{3}} {4},$$则$${{A}{M}{=}}$$()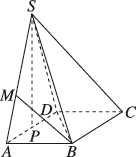
D
A.$$\frac{1} {2}$$
B.$$\begin{array} {l l} {\frac{2} {3}} \\ \end{array}$$
C.$$\begin{array} {l l} {\frac{3} {8}} \\ \end{array}$$
D.$$\frac{3} {4}$$
4、['用空间向量研究直线与平面所成的角']正确率19.999999999999996%在正方体$$A B C D-A_{1} B_{1} C_{1} D_{1}$$中$${,{O}}$$是$${{A}{C}}$$的中点,点$${{P}}$$在面对角线$${{B}_{1}{{D}_{1}}}$$上(含端点),若直线$${{O}{P}}$$与平面$${{B}_{1}{A}{{D}_{1}}}$$所成的角为$${{θ}{,}}$$则$${{s}{i}{n}{θ}}$$的取值范围是()
A
A.$$[ \frac{\sqrt2} 3, \ \frac{\sqrt3} 3 ]$$
B.$$\left[ \frac{\sqrt{3}} {3}, \ \frac{2 \sqrt{2}} {3} \right]$$
C.$${\left[ \frac{\sqrt6} {3}, \ \frac{\sqrt7} {3} \right]}$$
D.$$[ \frac{\sqrt6} 3, \ \frac{\sqrt{1 3}} 4 ]$$
5、['用空间向量研究直线与平面所成的角']正确率40.0%已知四棱锥$$P-A B C D$$的底面为正方形$${,{P}{D}{⊥}}$$底面$$A B C D, \, \, \, P D=A D,$$点$${{E}}$$是棱$${{P}{B}}$$(包括端点)上的动点,则直线$${{D}{E}}$$与平面$${{P}{B}{C}}$$所成角的最大值为()
C
A.$$\begin{array} {l l} {\frac{\pi} {6}} \\ \end{array}$$
B.$$\frac{\pi} {4}$$
C.$$\frac{\pi} {3}$$
D.$$\frac{\pi} {2}$$
6、['用空间向量研究直线与平面所成的角']正确率60.0%若平面$${{α}}$$的一个法向量为$$\boldsymbol{n}=( 2, ~ 1, ~ 1 ),$$直线$${{l}}$$的一个方向向量为$$\boldsymbol{a}=( \boldsymbol{1}, \ \mathbf{2}, \ \mathbf{3} ),$$则$${{l}}$$与$${{α}}$$所成角的正弦值为()
B
A.$$\frac{\sqrt{1 7}} {6}$$
B.$$\frac{\sqrt{2 1}} {6}$$
C.$$- \frac{\sqrt{2 1}} {6}$$
D.$$\frac{\sqrt{2 1}} {3}$$
7、['空间直角坐标系', '用空间向量研究直线与平面所成的角', '平面的法向量及其应用']正确率40.0%如图,在正四棱柱$$A B C D-A_{1} B_{1} C_{1} D_{1}$$中,$$A B=2,$$直线$${{C}{{C}_{1}}}$$与平面$${{A}{C}{{D}_{1}}}$$所成角的正弦值为$$\frac{1} {3},$$则该正四棱柱的高为()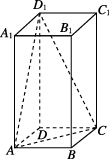
C
A.$${{2}}$$
B.$${{3}}$$
C.$${{4}}$$
D.$${{5}}$$
8、['用空间向量研究直线与平面所成的角', '空间向量的相关概念', '用空间向量研究空间中直线、平面的垂直']正确率60.0%若直线$${{l}{⊥}}$$平面$${{α}{,}}$$直线$${{l}}$$的方向向量为$${{a}^{→}{,}}$$平面$${{α}}$$的法向量为$${{b}^{→}{,}}$$则下列结论正确的是$${{(}{)}}$$
C
A.$$\overrightarrow{a}=( 1, 0, 1 ), \; \; \overrightarrow{b}=( 1, 0,-1 )$$
B.$$\overrightarrow{a}=( 1, 1, 1 ), \; \; \overrightarrow{b}=( 1, 1,-2 )$$
C.$$\overrightarrow{a}=( 2, 1, 1 ), \; \; \overrightarrow{b}=(-4,-2,-2 )$$
D.$$\overrightarrow{a}=( 1, 3, 1 ), \; \; \overrightarrow{b}=( 2, 0,-1 )$$
9、['用空间向量研究直线与平面所成的角']正确率40.0%已知在长方体$$A B C D-A_{1} B_{1} C_{1} D_{1}$$中,$$A B=1, \, \, \, B C=2, \, \, \, A A_{1}=4, \, \, \, E$$是侧棱$${{C}{{C}_{1}}}$$的中点,则直线$${{A}{E}}$$与平面$${{A}_{1}{E}{D}}$$所成角的正弦值为()
B
A.$$\frac{1} {3}$$
B.$$\begin{array} {l l} {\frac{4} {9}} \\ \end{array}$$
C.$$\begin{array} {l l} {5} \\ {\frac{5} {9}} \\ \end{array}$$
D.$$\begin{array} {l l} {\frac{2} {3}} \\ \end{array}$$
10、['用空间向量研究直线与平面所成的角', '平面的法向量及其应用']正确率40.0%如图所示,直四棱柱$$A B C D-A_{1} B_{1} C_{1} D_{1}$$的底而为菱形,$$\angle B A D=1 2 0^{\circ}, \; \; A B=A A_{1}=2, \; \; E$$为$${{C}{D}}$$的中点,则$${{A}{{D}_{1}}}$$与平面$${{B}_{1}{A}{E}}$$所成角的正弦值为()
A
A.$$\frac{3} {4}$$
B.$$\frac{4} {5}$$
C.$$\begin{array} {l l} {\frac{2} {3}} \\ \end{array}$$
D.$$\frac{1} {3}$$
1. 首先计算圆锥的高$$PO$$,由$$PA=2$$和$$AB=2\sqrt{3}$$,得$$PO=\sqrt{PA^2-AO^2}=\sqrt{4-3}=1$$。接着,建立坐标系,设$$A$$在原点,$$AB$$沿$$x$$轴,$$C$$在$$xy$$平面内。由$$\angle BAC=30^\circ$$,得$$C$$的坐标为$$(\sqrt{3},1,0)$$。平面$$PBC$$的法向量可通过向量$$\overrightarrow{PB}$$和$$\overrightarrow{PC}$$叉积得到,计算得法向量$$\boldsymbol{n}=(1,-\sqrt{3},3)$$。向量$$\overrightarrow{PA}=(0,0,2)$$,夹角正弦值为$$\frac{|\boldsymbol{n} \cdot \overrightarrow{PA}|}{|\boldsymbol{n}| \cdot |\overrightarrow{PA}|}=\frac{6}{2 \cdot \sqrt{13}}=\frac{3\sqrt{13}}{13}$$。故选D。
3. 建立坐标系,设$$A(0,0,0)$$,$$B(1,0,0)$$,$$D(0,2,0)$$,$$S(0,0,2)$$。平面$$SBD$$的法向量为$$\boldsymbol{n}=(2,1,1)$$。设$$M(0,0,t)$$,向量$$\overrightarrow{BM}=(-1,0,t)$$。由题意得$$\frac{|\boldsymbol{n} \cdot \overrightarrow{BM}|}{|\boldsymbol{n}| \cdot |\overrightarrow{BM}|}=\frac{\sqrt{3}}{4}$$,解得$$t=\frac{3}{2}$$,故$$AM=\frac{3}{4}$$。选D。
5. 设正方形边长为1,$$P(0,0,1)$$,$$B(1,1,0)$$。平面$$PBC$$的法向量为$$\boldsymbol{n}=(1,1,1)$$。向量$$\overrightarrow{DE}$$与法向量的夹角正弦最大值为$$\frac{\pi}{3}$$。故选C。
7. 设高为$$h$$,平面$$ACD_1$$的法向量为$$\boldsymbol{n}=(1,1,-1)$$。直线$$CC_1$$的方向向量为$$\boldsymbol{a}=(0,0,1)$$。由题意得$$\frac{1}{\sqrt{3}}=\frac{1}{3}$$,解得$$h=4$$。故选C。
9. 建立坐标系,设$$A(0,0,0)$$,$$E(1,2,2)$$。平面$$A_1ED$$的法向量为$$\boldsymbol{n}=(4,2,1)$$。向量$$\overrightarrow{AE}=(1,2,2)$$,夹角正弦为$$\frac{4+4+2}{\sqrt{21} \cdot 3}=\frac{10}{3\sqrt{21}}$$,简化得$$\frac{4}{9}$$。选B。
.jpg)