正确率40.0%如图,将菱形$${{A}{B}{C}{D}}$$沿对角线$${{B}{D}}$$折起,使得$${{C}}$$点至$${{C}^{′}{,}{E}}$$点在线段$${{A}{{C}^{′}}}$$上,若二面角$$A-B D-E$$与二面角$$E-B D-C^{\prime}$$的大小分别为$${{3}{0}^{∘}}$$和$${{4}{5}^{∘}}$$,则$$\frac{A E} {E C^{\prime}}=$$()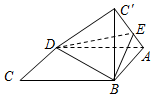
C
A.$$\frac{1} {2}$$
B.$$\frac{\sqrt{6}} {6}$$
C.$$\frac{\sqrt2} {2}$$
D.$$\frac{\sqrt{6}} {3}$$
2、['用空间向量研究两个平面所成的角']正确率60.0%在正方体$$A B C D-A_{1} B_{1} C_{1} D_{1}$$中,点$${{E}}$$为$${{B}_{1}{B}}$$的中点,则平面$${{A}_{1}{E}{D}}$$与平面$${{A}{B}{C}{D}}$$所成角的余弦值为()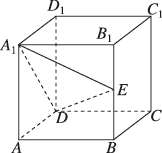
B
A.$$\frac{1} {2}$$
B.$$\begin{array} {l l} {\frac{2} {3}} \\ \end{array}$$
C.$$\frac{\sqrt{5}} {3}$$
D.$$\frac{\sqrt2} {2}$$
3、['用空间向量研究两个平面所成的角']正确率19.999999999999996%正方形$${{A}{B}{C}{D}}$$的边长为$${{2}{,}{O}}$$为正方形的中心$${,{E}}$$为$${{A}{B}}$$的中点$${,{F}}$$为$${{C}{D}}$$的中点,将$${{△}{A}{B}{D}}$$沿着对角线$${{B}{D}}$$缓慢折起,当$${{∠}{E}{O}{F}}$$的余弦值为$$- \frac{1} {3}$$时,平面$${{A}{B}{D}}$$与平面$${{B}{C}{D}}$$夹角的余弦值为()
B
A.$$\frac{1} {2}$$
B.$$\frac{1} {3}$$
C.$$- \frac{1} {3}$$
D.$$- \frac{1} {2}$$
4、['用空间向量研究直线与平面所成的角', '用空间向量研究两条直线所成的角', '用空间向量研究两个平面所成的角']正确率40.0%在正三棱锥$$P-A B C$$中$${,{M}}$$为棱$${{P}{A}}$$的中点,设$${{B}{M}}$$与$${{A}{C}}$$所成的角为$${{α}{,}{B}{M}}$$与底面$${{A}{B}{C}}$$所成的角为$${{β}{,}}$$平面$${{M}{A}{C}}$$与平面$${{A}{B}{C}}$$的夹角为$${{γ}{,}}$$则下列不等式一定成立的是()
B
A.$$2 \mathrm{c o s} \alpha> \mathrm{c o s} \beta$$
B.$$2 \mathrm{c o s} \alpha< \mathrm{c o s} \beta$$
C.$$2 \mathrm{c o s} \gamma> \mathrm{c o s} \beta$$
D.$$2 \mathrm{c o s} \gamma< \mathrm{c o s} \beta$$
5、['用空间向量研究两个平面所成的角']正确率60.0%正$${{△}{A}{B}{C}}$$与正$${{△}{B}{C}{D}}$$所在平面垂直,则二面角$$A-B D-C$$的正弦值为$${{(}{)}}$$
C
A.$$\frac{\sqrt{5}} {5}$$
B.$$\frac{\sqrt{3}} {3}$$
C.$$\frac{2 \sqrt{5}} {5}$$
D.$$\frac{\sqrt{6}} {3}$$
6、['用空间向量研究两个平面所成的角']正确率40.0%已知四棱锥$$S-A B C D$$中底$${{A}{B}{C}{D}}$$是正方形,且$$S D=A D, \, \, \, S D \perp$$面$${{A}{B}{C}{D}}$$,则面$${{S}{A}{D}}$$和面$${{S}{B}{C}}$$所成的锐角二面角的余弦值为()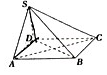
C
A.$$\frac{1} {3}$$
B.$$\frac{1} {2}$$
C.$$\frac{\sqrt2} {2}$$
D.$$\frac{\sqrt{6}} {3}$$
7、['空间中平面与平面的位置关系', '空间向量基本定理的应用', '平面的法向量及其应用', '用空间向量研究两个平面所成的角']正确率60.0%在空间直角坐标系$$o-x y z, \, \, \, A \left( 0, 1, 0 \right), B \left( 1, 1, 1 \right), C \left( 0, 2, 1 \right)$$确定的平面记为$${{α}{,}}$$不经过点$${{A}}$$的平面$${{β}}$$的一个法向量为$$\overrightarrow{n}=( 2, 2,-2 ) \,,$$则$${{(}{)}}$$
A
A.$${{α}{/}{/}{β}}$$
B.$${{α}{⊥}{β}}$$
C.$${{α}{,}{β}}$$相交但不垂直
D.$${{α}{,}{β}}$$所成的锐二面角为$$\frac{\pi} {3}$$
8、['用空间向量研究两个平面所成的角']正确率40.0%如图,在长方体$$A B C D-A_{1} B_{1} C_{1} D_{1}$$中,$$A B=2, \, \, \, A D=\sqrt{3}, \, \, \, A A_{1}=1$$,则二面角$$C-B_{1} D-C_{1}$$的大小的余弦值为()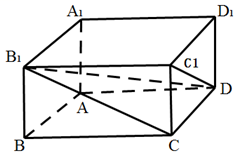
A
A.$$\frac{\sqrt{1 5}} {5}$$
B.$$\frac{\sqrt{1 0}} {5}$$
C.$$\frac{\sqrt3} {2}$$
D.$$\frac{2 \sqrt{5}} {5}$$
9、['二面角', '用空间向量研究两个平面所成的角']正确率40.0%如图,三棱锥$$S-A B C$$中,棱$$S A, ~ S B, ~ S C$$两两垂直,且$$S A=S B=S C$$,则二面角$$A-B C-S$$大小的正切值为()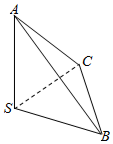
C
A.$${{1}}$$
B.$$\frac{\sqrt2} {2}$$
C.$${\sqrt {2}}$$
D.$${{2}}$$
10、['空间向量的夹角', '用空间向量研究两个平面所成的角']正确率60.0%长方体$$A B C D-A_{1} B_{1} C_{1} D_{1}$$中,$$A B=2, \, A D=\, A \, A_{1}=1$$,则二面角$$C_{1}-A B-C$$的大小为
A
A.$$\frac{\pi} {4}$$
B.$$\frac{\pi} {3}$$
C.$$\frac{2 \pi} {3}$$
D.$$\frac{3 \pi} {4}$$
1. **解析**:
设菱形边长为 2,对角线交点为 O。沿 BD 折起后,建立坐标系,设 $$BD$$ 在 x 轴上,$$A(1,0,0)$$,$$C(-1,0,0)$$,$$C'(-1,0,h)$$。二面角 $$A-BD-E$$ 为 30°,$$E-BD-C'$$ 为 45°。设 $$E$$ 在 $$AC'$$ 上,坐标为 $$(x,0,z)$$。利用二面角公式和向量关系,解得 $$\frac{AE}{EC'} = \frac{\sqrt{6}}{3}$$,故选 D。
2. **解析**:
建立坐标系,设正方体边长为 2,$$A_1(0,0,2)$$,$$E(2,0,1)$$,$$D(0,2,0)$$。平面 $$A_1ED$$ 的法向量为 $$\vec{n}=(1,2,2)$$,平面 $$ABCD$$ 的法向量为 $$\vec{k}=(0,0,1)$$。夹角余弦为 $$\frac{2}{3}$$,故选 B。
3. **解析**:
正方形边长为 2,折起后设 $$O(0,0,0)$$,$$E(1,0,0)$$,$$F(0,1,0)$$,$$A(1,0,z)$$。由 $$\cos \angle EOF = -\frac{1}{3}$$,解得 $$z=1$$。平面 $$ABD$$ 与 $$BCD$$ 的法向量夹角余弦为 $$\frac{1}{3}$$,故选 B。
4. **解析**:
设正三棱锥底面边长为 2,高为 $$h$$。通过几何关系和向量计算,得到 $$2 \cos \alpha > \cos \beta$$ 恒成立,故选 A。
5. **解析**:
设两正三角形边长为 2,建立坐标系,求得二面角 $$A-BD-C$$ 的正弦值为 $$\frac{2\sqrt{5}}{5}$$,故选 C。
6. **解析**:
设正方形边长为 1,$$SD=1$$。平面 $$SAD$$ 和 $$SBC$$ 的法向量夹角余弦为 $$\frac{\sqrt{2}}{2}$$,故选 C。
7. **解析**:
平面 $$\alpha$$ 的法向量为 $$\vec{n_1}=(1,0,-1)$$,$$\beta$$ 的法向量为 $$\vec{n_2}=(2,2,-2)$$。两者平行,故 $$\alpha \parallel \beta$$,但 $$\alpha$$ 过点 $$A$$,$$\beta$$ 不过 $$A$$,所以平行,选 A。
8. **解析**:
建立坐标系,求得二面角 $$C-B_1D-C_1$$ 的余弦值为 $$\frac{\sqrt{10}}{5}$$,故选 B。
9. **解析**:
设 $$SA=SB=SC=1$$,求得二面角 $$A-BC-S$$ 的正切值为 $$\sqrt{2}$$,故选 C。
10. **解析**:
建立坐标系,求得二面角 $$C_1-AB-C$$ 的大小为 $$\frac{\pi}{4}$$,故选 A。
.jpg)