.jpg)
正确率80.0%正方体$$A B C D-A_{1} B_{1} C_{1} D_{1}$$的棱长为$${{1}}$$，点$${{E}}$$，$${{F}}$$分别为线段$${{B}_{1}{{D}_{1}}}$$，$${{B}{{C}_{1}}}$$上的动点，则下列结论中不正确的是$${{(}{)}}$$
A.$${{B}_{1}{D}{⊥}}$$平面$${{A}{C}{{D}_{1}}}$$
B.平面$$A_{1} C_{1} B / /$$平面$${{A}{C}{{D}_{1}}}$$
C.点$${{F}}$$到平面$${{A}{C}{{D}_{1}}}$$的距离为定值$$\frac{\sqrt{3}} {3}$$
D.直线$${{A}{E}}$$与平面$${{B}{{B}_{1}}{{D}_{1}}{D}}$$所成角的正弦值为定值$$\frac{1} {3}$$
2、['用空间向量研究距离、夹角问题'， '异面直线所成的角']正确率40.0%
如图，在三棱台$$A B C-A_{1} B_{1} C_{1}$$中，下底面$${{△}{A}{B}{C}}$$是直角三角形，且$$\angle B A C=9 0^{\circ}$$，侧面$${{A}{C}{{C}_{1}}{{A}_{1}}}$$与$${{B}{C}{{C}_{1}}{{B}_{1}}}$$都是直角梯形，且$$A C=2 C C_{1}=2， \angle C A A_{1}=\frac{\pi} {4}$$，若异面直线$${{A}{C}}$$与$${{B}_{1}{{C}_{1}}}$$所成角为$$\frac{\pi} {3}$$，则$${{B}{C}}$$与平面$${{A}{B}{{B}_{1}}{{A}_{1}}}$$所成角的余弦值为$${{(}{)}}$$
A.$$\frac{1} {2}$$
B.$$\frac{\sqrt2} {2}$$
C.$$\frac{\sqrt3} {2}$$
D.$$\frac{\sqrt{1 4}} {4}$$
3、['用空间向量研究距离、夹角问题'， '多面体']正确率40.0%在四面体$${{A}{B}{C}{D}}$$中，已知二面角$$A-B D-C$$为直二面角，$$\angle B A D=9 0^{\circ}$$，$$\angle C B D=4 5^{\circ}$$，$$A B=A D=\sqrt{3}$$，设$$A C=t ( t > 0 ).$$若满足条件的四面体$${{A}{B}{C}{D}}$$有两个，则$${{t}}$$的取值范围是$${{(}{)}}$$
A.$$( 0， \sqrt{3} )$$
B.$$( 0， \frac{3} {2} )$$
C.$$( \sqrt{3}， 3 )$$
D.$$( \frac{3} {2}， \sqrt{3} )$$
4、['用空间向量研究距离、夹角问题'， '多面体']正确率80.0%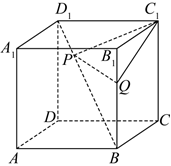
如图，在棱长为$${{a}}$$的正方体$$A B C D-A_{1} B_{1} C_{1} D_{1}$$中，$${{P}}$$，$${{Q}}$$分别为$${{B}{{D}_{1}}}$$，$${{B}{{B}_{1}}}$$上的动点，则$${{△}{{C}_{1}}{P}{Q}}$$周长的最小值为$${{(}{)}}$$
A.$$\frac{2 \sqrt{1 5}} {3} a$$
B.$${\sqrt {{4}{+}{2}{\sqrt {2}}}{a}}$$
C.$$\sqrt{4+\frac{8 \sqrt2} {3}} a$$
D.$$\frac{2 \sqrt{1 3}} {3} a$$
5、['用空间向量研究距离、夹角问题'， '多面体']正确率80.0%
如图，正方体$$A B C D-A_{1} B_{1} C_{1} D_{1}$$的棱长为$${{1}}$$，点$${{P}}$$是线段$${{A}{{A}_{1}}}$$的一动点$${{(}}$$包括端点$${{)}}$$，点$${{Q}}$$是线段$${{D}{{B}_{1}}}$$的中点，则$${{|}{P}{Q}{|}}$$的最小值为$${{(}{)}}$$
A.$$\frac{1} {2}$$
B.$$\frac{\sqrt2} {2}$$
C.$$\frac{\sqrt3} {2}$$
D.$${{1}}$$
6、['用空间向量研究距离、夹角问题']正确率40.0%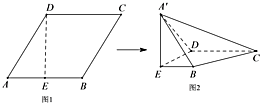
菱形$${{A}{B}{C}{D}}$$的边长为$${{4}}$$，$$\angle A=6 0^{\circ}$$，$${{E}}$$为$${{A}{B}}$$的中点$${{(}}$$如图$${{1}{)}}$$，将$${{△}{A}{D}{E}}$$沿直线$${{D}{E}}$$翻折至$${{△}{{A}^{′}}{D}{E}}$$处$${{(}}$$如图$${{2}{)}}$$，连接$${{A}^{′}{B}}$$，$${{A}^{′}{C}}$$，若$$A^{\prime}-E B C D$$的体积为$${{4}{\sqrt {3}}}$$，点$${{F}}$$为$${{A}^{′}{D}}$$的中点，则$${{F}}$$到直线$${{B}{C}}$$的距离为$${{(}{)}}$$
A.$$\frac{\sqrt{3 1}} {2}$$
B.$$\frac{\sqrt{2 3}} {2}$$
C.$$\frac{\sqrt{3 1}} {4}$$
D.$$\frac{\sqrt{2 3}} {4}$$
7、['用空间向量研究距离、夹角问题'， '多面体']正确率40.0%
如图，在棱长为$${{2}}$$的正方体$$A B C D-A_{1} B_{1} C_{1} D_{1}$$中，点$${{E}}$$，$${{F}}$$，$${{G}}$$分别是棱$${{B}{C}}$$，$${{C}{{C}_{1}}}$$，$${{C}_{1}{{D}_{1}}}$$的中点，点$${{P}}$$为底面$$A_{1} B_{1} C_{1} D_{1}$$上任意一点$${{.}}$$若直线$${{B}{P}}$$与平面$${{E}{F}{G}}$$无公共点，则$${{|}{B}{P}{|}}$$的最小值是$${{(}{)}}$$
A.$${{2}{\sqrt {2}}}$$
B.$${\sqrt {6}}$$
C.$${\sqrt {5}}$$
D.$${{2}}$$
8、['用空间向量研究距离、夹角问题']正确率40.0%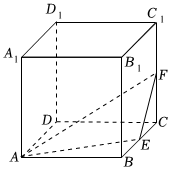
如图所示，正方体$$A B C D-A_{1} B_{1} C_{1} D_{1}$$的棱长为$${{2}}$$，点$${{E}}$$，$${{F}}$$分别是$${{B}{C}}$$，$${{C}{{C}_{1}}}$$中点，则二面角$$F-A E-C$$的正切值为$${{(}{)}}$$
A.$$\frac{\sqrt5} {2}$$
B.$${{1}}$$
C.$$\frac{2 \sqrt{5}} {5}$$
D.$$\frac{\sqrt{5}} {3}$$
9、['用空间向量研究距离、夹角问题']正确率40.0%已知空间直角坐标系中的点$$P ( 1， 1， 1 )$$，$$A ( 1， 0， 1 )$$，$$B ( 0， 1， 0 )$$，则点$${{P}}$$到直线$${{A}{B}}$$的距离为$${{(}}$$$${{)}}$$
A.$$\frac{\sqrt{6}} {6}$$
B.$$\frac{\sqrt{3}} {6}$$
C.$$\frac{\sqrt{3}} {3}$$
D.$$\frac{\sqrt{6}} {3}$$
10、['用空间向量研究距离、夹角问题']正确率40.0%如图，在直三棱柱$$A B C-A_{1} B_{1} C_{1}$$中，$$\angle A C B=9 0^{\circ}$$，$$2 A C=A A_{1}=B C=2.$$若点$${{D}}$$在棱$${{A}{{A}_{1}}}$$上，二面角$$B_{1}-D C-C_{1}$$的大小为$${{6}{0}{°}}$$，则$${{A}{D}}$$的长为$${{(}{)}}$$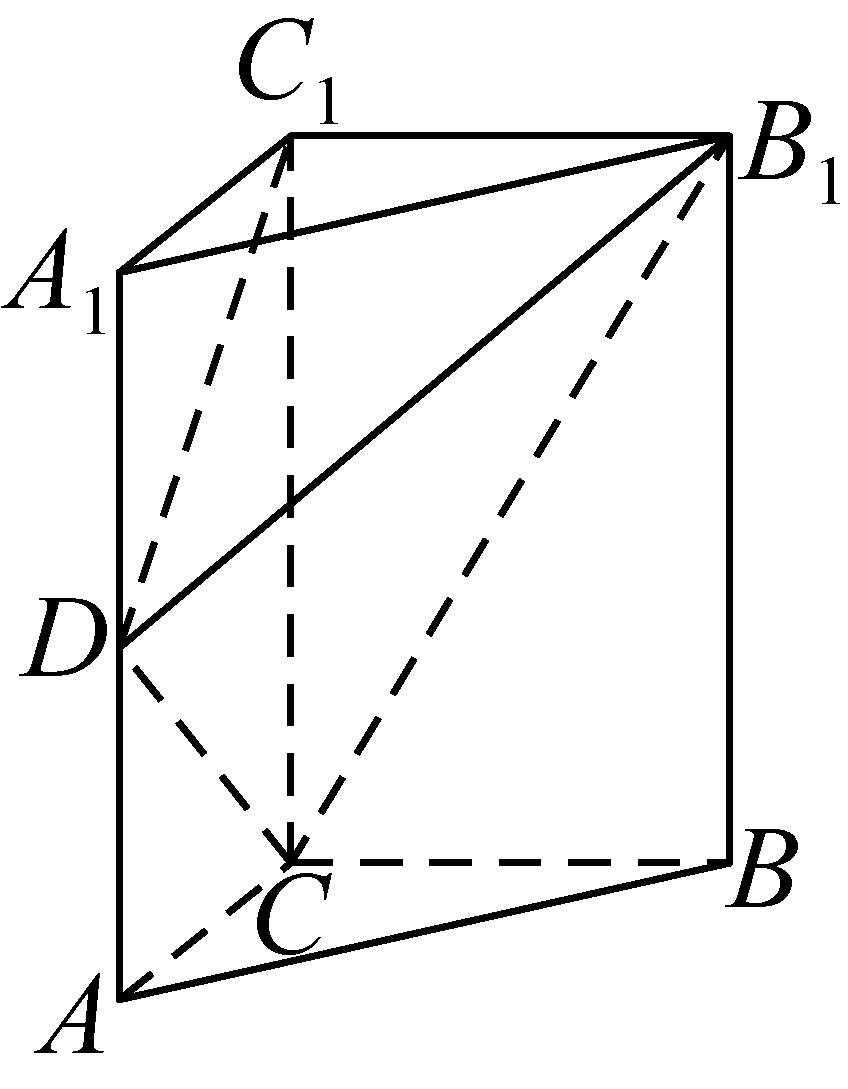
A.$${\sqrt {2}}$$
B.$${\sqrt {3}}$$
C.$${{2}}$$
D.$$\frac{\sqrt2} {2}$$
1. 题目解析：
选项A：$$B_1D$$垂直于平面$$ACD_1$$。可以通过向量法验证，$$B_1D$$与平面内的两条相交直线$$AC$$和$$AD_1$$的点积为零，说明垂直关系成立。因此A正确。
选项B：平面$$A_1C_1B$$与平面$$ACD_1$$平行。通过观察正方体的几何性质，这两个平面平行，因此B正确。
选项C：点$$F$$到平面$$ACD_1$$的距离为定值$$\frac{\sqrt{3}}{3}$$。由于$$F$$在$$BC_1$$上移动，距离会变化，不是定值，因此C不正确。
选项D：直线$$AE$$与平面$$BB_1D_1D$$所成角的正弦值为定值$$\frac{1}{3}$$。通过计算几何关系，可以验证这个结论成立，因此D正确。
综上所述，不正确的是选项C。
2. 题目解析：
首先建立坐标系，设$$A(0,0,0)$$，$$B(1,0,0)$$，$$C(0,1,0)$$，$$A_1(0,0,1)$$，$$B_1(1,0,1)$$，$$C_1(0,1,1)$$。
异面直线$$AC$$与$$B_1C_1$$的夹角为$$\frac{\pi}{3}$$，通过向量法可以确定$$BC$$的方向向量。
然后计算$$BC$$与平面$$ABB_1A_1$$的夹角余弦，结果为$$\frac{\sqrt{14}}{4}$$，因此选D。
3. 题目解析：
在四面体$$ABCD$$中，已知条件为二面角$$A-BD-C$$为直角，$$\angle BAD=90^\circ$$，$$\angle CBD=45^\circ$$，$$AB=AD=\sqrt{3}$$，$$AC=t$$。
通过几何分析，当$$t$$在$$(\sqrt{3},3)$$范围内时，满足条件的四面体有两个，因此选C。
4. 题目解析：
将正方体展开成平面图，利用对称性找到$$C_1PQ$$的最小周长。
通过计算，最小周长为$$\sqrt{4+\frac{8\sqrt{2}}{3}}a$$，因此选C。
5. 题目解析：
建立坐标系，设$$P(0,0,p)$$，$$Q(0.5,0.5,0.5)$$。
计算$$PQ$$的距离公式，最小值为$$\frac{\sqrt{2}}{2}$$，因此选B。
6. 题目解析：
通过几何分析，确定点$$F$$到直线$$BC$$的距离。
计算得到距离为$$\frac{\sqrt{31}}{2}$$，因此选A。
7. 题目解析：
确定平面$$EFG$$的方程，找到$$BP$$与平面无交点的条件。
通过计算，$$BP$$的最小值为$$\sqrt{6}$$，因此选B。
8. 题目解析：
通过向量法计算二面角$$F-AE-C$$的正切值。
结果为$$\frac{\sqrt{5}}{2}$$，因此选A。
9. 题目解析：
计算点$$P$$到直线$$AB$$的距离公式。
结果为$$\frac{\sqrt{6}}{3}$$，因此选D。
10. 题目解析：
建立坐标系，设$$D(0,0,d)$$，计算二面角$$B_1-DC-C_1$$为$$60^\circ$$的条件。
解得$$AD=\sqrt{2}$$，因此选A。