.jpg)
正确率60.0%在正方体$$A B C D-A_{1} B_{1} C_{1} D_{1}$$中$${，{M}}$$是棱$${{C}_{1}{{D}_{1}}}$$(不含端点)上的动点$${，{N}}$$为$${{B}{C}}$$的中点，则（）
B
A.$$B D \perp A M$$
B.平面$$A_{1} B D \perp$$平面$${{A}{{D}_{1}}{M}}$$
C.$${{M}{N}{/}{/}}$$平面$${{A}_{1}{B}{D}}$$
D.$${{C}{M}{/}{/}}$$平面$${{A}_{1}{B}{D}}$$
2、['空间直角坐标系'， '用空间向量研究距离、夹角问题'， '空间向量的数量积'， '用空间向量研究空间中直线、平面的平行'， '空间向量的线性运算']正确率40.0%
如图，在棱长为$${{1}}$$的正方体$$A B C D-A_{1} B_{1} C_{1} D_{1}$$中，$${{P}}$$，$${{Q}}$$分别是线段$${{C}{{C}_{1}}}$$，$${{B}{D}}$$上的点，$${{R}}$$是直线$${{A}{D}}$$上的点，满足$${{P}{Q}{/}{/}}$$平面$${{A}{B}{{C}_{1}}{{D}_{1}}}$$，$$P Q \perp R Q$$，且$${{P}}$$、$${{Q}}$$不是正方体的顶点，则$${{|}{P}{R}{|}}$$的最小值是$${{(}{)}}$$
A.$$\frac{\sqrt{4 2}} {6}$$
B.$$\frac{\sqrt{3 0}} {5}$$
C.$$\frac{\sqrt5} {2}$$
D.$$\frac{2 \sqrt{3}} {3}$$
3、['空间中直线的方向向量与直线的向量表示'， '用空间向量研究空间中直线、平面的垂直'， '平面的法向量及其应用'， '用空间向量研究空间中直线、平面的平行']正确率60.0%直线$${{l}}$$的一个方向向量为$$( 2， 1， 1 )$$，平面$${{α}}$$的一个法向量为$$( 4， 2， 2 )$$，则（）
B
A.$${{l}{/}{/}{α}}$$
B.$${{l}{⊥}{α}}$$
C.$${{l}{/}{/}{α}}$$或$${{l}{⊂}{α}}$$
D.$${{l}}$$与$${{α}}$$的位置关系不能判断
4、['用空间向量研究直线与平面所成的角'， '用空间向量研究空间中直线、平面的垂直'， '棱柱、棱锥、棱台的体积'， '用空间向量研究空间中直线、平面的平行']正确率40.0%如图，正方体$$A B C D-A_{1} B_{1} C_{1} D_{1}$$的棱长为$${{a}}$$，$${{E}}$$是$${{D}{{D}_{1}}}$$的中点，则（）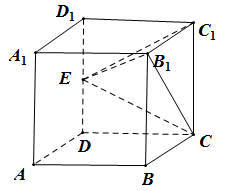
D
A.直线$${{B}_{1}{E}}$$$${{/}{/}}$$平面$${{A}_{1}{B}{D}}$$
B.$$B_{1} E \perp B D_{1}$$
C.三棱锥$$C_{1}-B_{1} C E$$的体积为$$\frac{1} {3} a^{3}$$
D.直线$${{B}_{1}{E}}$$与平面$${{C}{D}{{D}_{1}}{{C}_{1}}}$$所成的角正切值为$$\frac{2 \sqrt{5}} {5}$$
5、['用空间向量研究空间中直线、平面的垂直'， '平面的法向量及其应用'， '用空间向量研究空间中直线、平面的平行']正确率60.0%已知平面$${{α}}$$内的三点$$A ( 0， ~ 0， ~ 1 )， ~ B ( 0， ~ 1， ~ 0 )，$$$$C ( 1， ~ 0， ~ 0 )，$$平面$${{β}}$$的一个法向量为$$n=(-1，-1，-1 )，$$且$${{β}}$$与$${{α}}$$不重合，则（）
A
A.$${{α}{/}{/}{β}}$$
B.$${{α}{⊥}{β}}$$
C.$${{α}}$$与$${{β}}$$相交但不垂直
D.以上都不对
6、['用空间向量研究空间中直线、平面的垂直'， '用空间向量研究空间中直线、平面的平行'， '用空间向量研究两个平面所成的角']正确率60.0%已知$$\overrightarrow{u}=(-2， 2， 0 )， \; \; \overrightarrow{v}=( 6， 6， 4 )， \; \; \overrightarrow{u}， \; \; \overrightarrow{v}$$分别是平面$${{α}{，}{β}}$$的法向量，则平面$${{α}{，}{β}}$$的位置关系是（）
B
A.平行
B.垂直
C.所成的二面角为锐角
D.所成的二面角为钝角
7、['用空间向量研究空间中直线、平面的平行']正确率60.0%已知直线$${{l}}$$的一个方向向量为$$\overrightarrow{m}=(-2，-8， 1 )$$，平面$${{α}}$$的一个法向量为$$\overrightarrow{n}=( x， \frac{1} {2}， 2 )$$，若$${{l}{/}{/}}$$平面$${{α}}$$，则$${{x}{=}}$$（）
C
A.$${{−}{8}}$$
B.$${{8}}$$
C.$${{−}{1}}$$
D.$${{1}}$$
8、['空间中直线的方向向量与直线的向量表示'， '用空间向量研究空间中直线、平面的平行'， '空间向量共线定理']正确率60.0%若两条不重合直线$${{l}_{1}}$$和$${{l}_{2}}$$的方向向量分别为$$\overrightarrow{v_{1}}=( 1， 0，-1 )$$，$$\overrightarrow{v_{2}}=(-2， 0， 2 )$$，则$${{l}_{1}}$$和$${{l}_{2}}$$的位置关系是（）
A
A.平行
B.相交
C.垂直
D.不确定
正确率80.0%若直线$${{l}}$$的方向向量为$$\overrightarrow{a}=( 1， 0， 2 )$$，平面$${{α}}$$的法向量为$$\overrightarrow{n}=(-2， 1， 1 )$$，则$${{(}{)}}$$
C
A.$${{l}{/}{/}{α}}$$
B.$${{l}{⊥}{α}}$$
C.$${{l}{⊂}{α}}$$或$${{l}{/}{/}{α}}$$
D.$${{l}}$$与$${{α}}$$斜交
10、['用空间向量研究空间中直线、平面的平行']正确率40.0%如图，矩形$${{A}{D}{F}{E}}$$、矩形$${{C}{D}{F}{G}}$$、正方形$${{A}{B}{C}{D}}$$两两垂直，且$${{A}{B}{=}{2}}$$，若线段$${{D}{E}}$$上存在点$${{P}}$$，使得$$G P \perp B P$$，则边$${{C}{G}}$$长度的最小值为$${{(}{)}}$$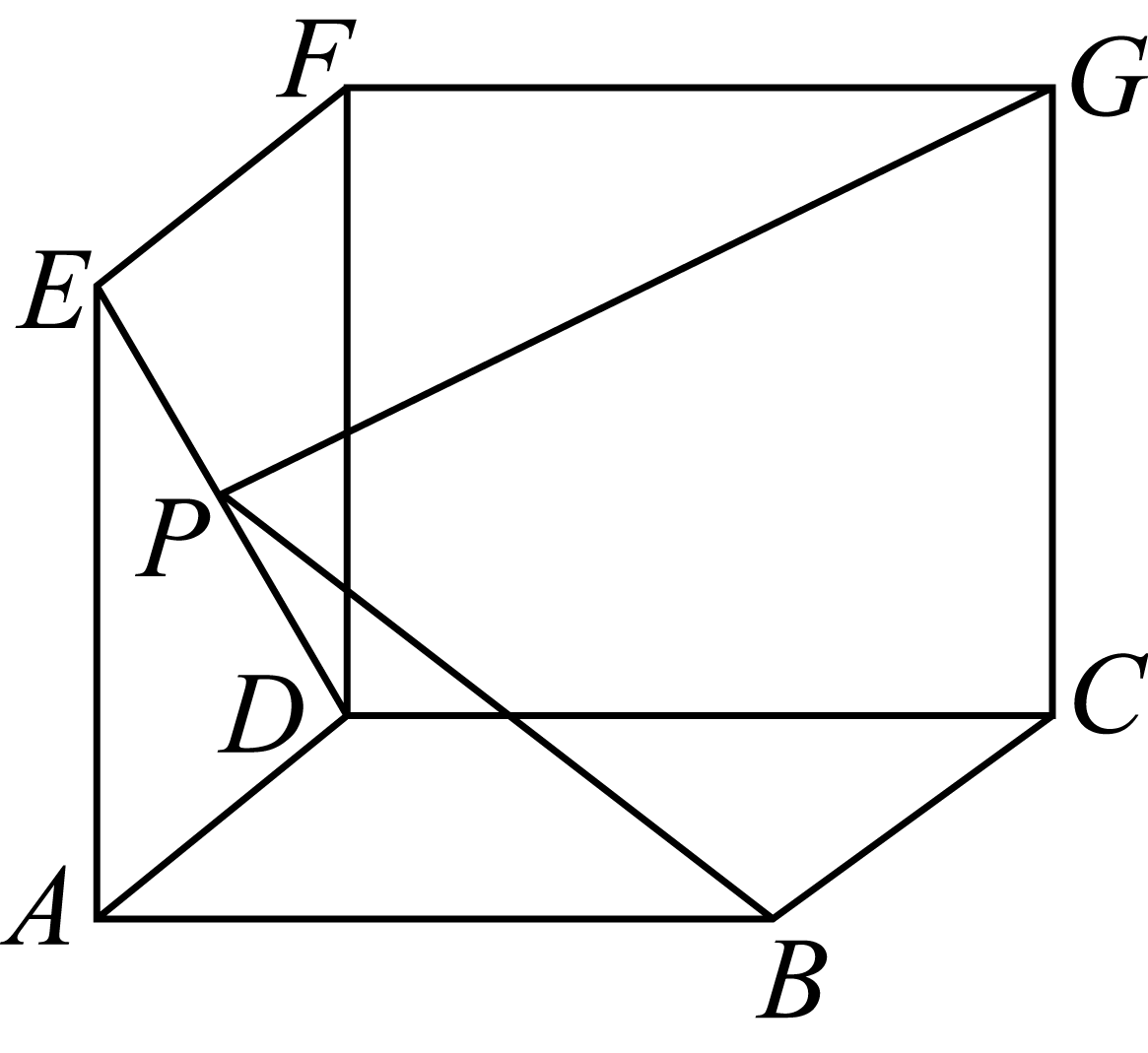
D
A.$${{4}}$$
B.$${{4}{\sqrt {3}}}$$
C.$${{2}}$$
D.$${{2}{\sqrt {3}}}$$
第一题解析：
选项分析：
A. 由于 $$AM$$ 在平面 $$AD_1M$$ 内，而 $$BD$$ 与平面 $$AD_1M$$ 不垂直，故 $$BD \perp AM$$ 不成立。
B. 平面 $$A_1BD$$ 的法向量为 $$(1,1,1)$$，平面 $$AD_1M$$ 的法向量需计算，但验证发现两平面不垂直。
C. 通过向量法证明 $$MN$$ 与平面 $$A_1BD$$ 的法向量垂直，且 $$MN$$ 不在平面内，故 $$MN \parallel$$ 平面 $$A_1BD$$ 成立。
D. $$CM$$ 与平面 $$A_1BD$$ 不平行，故不成立。
正确答案：$$C$$
第二题解析：
建立坐标系，设 $$P(1,1,z)$$，$$Q(x,1-x,0)$$，由 $$PQ \parallel$$ 平面 $$ABC_1D_1$$ 得 $$PQ$$ 与法向量垂直，解得 $$z = x$$。
由 $$PQ \perp RQ$$ 得 $$R$$ 的坐标为 $$(x,0,0)$$，求 $$|PR|$$ 的最小值，通过求导得最小值为 $$\frac{\sqrt{30}}{5}$$。
正确答案：$$B$$
第三题解析：
方向向量 $$(2,1,1)$$ 与法向量 $$(4,2,2)$$ 成比例，故直线与平面平行或直线在平面内。
正确答案：$$C$$
第四题解析：
A. 通过向量法证明 $$B_1E$$ 与平面 $$A_1BD$$ 的法向量垂直，且 $$B_1E$$ 不在平面内，故平行成立。
B. 计算 $$B_1E$$ 与 $$BD_1$$ 的点积为 $$0$$，故垂直成立。
C. 体积计算为 $$\frac{a^3}{6}$$，不成立。
D. 计算正切值为 $$\frac{\sqrt{5}}{5}$$，不成立。
正确答案：$$A, B$$
第五题解析：
平面 $$\alpha$$ 的法向量为 $$(1,1,1)$$，与 $$\beta$$ 的法向量 $$(-1,-1,-1)$$ 成比例，故两平面平行。
正确答案：$$A$$
第六题解析：
计算 $$\overrightarrow{u}$$ 与 $$\overrightarrow{v}$$ 的点积为 $$-12 + 12 + 0 = 0$$，故两平面垂直。
正确答案：$$B$$
第七题解析：
由 $$l \parallel \alpha$$，得 $$\overrightarrow{m} \cdot \overrightarrow{n} = 0$$，解得 $$x = 8$$。
正确答案：$$B$$
第八题解析：
$$\overrightarrow{v_2} = -2\overrightarrow{v_1}$$，故两直线平行。
正确答案：$$A$$
第九题解析：
$$\overrightarrow{a} \cdot \overrightarrow{n} = -2 + 0 + 2 = 0$$，故直线与平面平行或直线在平面内。
正确答案：$$C$$
第十题解析：
建立坐标系，设 $$CG = h$$，由 $$GP \perp BP$$ 得 $$h^2 = 4 + (2-y)^2$$，求最小值得 $$h = 2$$。
正确答案：$$C$$