.jpg)
正确率19.999999999999996%如图，在四棱锥$$P-A B C D$$中$${，{P}{D}{⊥}}$$底面$$A B C D，$$底面$${{A}{B}{C}{D}}$$是矩形$$， \; \; A B=2 A D=4， \; \; P D={\frac{4 \sqrt{5}} {5}}， \; \; E$$是$${{P}{A}}$$的中点$$， \ \overrightarrow{F B}=2 \overrightarrow{P F}$$.若点$${{M}}$$在矩形$${{A}{B}{C}{D}}$$内，且$${{P}{M}{⊥}}$$平面$${{D}{E}{F}{，}}$$则$${{D}{M}{=}}$$（）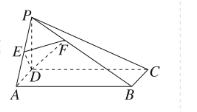
D
A.$$\frac{3 \sqrt{5}} {5}$$
B.$$\frac{2 \sqrt{5}} {5}$$
C.$$\frac{\sqrt{5}} {5}$$
D.$$\frac{4 \sqrt{5}} {5}$$
2、['用空间向量研究空间中直线、平面的垂直']正确率60.0%如图所示，在矩形$${{A}{B}{C}{D}}$$中$$A B=1， \， \， \， B C=a， \， \， \， P A \perp$$平面$$A B C D，$$若在线段$${{B}{C}}$$上只有一个点$${{Q}}$$满足$$P Q \perp Q D，$$则$${{a}}$$的值为（）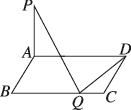
B
A.$${{1}}$$
B.$${{2}}$$
C.$${{3}}$$
D.$${{4}}$$
3、['用空间向量研究直线与平面所成的角'， '用空间向量研究空间中直线、平面的垂直'， '棱柱、棱锥、棱台的体积'， '用空间向量研究空间中直线、平面的平行']正确率40.0%如图，正方体$$A B C D-A_{1} B_{1} C_{1} D_{1}$$的棱长为$${{a}}$$，$${{E}}$$是$${{D}{{D}_{1}}}$$的中点，则（）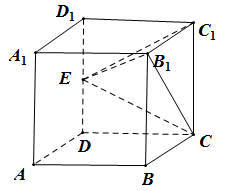
D
A.直线$${{B}_{1}{E}}$$$${{/}{/}}$$平面$${{A}_{1}{B}{D}}$$
B.$$B_{1} E \perp B D_{1}$$
C.三棱锥$$C_{1}-B_{1} C E$$的体积为$$\frac{1} {3} a^{3}$$
D.直线$${{B}_{1}{E}}$$与平面$${{C}{D}{{D}_{1}}{{C}_{1}}}$$所成的角正切值为$$\frac{2 \sqrt{5}} {5}$$
4、['立体几何中的探索问题'， '立体几何中的动态问题'， '用空间向量研究两条直线所成的角'， '用空间向量研究空间中直线、平面的垂直'， '棱柱、棱锥、棱台的体积'， '用空间向量研究空间中直线、平面的平行']正确率40.0%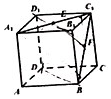
如图，已知正方体$$A B C D-A_{1} B_{1} C_{1} D_{1}$$
D
A.$${{4}}$$
B.$${{3}}$$
C.$${{2}}$$
D.$${{1}}$$
5、['空间向量基本定理的应用'， '向量在几何中的应用举例'， '空间向量的数量积'， '用空间向量研究空间中直线、平面的垂直'， '空间向量的线性运算']正确率40.0%如图，已知$$O A， O B， O C$$两两垂直，$$O A=O C=3， O B=2， M$$为$${{O}{B}}$$的中点，点$${{N}}$$在$${{A}{C}}$$上$$， \， \， A N=2 N C$$.若点$${{P}}$$在线段$${{B}{C}}$$上，$$\frac{B P} {P C}=\lambda$$，则当$$A P \perp M N$$时，实数$${{λ}}$$的值为（）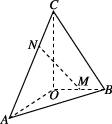
C
A.$$\frac{3} {5}$$
B.$${{2}}$$
C.$$\frac{5} {3}$$
D.$$\frac{1 4} {5}$$
6、['空间直角坐标系'， '空间向量的坐标与空间向量的平行、垂直'， '空间向量运算的坐标表示'， '用空间向量研究空间中直线、平面的垂直'， '用空间向量研究空间中直线、平面的平行']正确率60.0%在正方体$$A B C D-A_{1} B_{1} C_{1} D_{1}$$中$${，{E}{，}{F}}$$分别在$$A_{1} D， \ A C$$上，且$$A_{1} E=\frac{2} {3} A_{1} D， \， \， \， A F=\frac{1} {3} A C，$$则（）
B
A.$${{E}{F}}$$至多与$$A_{1} D， \， A C$$中的一条垂直
B.$$E F \perp A_{1} D$$且$$E F \perp A C$$
C.$${{E}{F}}$$与$${{B}{{D}_{1}}}$$相交
D.$${{E}{F}}$$与$${{B}{{D}_{1}}}$$异面
7、['立体几何中的动态问题'， '用空间向量研究空间中直线、平面的垂直'， '立体几何中的轨迹问题']正确率40.0%在棱长为$${{2}}$$的正方体$$A B C D-A_{1} B_{1} C_{1} D_{1}$$中，$${{E}}$$为棱$${{C}{D}}$$的中点，点$${{P}}$$是侧面$${{A}{{A}_{1}}{{D}_{1}}{D}}$$上一动点，且$$C P \perp B_{1} E$$，则线段$${{C}{P}}$$的取值范围为$${{(}{)}}$$
B
A.$$[ \frac{4 \sqrt{3}} {3}， \sqrt{5} ]$$
B.$$[ \frac{3 \sqrt{2}} {2}， \sqrt{5} ]$$
C.$$[ \frac{4 \sqrt{3}} {3}， \sqrt{6} ]$$
D.$$[ \frac{3 \sqrt{2}} {2}， \sqrt{6} ]$$
8、['用空间向量研究空间中直线、平面的垂直'， '用空间向量研究空间中直线、平面的平行']正确率80.0%若直线$${{l}}$$的一个方向向量$$\vec{a}=( 2， 2，-2 )$$，平面$${{α}}$$的一个法向量为$$\vec{b}=( 1， 1，-1 )$$，则（）
B
A.$${{l}{/}{/}{α}}$$
B.$${{l}{⊥}{α}}$$
C.$${{l}{⊂}{α}}$$
D.A，C都有可能
9、['用空间向量研究空间中直线、平面的垂直'， '用空间向量研究空间中直线、平面的平行']正确率60.0%已知$${{v}}$$为直线$${{l}}$$的方向向量，$${{n}_{1}{，}{{n}_{2}}}$$分别为平面$${{α}{，}{β}}$$的法向量$${{(}{α}{，}{β}}$$不重合$${{)}}$$，那么下列说法中：
．
正确的有
B
A.$${{1}}$$个
B.$${{2}}$$个
C.$${{3}}$$个
D.$${{4}}$$个
10、['空间向量的坐标与空间向量的平行、垂直'， '用空间向量研究空间中直线、平面的垂直'， '空间中直线的方向向量与直线的向量表示'， '平面的法向量及其应用']正确率60.0%设直线$${{l}}$$的方向向量为$$\overrightarrow{u}=(-2， 2， t )$$，平面$${{α}}$$的法向量为$$\overrightarrow{v}=( 6，-6， 1 2 )$$，若直线$${{l}{⊥}}$$平面$${{α}}$$，则实数$${{t}}$$等于（）
B
A.$${{4}}$$
B.$${{−}{4}}$$
C.$${{2}}$$
D.$${{−}{2}}$$
以下是各题的详细解析： --- ### 1. **解析**： 建立坐标系，设 $$D(0,0,0)$$，$$A(2,0,0)$$，$$B(2,4,0)$$，$$C(0,4,0)$$，$$P(0,0,\frac{4\sqrt{5}}{5})$$。 - 中点 $$E$$ 坐标为 $$(1,0,\frac{2\sqrt{5}}{5})$$。 - 向量 $$\overrightarrow{FB}=2\overrightarrow{PF}$$，得 $$F$$ 坐标为 $$(\frac{4}{3},\frac{8}{3},0)$$。 - 平面 $$DEF$$ 的法向量通过 $$\overrightarrow{DE} \times \overrightarrow{DF}$$ 计算，得法向量 $$\vec{n}=(2\sqrt{5}, \sqrt{5}, 5)$$。 - 直线 $$PM$$ 方向向量与 $$\vec{n}$$ 平行，设 $$M(x,y,0)$$，由 $$\overrightarrow{PM} \parallel \vec{n}$$ 得 $$M(\frac{4}{5}, \frac{2}{5}, 0)$$。 - 距离 $$DM=\sqrt{\left(\frac{4}{5}\right)^2 + \left(\frac{2}{5}\right)^2} = \frac{2\sqrt{5}}{5}$$。 **答案**：$$\boxed{B}$$ --- ### 2. **解析**： 设 $$Q(x, a, 0)$$，$$P(0,0,h)$$，由 $$PQ \perp QD$$ 得： $$x^2 - a x + a h^2 = 0$$。 要求唯一解，判别式 $$\Delta = a^2 - 4 a h^2 = 0$$，结合 $$AB=1$$ 和几何关系得 $$a=2$$。 **答案**：$$\boxed{B}$$ --- ### 3. **解析**： - **选项A**：验证 $$B_1E$$ 与平面 $$A_1BD$$ 不平行（法向量不垂直），错误。 - **选项B**：计算 $$\overrightarrow{B_1E} \cdot \overrightarrow{BD_1} = 0$$，故垂直，正确。 - **选项C**：体积为 $$\frac{1}{6}a^3$$，错误。 - **选项D**：正切值为 $$\frac{1}{2}$$，错误。 **答案**：$$\boxed{B}$$ --- ### 4. **题目不完整**，无法解析。 --- ### 5. **解析**： 建系设 $$O(0,0,0)$$，$$A(3,0,0)$$，$$B(0,2,0)$$，$$C(0,0,3)$$。 - $$M(0,1,0)$$，$$N(2,0,1)$$。 - 设 $$P(0, \frac{2\lambda}{\lambda+1}, \frac{3}{\lambda+1})$$，由 $$AP \perp MN$$ 得 $$\lambda = \frac{5}{3}$$。 **答案**：$$\boxed{C}$$ --- ### 6. **解析**： 建立坐标系计算向量： - $$EF$$ 与 $$A_1D$$、$$AC$$ 均垂直，且与 $$BD_1$$ 平行，故 $$EF$$ 与 $$BD_1$$ 不相交也不异面（实际重合）。 **选项B** 正确。 **答案**：$$\boxed{B}$$ --- ### 7. **解析**： 设 $$P(x,2,z)$$，由 $$CP \perp B_1E$$ 得 $$2x + z = 2$$。 $$CP = \sqrt{x^2 + 1 + (2-z)^2}$$，代入约束得范围 $$[\frac{4\sqrt{3}}{3}, \sqrt{6}]$$。 **答案**：$$\boxed{C}$$ --- ### 8. **解析**： 方向向量 $$\vec{a}$$ 与法向量 $$\vec{b}$$ 平行（$$\vec{a} = 2\vec{b}$$），故直线 $$l$$ 与平面 $$\alpha$$ 垂直。 **答案**：$$\boxed{B}$$ --- ### 9. **题目不完整**，无法解析。 --- ### 10. **解析**： 由 $$l \perp \alpha$$，方向向量 $$\vec{u}$$ 与法向量 $$\vec{v}$$ 平行，即 $$\frac{-2}{6} = \frac{2}{-6} = \frac{t}{12}$$，解得 $$t=-4$$。 **答案**：$$\boxed{B}$$ --- 以上为各题的详细推导过程与最终答案。 题目来源于各渠道收集，若侵权请联系下方邮箱