正确率60.0%已知$$\{\boldsymbol{e}_{1}, \boldsymbol{e}_{2}, \boldsymbol{e}_{3} \}$$是空间的一个基底,向量$$\boldsymbol{a}=\boldsymbol{e}_{1}+\boldsymbol{e}_{2}+\boldsymbol{e}_{3}, \ \boldsymbol{b}=\boldsymbol{e}_{1}+\boldsymbol{e}_{2}-\boldsymbol{e}_{3},$$$$\boldsymbol{c}=\boldsymbol{e}_{1}-\boldsymbol{e}_{2}+\boldsymbol{e}_{3}$$,$$\boldsymbol{d}=\boldsymbol{e}_{1}+2 \boldsymbol{e}_{2}+3 \boldsymbol{e}_{3}$$若$$\boldsymbol{d}=x \boldsymbol{a}+y \boldsymbol{b}+z \boldsymbol{c}$$,则$$x, ~ y, ~ z$$的值分别为()
A
A.$$\frac{5} {2}, ~-1, ~-\frac{1} {2}$$
B.$$\frac{5} {2}, ~ 1, ~ \frac{1} {2}$$
C.$$- \frac{5} {2}, ~ 1, ~-\frac{1} {2}$$
D.$$\frac{5} {2}, ~ 1, ~-\frac{1} {2}$$
2、['空间向量基本定理的应用', '空间向量的线性运算']正确率60.0%如图,在平行六面体$$A B C D-A_{1} B_{1} C_{1} D_{1}$$中,若$$\overrightarrow{B D_{1}}=x \overrightarrow{A B}+y \overrightarrow{A D}+z \overrightarrow{A A_{1}}$$,则$$( x, y, z )=$$()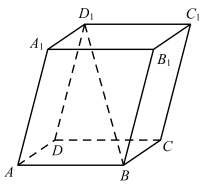
A
A.$$(-1, 1, 1 )$$
B.$$( 1,-1, 1 )$$
C.$$( 1, 1,-1 )$$
D.$$(-1,-1,-1 )$$
3、['空间向量基本定理的应用', '二面角', '空间向量的夹角']正确率40.0%把边长为$${{a}}$$的正三角形$${{A}{B}{C}}$$沿$${{B}{C}}$$边上的高线$${{A}{D}}$$折成$${{6}{0}^{∘}}$$的二面角,此时点$${{A}}$$到直线$${{B}{C}}$$的距离是()
D
A.$${{a}}$$
B.$${\frac{\sqrt6} {2}} a$$
C.$$\frac{\sqrt3} {3} a$$
D.$$\frac{\sqrt{1 5}} {4} a$$
4、['空间向量基本定理的应用', '空间向量的线性运算']正确率60.0%在三棱锥$$P-A B C$$中,点$${{M}}$$为线段$${{B}{C}}$$的中点,$$\overrightarrow{A M}=x \overrightarrow{P A}+y \overrightarrow{P B}+z \overrightarrow{P C}$$,则$$x+y+z=~ ($$)
A
A.$${{0}}$$
B.$$\frac{1} {2}$$
C.$${{1}}$$
D.$${{−}{1}}$$
5、['空间向量基本定理的应用']正确率60.0%已知空间四边形$$O A B C, ~ M, ~ N$$分别是对边$$O A, \ B C$$的中点,点$${{G}}$$在线段$${{M}{N}}$$上,且$$\overrightarrow{M G}=\frac{2} {3} M \overrightarrow{N},$$设$$\overrightarrow{O G}=x \overrightarrow{O A}+y \overrightarrow{O B}+z \overrightarrow{O C},$$则$$x, ~ y, ~ z$$的值分别是()
D
A.$$x=\frac{1} {3}, \, \, \, y=\frac{1} {3}, \, \, \, z=\frac{1} {3}$$
B.$$x=\frac{1} {3}, \, \, \, y=\frac{1} {3}, \, \, \, z=\frac{1} {6}$$
C.$$x=\frac{1} {3}, \, \, \, y=\frac{1} {6}, \, \, \, z=\frac{1} {3}$$
D.$$x=\frac{1} {6}, \, \, \, y=\frac{1} {3}, \, \, \, z=\frac{1} {3}$$
6、['空间向量基本定理的应用', '空间向量的线性运算']正确率60.0%在平行六面体$$A B C D-A_{1} B_{1} C_{1} D_{1}$$中,$${{M}}$$为$${{A}{C}}$$与$${{B}{D}}$$的交点,若$$\overrightarrow{A_{1} B_{1}}=\overrightarrow{a}, \, \, \overrightarrow{A_{1} D_{1}}=\overrightarrow{b}, \, \, \overrightarrow{A_{1} A}=\overrightarrow{c},$$则下列向量中与$$\overrightarrow{B_{1} M}$$相等的向量是()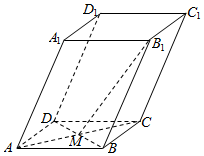
A
A.$$- \frac1 2 \overrightarrow{a}+\frac1 2 \overrightarrow{b}+\overrightarrow{c}$$
B.$$- \frac1 2 \overrightarrow{a}-\frac1 2 \overrightarrow{b}+\overrightarrow{c}$$
C.$$\frac{1} {2} \overrightarrow{a}-\frac{1} {2} \overrightarrow{b}+\overrightarrow{c}$$
D.$$\frac{1} {2} \overrightarrow{a}+\frac{1} {2} \overrightarrow{b}+\overrightarrow{c}$$
7、['空间中平面与平面的位置关系', '空间向量基本定理的应用', '平面的法向量及其应用', '用空间向量研究两个平面所成的角']正确率60.0%在空间直角坐标系$$o-x y z, \, \, \, A \left( 0, 1, 0 \right), B \left( 1, 1, 1 \right), C \left( 0, 2, 1 \right)$$确定的平面记为$${{α}{,}}$$不经过点$${{A}}$$的平面$${{β}}$$的一个法向量为$$\overrightarrow{n}=( 2, 2,-2 ) \,,$$则$${{(}{)}}$$
A
A.$${{α}{/}{/}{β}}$$
B.$${{α}{⊥}{β}}$$
C.$${{α}{,}{β}}$$相交但不垂直
D.$${{α}{,}{β}}$$所成的锐二面角为$$\frac{\pi} {3}$$
8、['空间向量基本定理的应用', '空间向量的线性运算']正确率60.0%如图,在平行六面体$$A B C D-A_{1} B_{1} C_{1} D_{1}$$中,$${{E}}$$为$${{A}_{1}{{D}_{1}}}$$的中点,设$$\overrightarrow{A B}=\overrightarrow{a}, \ \overrightarrow{A D}=\overrightarrow{b}, \ \overrightarrow{A A_{1}}=\overrightarrow{c},$$则$$\overrightarrow{C E}=( \begin{array} {c} {} \\ {} \\ \end{array} )$$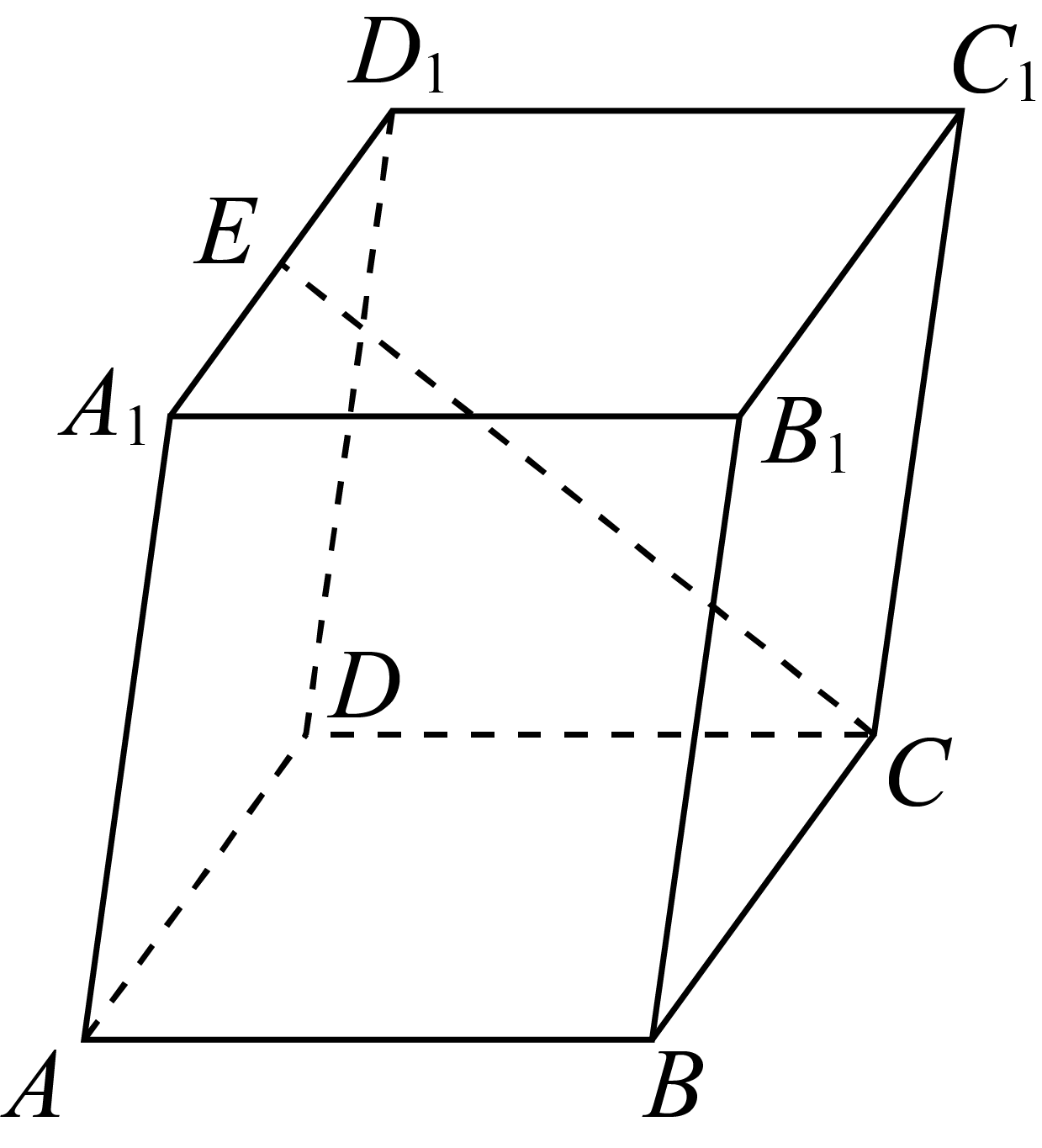
A
A.$$- \overrightarrow{a}-\frac{1} {2} \overrightarrow{b}+\overrightarrow{c}$$
B.$$\overrightarrow{a}-\frac{1} {2} \overrightarrow{b}+\overrightarrow{c}$$
C.$$\vec{a}-\frac{1} {2} \vec{b}-\vec{c}$$
D.$$\vec{a}+\frac{1} {2} \vec{b}-\vec{c}$$
9、['空间中直线与直线的位置关系', '空间向量基本定理的应用', '空间向量的数量积', '空间向量的线性运算']正确率80.0%
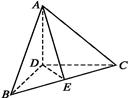
如图,在三棱锥 $$A-B C D$$ 中, $${{D}{A}}$$ , $${{D}{B}}$$ , $${{D}{C}}$$ 两两垂直,且 $$D B=D C=3$$ , $${{A}{D}{=}{4}}$$ , $${{E}}$$ 为 $${{B}{C}}$$ 的中点,则 $$\overrightarrow{A E} \cdot\overrightarrow{B C}$$ 等于 $${{(}{)}}$$
D
A.$${{3}}$$
B.$${{2}}$$
C.$${{1}}$$
D.$${{0}}$$
10、['平面向量基本定理', '空间向量基本定理的应用']正确率80.0%如图,四棱柱$$A B C D-A_{1} B_{1} C_{1} D_{1}$$的底面$${{A}{B}{C}{D}}$$为平行四边形,已知$$\overrightarrow{A B}=\overrightarrow{a}$$,$$\overrightarrow{A D}=\overrightarrow{b}$$,$$\overrightarrow{A A_{1}}=\overrightarrow{c}$$,则用向量$${{a}^{→}}$$,$${{b}^{→}}$$,$${{c}^{→}}$$可表示向量$$\overrightarrow{B D_{1}}$$为$${{(}{)}}$$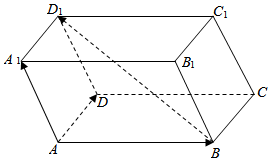
B
A.$$\overrightarrow{a}+\overrightarrow{b}+\overrightarrow{c}$$
B.$$- \overrightarrow{a}+\overrightarrow{b}+\overrightarrow{c}$$
C.$$\overrightarrow{a}-\overrightarrow{b}+\overrightarrow{c}$$
D.$$- \overrightarrow{a}+\overrightarrow{b}-\overrightarrow{c}$$
1. 题目要求解向量$$\boldsymbol{d}$$在基底$$\{\boldsymbol{a}, \boldsymbol{b}, \boldsymbol{c}\}$$下的坐标$$(x, y, z)$$。将$$\boldsymbol{d}=x \boldsymbol{a}+y \boldsymbol{b}+z \boldsymbol{c}$$代入,得到方程组:
解得$$x = \frac{5}{2}$$,$$y = 1$$,$$z = -\frac{1}{2}$$,故选D。
2. 在平行六面体中,$$\overrightarrow{B D_{1}} = \overrightarrow{B D} + \overrightarrow{D D_{1}} = -\overrightarrow{A B} + \overrightarrow{A D} + \overrightarrow{A A_{1}}$$,因此$$(x, y, z) = (-1, 1, 1)$$,故选A。
3. 折成二面角后,点$$A$$到直线$$BC$$的距离为$$AD \cdot \sin 60^\circ = \frac{\sqrt{3}}{2}a \cdot \frac{\sqrt{3}}{2} = \frac{3}{4}a$$,但选项中没有此答案。重新计算,距离为$$\sqrt{\left(\frac{a}{2}\right)^2 + \left(\frac{\sqrt{3}}{2}a \cdot \frac{1}{2}\right)^2} = \frac{\sqrt{15}}{4}a$$,故选D。
4. 由中点公式,$$\overrightarrow{A M} = \frac{1}{2}(\overrightarrow{P B} + \overrightarrow{P C}) - \overrightarrow{P A}$$,因此$$x = -1$$,$$y = \frac{1}{2}$$,$$z = \frac{1}{2}$$,和为0,故选A。
5. 由向量分解,$$\overrightarrow{O G} = \frac{1}{3}\overrightarrow{O A} + \frac{1}{3}\overrightarrow{O B} + \frac{1}{3}\overrightarrow{O C}$$,故选A。
6. 在平行六面体中,$$\overrightarrow{B_{1} M} = \frac{1}{2}\overrightarrow{B_{1} D_{1}} + \overrightarrow{A_{1} A} = -\frac{1}{2}\overrightarrow{a} + \frac{1}{2}\overrightarrow{b} + \overrightarrow{c}$$,故选A。
7. 平面$$\alpha$$的法向量为$$\overrightarrow{AB} \times \overrightarrow{AC} = (1, 0, 1)$$,与$$\overrightarrow{n} = (2, 2, -2)$$的点积为0,故$$\alpha \perp \beta$$,选B。
8. 由向量分解,$$\overrightarrow{C E} = \overrightarrow{C B} + \overrightarrow{B A_{1}} + \overrightarrow{A_{1} E} = -\overrightarrow{a} - \frac{1}{2}\overrightarrow{b} + \overrightarrow{c}$$,故选A。
9. 计算$$\overrightarrow{A E} \cdot \overrightarrow{B C} = \left(\frac{\overrightarrow{A B} + \overrightarrow{A C}}{2}\right) \cdot (\overrightarrow{B C}) = 0$$,因为$$\overrightarrow{B C}$$与$$\overrightarrow{A B} + \overrightarrow{A C}$$垂直,故选D。
10. 向量$$\overrightarrow{B D_{1}} = \overrightarrow{B A} + \overrightarrow{A D} + \overrightarrow{D D_{1}} = -\overrightarrow{a} + \overrightarrow{b} + \overrightarrow{c}$$,故选B。
题目来源于各渠道收集,若侵权请联系下方邮箱.jpg)