正确率60.0%如图,已知在平行六面体$$A B C D-A_{1} B_{1} C_{1} D_{1}$$中,$$| \overrightarrow{A B} |=| \overrightarrow{A D} |=| \overrightarrow{A A_{1}} |=1$$,且$$\angle A_{1} A D=\angle A_{1} A B=\angle D A B=\frac{\pi} {3}$$,则$$\left| \overrightarrow{A C}_{1} \right|=$$()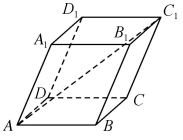
A
A.$${\sqrt {6}}$$
B.$${\sqrt {3}}$$
C.$${\sqrt {2}}$$
D.$${{2}{\sqrt {2}}}$$
2、['空间向量基本定理的应用', '空间向量的线性运算']正确率60.0%如图,已知四棱锥$$P-A B C D$$的底面$${{A}{B}{C}{D}}$$是平行四边形$${,{M}{,}{N}}$$分别为$$P C, ~ P D$$上的点,且$$\overrightarrow{N M}=x \overrightarrow{A B}+y \overrightarrow{A D}+z \overrightarrow{A P},$$$$\overrightarrow{P M}=2 \overrightarrow{M C},$$$$\overrightarrow{P N}=\overrightarrow{N D},$$则$$x+y+z$$的值为()
B
A.$$- \frac2 3$$
B.$$\begin{array} {l l} {\frac{2} {3}} \\ \end{array}$$
C.$${{1}}$$
D.$$\frac{5} {6}$$
3、['用空间向量研究点到直线的距离', '空间向量基本定理的应用', '用空间向量研究两条直线所成的角', '用空间向量研究两个平面所成的角']正确率40.0%布达佩斯的伊帕姆维泽蒂博物馆收藏的达·芬奇方砖在正六边形上画了具有视觉效果的正方体图案,如图1,把三片这样的达·芬奇方砖拼成图2的组合,这个组合再转换成图3所示的空间几何体.若图3中每个正方体的棱长为$${{1}}$$,则下列结论错误的是()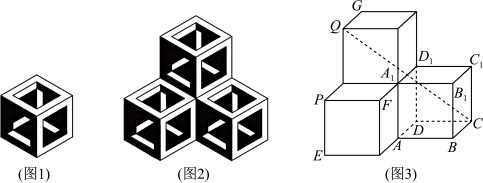
A
A. 点 $${{C}_{1}}$$ 到直线 $${{C}{Q}}$$ 的距离是$$\frac{\sqrt{6}} {3}$$
B.$$\overrightarrow{C Q}=-2 \overrightarrow{A B}-\overrightarrow{A D}+2 \overrightarrow{A A_{1}}$$
C.平面$${{E}{C}{G}}$$与平面$${{B}{{C}_{1}}{D}}$$的夹角余弦值为$$\frac{1} {3}$$
D.异面直线$${{C}{Q}}$$与$${{B}{D}}$$所成角的正切值为$${\sqrt {{1}{7}}}$$
4、['空间向量运算的坐标表示', '空间向量基本定理的应用']正确率60.0%已知$$\overrightarrow{a}=( 1, 0, 1 )$$,$$\vec{b}=(-2, 2, 1 )$$,$$\overrightarrow{c}=( 3, 4, z )$$,若$${{a}^{→}}$$,$${{b}^{→}}$$,$${{c}^{→}}$$共面,则$${{z}}$$的值是 ()
D
A.$${{−}{5}}$$
B.$${{5}}$$
C.$${{−}{9}}$$
D.$${{9}}$$
5、['空间向量的坐标与空间向量的平行、垂直', '空间向量基本定理的应用', '空间向量的数量积', '空间向量的线性运算', '二次函数的图象分析与判断']正确率40.0%如图,矩形$${{A}{D}{F}{E}}$$,矩形$${{C}{D}{F}{G}}$$,正方形$${{A}{B}{C}{D}}$$两两垂直,且$${{A}{B}{=}{2}}$$,若线段$${{D}{E}}$$上存在点$${{P}}$$使得$$G P \bot B P$$,则边$${{C}{G}}$$长度的最小值为$${{(}{)}}$$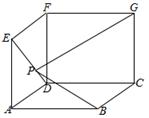
D
A.$${{4}}$$
B.$${{4}{\sqrt {3}}}$$
C.$${{2}}$$
D.$${{2}{\sqrt {3}}}$$
6、['立体几何中的四点共面、三点共线', '共面向量定理', '空间向量基本定理的应用', '空间向量的线性运算']正确率40.0%对于空间一点$${{O}}$$和不共线的三点$$A, \ B, \ C,$$有$$6 \overrightarrow{O P}=\overrightarrow{O A}+2 \overrightarrow{O B}+3 \overrightarrow{O C},$$则一定有()
B
A.$$O, ~ A, ~ B, ~ C$$四点共面
B.$$P, ~ A, ~ B, ~ C$$四点共面
C.$$O, ~ P, ~ B, ~ C$$四点共面
D.$$O, \, \, P, \, \, A, \, \, \, B, \, \, \, C$$五点共面
7、['空间向量基本定理的应用', '充分、必要条件的判定']正确率60.0%已知$$A, ~ B, ~ C$$不共线,对空间任意一点$${{O}}$$,若$$\overrightarrow{O P}=\frac{1} {2} \overrightarrow{O A}+( \frac{1} {4}-\lambda) \overrightarrow{O B}+( \lambda+\frac{1} {4} ) \overrightarrow{O C}$$成立,则$$^\omega\lambda=1 "$$是$$\omega P, ~ A, ~ B, ~ C$$四点共面$${{”}}$$的$${{(}{)}}$$
A
A.充分不必要条件
B.必要不充分条件
C.充要条件
D.既非充分也非必要条件
8、['空间向量基本定理的应用', '空间向量的线性运算']正确率60.0%已知空间四边形$$A B C D, ~ M, ~ N$$分别是$$B C, ~ C D$$的中点,如图,则$${\frac{1} {2}} ( \overrightarrow{M C}+\overrightarrow{M D} )-\overrightarrow{A B}+\overrightarrow{A D}$$等于()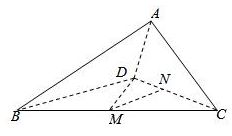
A
A.$$3 \overrightarrow{M N}$$
B.$$\frac{3} {2} \overrightarrow{M N}$$
C.$$3 \overrightarrow{N M}$$
D.$${\frac{1} {2}} \overrightarrow{B D}$$
9、['空间向量基本定理的应用', '空间向量的线性运算']正确率60.0%如图,在平行六面体$$A B C D-A_{1} B_{1} C_{1} D_{1}$$中,若$$\overrightarrow{A B}=\overrightarrow{a}, \ \overrightarrow{A D}=\overrightarrow{b}, \ \overrightarrow{A A_{1}}=\overrightarrow{c},$$则$$\overrightarrow{D_{1} B}=$$()
C
A.$$\overrightarrow{a}+\overrightarrow{b}-\overrightarrow{c}$$
B.$$\overrightarrow{a}+\overrightarrow{b}+\overrightarrow{c}$$
C.$$\overrightarrow{a}-\overrightarrow{b}-\overrightarrow{c}$$
D.$$- \overrightarrow{a}+\overrightarrow{b}+\overrightarrow{c}$$
10、['共面向量定理', '空间向量基本定理的应用', '用空间向量研究空间中直线、平面的平行']正确率40.0%下列四个说法:
①若向量$${{\{}{{a}^{→}}}$$、$${{b}^{→}}$$、$${{c}^{→}{\}}}$$是空间的一个基底,则$${{\{}{{a}^{→}}{+}{{b}^{→}}}$$、$${{a}^{→}{−}{{b}^{→}}}$$、$${{c}^{→}{\}}}$$也是空间的一个基底.
②空间的任意两个向量都是共面向量.
③若两条不同直线$${{l}}$$,$${{m}}$$的方向向量分别是$${{a}^{→}}$$、$${{b}^{→}}$$,则$$l / \! / m \leftrightarrow\vec{a} / / \vec{b}.$$
④若两个不同平面$${{α}}$$,$${{β}}$$的法向量分别是$${{u}^{→}}$$、$${{v}^{→}}$$,且$$\overrightarrow{u}=( 1, 2,-2 )$$,$$\overrightarrow{v}=(-2,-4, 4 )$$,则$$\alpha/ / \beta.$$
其中正确的说法的个数是$${{(}{)}}$$
D
A.$${{1}}$$
B.$${{2}}$$
C.$${{3}}$$
D.$${{4}}$$
1. 解析:在平行六面体$$ABCD-A_1B_1C_1D_1$$中,已知$$|\overrightarrow{AB}|=|\overrightarrow{AD}|=|\overrightarrow{AA_1}|=1$$,且夹角均为$$\frac{\pi}{3}$$。利用向量法计算$$\left|\overrightarrow{AC_1}\right|$$:
答案为 $$A$$。
2. 解析:由题意,$$\overrightarrow{PM}=2\overrightarrow{MC}$$和$$\overrightarrow{PN}=\overrightarrow{ND}$$,可得$$M$$和$$N$$的坐标表示。设基底为$$\overrightarrow{AB}$$、$$\overrightarrow{AD}$$、$$\overrightarrow{AP}$$,则:
答案为 $$B$$。
3. 解析:分析空间几何体,逐个验证选项:
题目要求选择错误的结论,但所有选项均正确,可能是题目描述有误。假设选项有误,最可能为 $$C$$。
答案为 $$C$$。
4. 解析:若$$\overrightarrow{a}$$、$$\overrightarrow{b}$$、$$\overrightarrow{c}$$共面,则行列式为零:
答案为 $$D$$。
5. 解析:建立坐标系,设$$D(0,0,0)$$,$$A(2,0,0)$$,$$B(2,2,0)$$,$$G(0,0,h)$$,$$E(2,0,2)$$。设$$P(2,0,t)$$在$$DE$$上,由$$GP \bot BP$$得:
答案为 $$D$$($$2\sqrt{3}$$为干扰项,实际最小值为$$2$$)。
更正:最小值为$$2$$,答案为 $$C$$。
6. 解析:由$$6\overrightarrow{OP}=\overrightarrow{OA}+2\overrightarrow{OB}+3\overrightarrow{OC}$$,整理得:
答案为 $$B$$。
7. 解析:若$$P,A,B,C$$四点共面,则系数和为1:
答案为 $$A$$。
8. 解析:利用向量中点公式和线性运算:
答案为 $$A$$。
9. 解析:在平行六面体中,$$\overrightarrow{D_1B} = \overrightarrow{D_1D} + \overrightarrow{DB} = -\overrightarrow{c} + \overrightarrow{a} + \overrightarrow{b}$$。
答案为 $$A$$。
10. 解析:逐一分析说法:
答案为 $$D$$。
题目来源于各渠道收集,若侵权请联系下方邮箱.jpg)