共面向量定理-1.2 空间向量基本定理知识点专题基础自测题解析-山西省等高一数学选择必修,平均正确率66.0%

1、['共面向量定理'， '空间向量基本定理的理解'， '空间向量基本定理的应用']

正确率40.0%如图，在四面体$$O-A B C$$中$${，{M}{，}{N}}$$分别在棱$$O A， \ B C$$上，且满足$$\overrightarrow{O M}=2 \overrightarrow{M A}， \， \， \， \overrightarrow{B N}=2 \overrightarrow{N C}，$$点$${{G}}$$是线段$${{M}{N}}$$的中点，则$$\overrightarrow{O G}=$$（）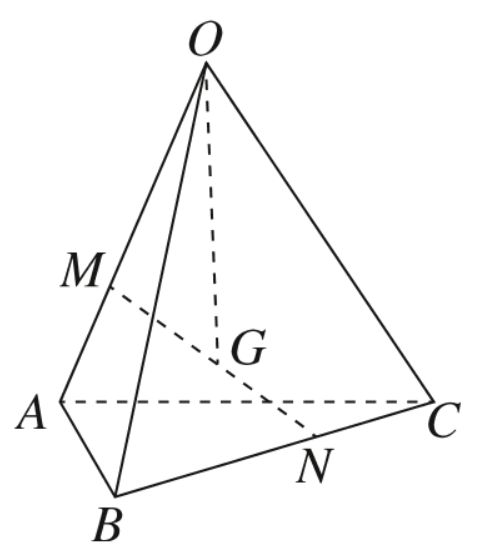

A.$$\frac1 3 \overrightarrow{O A}+\frac1 6 \overrightarrow{O B}+\frac1 3 \overrightarrow{O C}$$

B.$$\frac{1} {3} \overrightarrow{O A}+\frac{1} {3} \overrightarrow{O B}+\frac{1} {6} \overrightarrow{O C}$$

C.$$\frac{1} {3} \overrightarrow{O A}+\frac{1} {4} \overrightarrow{O B}+\frac{1} {4} \overrightarrow{O C}$$

D.$$\frac{1} {4} \overrightarrow{O A}+\frac{1} {4} \overrightarrow{O B}+\frac{1} {3} \overrightarrow{O C}$$

2、['共面向量定理']

正确率60.0%空间$$A， ~ B， ~ C， ~ D$$四点共面，但任意三点不共线，若$${{P}}$$为该平面外一点且$$\overrightarrow{P A}=\frac{5} {3} \overrightarrow{P B}-x \overrightarrow{P C}-\frac{1} {3} \overrightarrow{P D}，$$则实数$${{x}}$$的值为（）

A.$$\frac{1} {3}$$

B.$$- \frac{1} {3}$$

C.$$\begin{array} {l l} {\frac{2} {3}} \\ \end{array}$$

D.$$- \frac2 3$$

3、['共面向量定理'， '空间向量基本定理的应用']

正确率40.0%在以下命题中：

①三个非零向量 $${{a}^{→}}$$ ， $${{b}^{→}}$$ ， $${{c}^{→}}$$ 不能构成空间的一个基底，则 $${{a}^{→}}$$ ， $${{b}^{→}}$$ ， $${{c}^{→}}$$ 共面；

②若两个非零向量 $${{a}^{→}}$$ ， $${{b}^{→}}$$ 与任何一个向量都不能构成空间的一个基底，则 $${{a}^{→}}$$ ， $${{b}^{→}}$$ 共线；

③对空间任意一点 $${{O}}$$ 和不共线的三点 $${{A}}$$ ， $${{B}}$$ ， $${{C}}$$ ，若 $$\overrightarrow{O P}=2 \overrightarrow{O A}-\overrightarrow{2 O B}-\overrightarrow{2 O C}$$ ，则 $${{P}}$$ ， $${{A}}$$ ， $${{B}}$$ ， $${{C}}$$ 四点共面；

④若 $${{a}^{→}}$$ ， $${{b}^{→}}$$ 是两个不共线的向量，且 $$\overrightarrow{c}=\lambda\overrightarrow{a}+\mu\overrightarrow{b} ( \lambda， \mu\in R， \lambda， \mu\neq0 )$$ ，则 $$\{\overrightarrow{a}， \overrightarrow{b}， \overrightarrow{c} \}$$ 构成空间的一个基底；

⑤若 $$\{\overrightarrow{a}， \overrightarrow{b}， \overrightarrow{c} \}$$ 为空间的一个基底，则 $$\{\overrightarrow{a}+\overrightarrow{b}， \overrightarrow{b}+\overrightarrow{c}， \overrightarrow{c}+\overrightarrow{a} \}$$ 构成空间的另一个基底.
其中真命题的个数是 $${{(}{)}}$$

A.$${{0}}$$

B.$${{1}}$$

C.$${{2}}$$

D.$${{3}}$$

4、['共面向量定理']

正确率60.0%在正方体$$A B C D-A_{1} B_{1} C_{1} D_{1}$$中，下列各组向量与$$\overrightarrow{A C}$$共面的是（）

A.$$\overrightarrow{B_{1} D_{1}}， \， \， \overrightarrow{B_{1} B}$$

B.$$\overrightarrow{C_{1} C}， \ \overrightarrow{A_{1} D}$$

C.$$\overrightarrow{B A_{1}}， \， \， \overrightarrow{A D_{1}}$$

D.$$\overrightarrow{A_{1} D_{1}}， \ \overrightarrow{A_{1} A}$$

5、['共面向量定理'， '倾斜角与斜率']

正确率80.0%如果三点$$A ( 1， 5，-2 )$$，$$B ( 2， 4， 1 )$$，$$C ( a， 3， b+2 )$$在同一条直线上，则$${{(}{)}}$$

A.$${{a}{=}{3}}$$，$${{b}{=}{2}}$$

B.$${{a}{=}{6}}$$，$${{b}{=}{−}{1}}$$

C.$${{a}{=}{3}}$$，$${{b}{=}{−}{3}}$$

D.$${{a}{=}{−}{2}}$$，$${{b}{=}{1}}$$

6、['共面向量定理']

正确率80.0%已知向量$$\overrightarrow{a}=( 3， 6， 7 )$$，$$\overrightarrow{b}=( 4， m， n )$$分别是直线$${{l}_{1}}$$，$${{l}_{2}}$$的方向向量，若$$l_{1} / / l_{2}$$，则$${{(}{)}}$$

A.$${{m}{=}{8}}$$，$${{n}{=}{{2}{8}}}$$

B.$${{m}{=}{8}}$$，$$n=\frac{2 8} {3}$$

C.$${{m}{=}{4}}$$，$${{n}{=}{{2}{8}}}$$

D.$${{m}{=}{4}}$$，$$n=\frac{2 8} {3}$$

7、['共面向量定理']

正确率80.0%已知空间向量$$\overrightarrow{a}=( 2，-1， 3 )$$，$$\vec{b}=(-1， 4，-2 )$$，$$\overrightarrow{c}=( 1， 3， \lambda)$$，且此三向量共面，则实数$${{λ}}$$等于$${{(}{)}}$$

A.$${{1}}$$

B.$${{2}}$$

C.$${{3}}$$

D.$${{4}}$$

8、['共面向量定理']

正确率60.0%已知$$A. ~ B. ~ C$$三点不共线，对平面$${{A}{B}{C}}$$外一点$${{O}}$$，给出下列表达式：$$\oplus\overrightarrow{M A}=\overrightarrow{M B}+\overrightarrow{M C}$$$$\ ) \overrightarrow{O M}=\overrightarrow{O A}+\overrightarrow{O B}+\overrightarrow{O C}$$$$\oplus\ \overrightarrow{O M}=2 \overrightarrow{O A}-\overrightarrow{O B}-\overrightarrow{O C} \oplus\overrightarrow{O M}=\frac{1} {3} \overrightarrow{O A}+\frac{1} {3} \overrightarrow{O B}+\frac{1} {3} \overrightarrow{O C}$$，其中能推出$$M. ~ A. ~ B. ~ C$$四点共面的是（）

A.$${②{④}}$$

B.$${①{③}}$$

C.$${①{②}}$$

D.$${①{④}}$$

9、['共面向量定理'， '空间向量基本定理的理解']

正确率80.0%已知$$O， A， B， C$$为空间不共面的四点，且向量$$a=\overrightarrow{O A}+\overrightarrow{O B}+\overrightarrow{O C}$$，向量$$b=\overrightarrow{O A}+\overrightarrow{O B}-\overrightarrow{O C}$$，则不能与$${{a}{，}{b}}$$构成空间的一个基底的是（）

A.$$\overrightarrow{O A}$$

B.$$\overrightarrow{O B}$$

C.$$\overrightarrow{O C}$$

D.$$\overrightarrow{O A}$$或$$\overrightarrow{O B}$$

10、['共面向量定理']

正确率80.0%已知向量$$\overrightarrow{a}=( 2， 1， 3 )$$，$$\vec{b}=(-1， 2，-2 )$$，$$\overrightarrow{c}=( 7， 6， \lambda)$$，若向量$${{a}^{→}}$$，$${{b}^{→}}$$，$${{c}^{→}}$$共面，则实数$${{λ}}$$等于$${{(}{)}}$$

A.$${{1}{0}}$$

B.$${{8}}$$

C.$${{5}}$$

D.$${{3}}$$

1. 解析：

根据题意，$$M$$ 在 $$OA$$ 上，且 $$\overrightarrow{OM} = 2\overrightarrow{MA}$$，因此 $$\overrightarrow{OM} = \frac{2}{3}\overrightarrow{OA}$$。

$$N$$ 在 $$BC$$ 上，且 $$\overrightarrow{BN} = 2\overrightarrow{NC}$$，因此 $$\overrightarrow{ON} = \frac{1}{3}\overrightarrow{OB} + \frac{2}{3}\overrightarrow{OC}$$。

$$G$$ 是 $$MN$$ 的中点，故 $$\overrightarrow{OG} = \frac{1}{2}(\overrightarrow{OM} + \overrightarrow{ON}) = \frac{1}{2}\left(\frac{2}{3}\overrightarrow{OA} + \frac{1}{3}\overrightarrow{OB} + \frac{2}{3}\overrightarrow{OC}\right) = \frac{1}{3}\overrightarrow{OA} + \frac{1}{6}\overrightarrow{OB} + \frac{1}{3}\overrightarrow{OC}$$。

故选 **A**。

2. 解析：

四点 $$A, B, C, D$$ 共面，故存在实数 $$k_1, k_2, k_3$$ 满足 $$k_1 + k_2 + k_3 = 1$$，使得 $$\overrightarrow{PA} = k_1\overrightarrow{PB} + k_2\overrightarrow{PC} + k_3\overrightarrow{PD}$$。

题目给出 $$\overrightarrow{PA} = \frac{5}{3}\overrightarrow{PB} - x\overrightarrow{PC} - \frac{1}{3}\overrightarrow{PD}$$，故 $$\frac{5}{3} - x - \frac{1}{3} = 1$$，解得 $$x = \frac{1}{3}$$。

故选 **A**。

3. 解析：

① 正确，若三个向量不能构成基底，则它们线性相关，必共面。

② 正确，若 $$a$$ 和 $$b$$ 不能与任何向量构成基底，说明它们共线。

③ 错误，$$\overrightarrow{OP} = 2\overrightarrow{OA} - 2\overrightarrow{OB} - 2\overrightarrow{OC}$$，系数和为 $$2 - 2 - 2 = -2 \neq 1$$，故 $$P, A, B, C$$ 不共面。

④ 错误，若 $$c$$ 由 $$a$$ 和 $$b$$ 线性表示，则 $$\{a, b, c\}$$ 线性相关，不能构成基底。

⑤ 正确，$$\{a + b, b + c, c + a\}$$ 是线性无关的，可以构成基底。

综上，真命题有 **3** 个，故选 **D**。

4. 解析：

在正方体中，$$\overrightarrow{AC}$$ 是空间对角线，与 $$\overrightarrow{B_1D_1}$$ 平行，故 $$\overrightarrow{B_1D_1}$$ 和 $$\overrightarrow{B_1B}$$ 与 $$\overrightarrow{AC}$$ 共面。

其他选项的向量与 $$\overrightarrow{AC}$$ 不共面。

故选 **A**。

5. 解析：

三点共线，则 $$\overrightarrow{AB}$$ 与 $$\overrightarrow{AC}$$ 共线。计算 $$\overrightarrow{AB} = (1, -1, 3)$$，$$\overrightarrow{AC} = (a - 1, -2, b + 4)$$。

存在实数 $$k$$ 使得 $$\overrightarrow{AC} = k\overrightarrow{AB}$$，即 $$a - 1 = k$$，$$-2 = -k$$，$$b + 4 = 3k$$。

解得 $$k = 2$$，$$a = 3$$，$$b = 2$$。

故选 **A**。

6. 解析：

若 $$l_1 \parallel l_2$$，则方向向量 $$\overrightarrow{a}$$ 和 $$\overrightarrow{b}$$ 成比例，即 $$\frac{4}{3} = \frac{m}{6} = \frac{n}{7}$$。

解得 $$m = 8$$，$$n = \frac{28}{3}$$。

故选 **B**。

7. 解析：

三向量共面，则行列式 $$\begin{vmatrix} 2 & -1 & 3 \\ -1 & 4 & -2 \\ 1 & 3 & \lambda \end{vmatrix} = 0$$。

计算得 $$2(4\lambda + 6) + 1(-\lambda + 2) + 3(-3 - 4) = 0$$，解得 $$\lambda = 1$$。

故选 **A**。

8. 解析：

四点共面的条件是 $$\overrightarrow{OM} = x\overrightarrow{OA} + y\overrightarrow{OB} + z\overrightarrow{OC}$$，且 $$x + y + z = 1$$。

① $$\overrightarrow{MA} = \overrightarrow{MB} + \overrightarrow{MC}$$ 可化为 $$\overrightarrow{OM} = \overrightarrow{OA} - \overrightarrow{OB} - \overrightarrow{OC}$$，系数和为 $$-1 \neq 1$$，不共面。

② $$\overrightarrow{OM} = \overrightarrow{OA} + \overrightarrow{OB} + \overrightarrow{OC}$$，系数和为 $$3 \neq 1$$，不共面。

③ $$\overrightarrow{OM} = 2\overrightarrow{OA} - \overrightarrow{OB} - \overrightarrow{OC}$$，系数和为 $$0 \neq 1$$，不共面。

④ $$\overrightarrow{OM} = \frac{1}{3}\overrightarrow{OA} + \frac{1}{3}\overrightarrow{OB} + \frac{1}{3}\overrightarrow{OC}$$，系数和为 $$1$$，共面。

故选 **D**（①④）。

9. 解析：

$$a = \overrightarrow{OA} + \overrightarrow{OB} + \overrightarrow{OC}$$，$$b = \overrightarrow{OA} + \overrightarrow{OB} - \overrightarrow{OC}$$。

若 $$c$$ 与 $$a, b$$ 不能构成基底，则 $$c$$ 可由 $$a$$ 和 $$b$$ 线性表示。设 $$c = k_1 a + k_2 b$$。

对于 $$\overrightarrow{OC}$$，有 $$\overrightarrow{OC} = \frac{1}{2}(a - b)$$，故 $$\overrightarrow{OC}$$ 不能与 $$a, b$$ 构成基底。

故选 **C**。

10. 解析：

三向量共面，则行列式 $$\begin{vmatrix} 2 & 1 & 3 \\ -1 & 2 & -2 \\ 7 & 6 & \lambda \end{vmatrix} = 0$$。

计算得 $$2(2\lambda + 12) - 1(-\lambda + 14) + 3(-6 - 14) = 0$$，解得 $$\lambda = 10$$。

故选 **A**。

_{题目来源于各渠道收集，若侵权请联系下方邮箱}