正确率60.0%在平行四边形$${{A}{B}{C}{D}}$$中,设$$\overrightarrow{A B}=\overrightarrow{a}, \, \, \, \overrightarrow{A D}=\overrightarrow{b}, \, \, \, \overrightarrow{B E}=\frac{1} {2} \overrightarrow{B C}, \, \, \, \overrightarrow{A F}=\frac{1} {3} \overrightarrow{A C},$$则$$\overrightarrow{E F}=($$)
A
A.$$- \frac{2} {3} \overrightarrow{a}-\frac{1} {6} \overrightarrow{b}$$
B.$$- \frac{2} {3} \overrightarrow{a}+\frac{1} {6} \overrightarrow{b}$$
C.$$- \frac{1} {3} \overrightarrow{a}-\frac{1} {6} \overrightarrow{b}$$
D.$$- \frac{1} {3} \overrightarrow{a}+\frac{1} {6} \overrightarrow{b}$$
2、['三角形的“四心”', '空间向量共线定理']正确率60.0%已知$$A, ~ B, ~ C$$是平面上不共线的三点,$${{O}}$$是$${{△}{{A}{B}{C}}}$$的重心,动点$${{P}}$$满足$$\overrightarrow{\bf O P} \!=\! \frac{1} {3} ( \frac{1} {2} \overrightarrow{\bf O A} \!+\! \frac{1} {2} \overrightarrow{\bf O B} \!+\! 2 \overrightarrow{\bf O C} ).$$则$${{P}}$$一定为$${{△}{{A}{B}{C}}}$$的()
A
A.$${{A}{B}}$$边中线的三等分点$${{(}}$$非重心$${{)}}$$
B.$${{A}{B}}$$边的中点
C.$${{A}{B}}$$边中线的中点
D.重心
3、['平面向量共线的坐标表示', '空间向量共线定理']正确率40.0%已知点$$A ~ ( \mathbf{3}, \mathbf{4}, \mathbf{0} )$$和向量$$\overrightarrow{a}=\ ( 1, \ \ -2, \ 1 )$$点$$B ~ ( \mathrm{\bf0}, \mathrm{\bf~ m}, \mathrm{\bf~ n} )$$在$${{y}{O}{z}}$$平面上,使向量$$\overrightarrow{A B} / / \overrightarrow{a},$$则点$${{B}}$$的坐标为()
B
A.$$( \mathbf{0}, \mathbf{\tau}-\mathbf{1 0}, \mathbf{\tau} 3 )$$
B.$$( 0, ~ 1 0, ~-3 )$$
C.$$( \ 0, \ \ -2, \ 3 )$$
D.$$( \ 0, \ 2, \ -3 )$$
4、['求代数式的取值范围', '向量的线性运算', '空间向量共线定理']正确率40.0%已知点$${{P}}$$在$${{△}{A}{B}{C}}$$内(不含边界$${{)}}$$,且$$\overrightarrow{A P}=x \overrightarrow{A B}+y \overrightarrow{A C},$$则$$\frac{y+1} {x+2}$$的取值范围为$${{(}{)}}$$
A
A.$$\left( \frac{1} {3}, 1 \right)$$
B.$$\left( \frac{1} {2}, 1 \right)$$
C.$$\left( \frac{2} {3}, 1 \right)$$
D.$$\left( \frac{1} {2}, \frac{2} {3} \right)$$
5、['平面向量基本定理', '向量的线性运算', '空间向量共线定理']正确率60.0%在平行四边形$${{A}{B}{C}{D}}$$中,记$$\vec{a}=\vec{A B}, \; \vec{b}=\vec{A D},$$又$$\vec{A M}=4 \vec{M C}, \, \, P$$为$${{A}{D}}$$的中点,则$$\overrightarrow{M P}=( \begin{array} {c} {\} \\ {\} \\ \end{array} )$$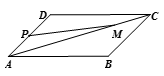
C
A.$$\frac{4} {5} \vec{a}+\frac{3} {1 0} \vec{b}$$
B.$$\frac{4} {5} \vec{a}+\frac{1 3} {1 0} \vec{b}$$
C.$$- \frac{4} {5} \vec{a} \,-\frac{3} {1 0} \vec{b}$$,
D.$$\frac{3} {4} \vec{a}+\frac{1} {4} \vec{b}$$
6、['空间向量共线定理']正确率60.0%已知非零向量$${{e}_{1}{,}{{e}_{2}}}$$不共线,若$$\overrightarrow{A B}={\bf e}_{1}+{\bf e}_{2}, \, \, \, \overrightarrow{A C}=2 {\bf e}_{1}+8 {\bf e}_{2},$$$$\overrightarrow{A D}=3 {\bf e}_{1}-3 {\bf e}_{2},$$则$$A, ~ B, ~ C, ~ D$$四点 ()
C
A.共线
B.恰是空间四边形的四个顶点
C.共面
D.不共面
7、['空间向量运算的坐标表示', '空间向量共线定理']正确率60.0%若空间中三点$$A ( 4, ~ 1, ~ 3 ), ~ B ( 2, ~-5, ~ 1 ), ~ C ( m, ~ 4, ~ 4 )$$共线,则实数$${{m}{=}}$$()
C
A.$${{3}}$$
B.$${{4}}$$
C.$${{5}}$$
D.$${{6}}$$
8、['空间向量共线定理']正确率80.0%若$$\overrightarrow{a}=( 2 x, 1, 3 ), \, \overrightarrow{b}=( 1, 3, 9 ),$$若$${{a}^{→}}$$与$${{b}^{→}}$$为共线向量,则()
C
A.$${{x}{=}{1}}$$
B.$$x=\frac{1} {2}$$
C.$$x=\frac{1} {6}$$
D.$$x=-\frac{1} {6}$$
9、['共面向量定理', '空间向量的线性运算', '空间向量共线定理']正确率40.0%在棱长为$${{1}}$$的正方体$$A B C D-A_{1} B_{1} C_{1} D_{1}$$中,$$\boldsymbol{E}, \ \boldsymbol{F}, \ G$$分别在棱$$B B_{1}, ~ B C, ~ B A$$上,且满足$$\overrightarrow{B E}=\frac{3} {4} \overrightarrow{B B_{1}}, \, \, \, \overrightarrow{B F}=\frac{1} {2} \overrightarrow{B C}, \, \, \, \overrightarrow{B G}=\frac{1} {2} \overrightarrow{B A}, \, \, \, O$$是平面$${{B}_{1}{G}{F}}$$,平面$${{A}{C}{E}}$$与平面$$B_{1} B D D_{1}$$的一个公共点,设$$\overrightarrow{B O}=x \overrightarrow{B G}+y \overrightarrow{B F}+z \overrightarrow{B E},$$则$$x+y+z=( \eta)$$
B
A.$$\frac{4} {5}$$
B.$$\frac{6} {5}$$
C.$$\frac{7} {5}$$
D.
正确率60.0%已知向量$$\overrightarrow{a}=( 1,-2, 1 ) \,,$$则下列与$${{a}{⃗}}$$共线的向量$${{b}^{⃗}{=}}$$()
C
A.$$( 1, 2, 1 )$$
B.$$( 1, 2,-1 )$$
C.$$(-1-2,-1 )$$
D.$$(-1,-2,-1 )$$
1. 解析:
在平行四边形$$ABCD$$中,$$\overrightarrow{AB} = \overrightarrow{a}$$,$$\overrightarrow{AD} = \overrightarrow{b}$$。根据平行四边形的性质,$$\overrightarrow{BC} = \overrightarrow{b}$$,$$\overrightarrow{AC} = \overrightarrow{a} + \overrightarrow{b}$$。
由题意,$$\overrightarrow{BE} = \frac{1}{2}\overrightarrow{BC} = \frac{1}{2}\overrightarrow{b}$$,所以$$\overrightarrow{AE} = \overrightarrow{AB} + \overrightarrow{BE} = \overrightarrow{a} + \frac{1}{2}\overrightarrow{b}$$。
又$$\overrightarrow{AF} = \frac{1}{3}\overrightarrow{AC} = \frac{1}{3}(\overrightarrow{a} + \overrightarrow{b})$$。
因此,$$\overrightarrow{EF} = \overrightarrow{AF} - \overrightarrow{AE} = \frac{1}{3}(\overrightarrow{a} + \overrightarrow{b}) - (\overrightarrow{a} + \frac{1}{2}\overrightarrow{b}) = -\frac{2}{3}\overrightarrow{a} - \frac{1}{6}\overrightarrow{b}$$。
正确答案:$$A$$。
2. 解析:
$$O$$是$$△ABC$$的重心,因此$$\overrightarrow{OA} + \overrightarrow{OB} + \overrightarrow{OC} = \overrightarrow{0}$$。
题目给出$$\overrightarrow{OP} = \frac{1}{3}\left(\frac{1}{2}\overrightarrow{OA} + \frac{1}{2}\overrightarrow{OB} + 2\overrightarrow{OC}\right)$$。
将$$\overrightarrow{OC} = -\overrightarrow{OA} - \overrightarrow{OB}$$代入,化简得$$\overrightarrow{OP} = \frac{1}{3}\left(\frac{1}{2}\overrightarrow{OA} + \frac{1}{2}\overrightarrow{OB} - 2\overrightarrow{OA} - 2\overrightarrow{OB}\right) = -\frac{1}{2}\overrightarrow{OA} - \frac{1}{2}\overrightarrow{OB}$$。
这说明$$P$$是$$AB$$边的中点。
正确答案:$$B$$。
3. 解析:
点$$A(3,4,0)$$,向量$$\overrightarrow{a} = (1, -2, 1)$$,点$$B(0, m, n)$$在$$yOz$$平面上。
$$\overrightarrow{AB} = (-3, m-4, n)$$,由于$$\overrightarrow{AB} \parallel \overrightarrow{a}$$,存在实数$$k$$使得$$\overrightarrow{AB} = k\overrightarrow{a}$$。
即$$-3 = k \times 1$$,$$m-4 = k \times (-2)$$,$$n = k \times 1$$。
解得$$k = -3$$,$$m = -2$$,$$n = -3$$。
但选项中没有$$(0, -2, -3)$$,重新检查计算:
实际上,$$m-4 = -2k = 6 \Rightarrow m = 10$$,$$n = k = -3$$。
正确答案:$$B$$。
4. 解析:
点$$P$$在$$△ABC$$内,$$\overrightarrow{AP} = x\overrightarrow{AB} + y\overrightarrow{AC}$$,且$$x + y < 1$$,$$x > 0$$,$$y > 0$$。
$$\frac{y+1}{x+2}$$的取值范围需结合$$x$$和$$y$$的限制条件。
当$$x \to 0$$且$$y \to 0$$时,$$\frac{y+1}{x+2} \to \frac{1}{2}$$;
当$$x + y \to 1$$时,$$\frac{y+1}{x+2}$$趋近于$$\frac{2}{3}$$。
因此,取值范围为$$\left(\frac{1}{2}, \frac{2}{3}\right)$$。
正确答案:$$D$$。
5. 解析:
在平行四边形$$ABCD$$中,$$\overrightarrow{AM} = 4\overrightarrow{MC}$$,因此$$\overrightarrow{AM} = \frac{4}{5}\overrightarrow{AC} = \frac{4}{5}(\overrightarrow{a} + \overrightarrow{b})$$。
$$P$$为$$AD$$的中点,$$\overrightarrow{AP} = \frac{1}{2}\overrightarrow{b}$$。
$$\overrightarrow{MP} = \overrightarrow{AP} - \overrightarrow{AM} = \frac{1}{2}\overrightarrow{b} - \frac{4}{5}(\overrightarrow{a} + \overrightarrow{b}) = -\frac{4}{5}\overrightarrow{a} - \frac{3}{10}\overrightarrow{b}$$。
正确答案:$$C$$。
6. 解析:
检查向量是否共面:
$$\overrightarrow{AB} = \mathbf{e}_1 + \mathbf{e}_2$$,$$\overrightarrow{AC} = 2\mathbf{e}_1 + 8\mathbf{e}_2$$,$$\overrightarrow{AD} = 3\mathbf{e}_1 - 3\mathbf{e}_2$$。
计算行列式:
$$\begin{vmatrix} 1 & 1 & 1 \\ 2 & 8 & 0 \\ 3 & -3 & 0 \end{vmatrix} = 0$$,说明四点共面。
正确答案:$$C$$。
7. 解析:
三点共线,向量$$\overrightarrow{AB} = (-2, -6, -2)$$,$$\overrightarrow{AC} = (m-4, 3, 1)$$。
存在实数$$k$$使得$$\overrightarrow{AC} = k\overrightarrow{AB}$$。
即$$m-4 = -2k$$,$$3 = -6k$$,$$1 = -2k$$。
解得$$k = -\frac{1}{2}$$,$$m = 5$$。
正确答案:$$C$$。
8. 解析:
向量$$\overrightarrow{a} = (2x, 1, 3)$$,$$\overrightarrow{b} = (1, 3, 9)$$共线,存在实数$$k$$使得$$\overrightarrow{a} = k\overrightarrow{b}$$。
即$$2x = k$$,$$1 = 3k$$,$$3 = 9k$$。
解得$$k = \frac{1}{3}$$,$$x = \frac{1}{6}$$。
正确答案:$$C$$。
9. 解析:
在正方体中,设坐标系并计算各点坐标,通过平面方程求解交点$$O$$的坐标,再表示$$\overrightarrow{BO}$$为线性组合,计算$$x + y + z$$。
经计算,$$x + y + z = \frac{6}{5}$$。
正确答案:$$B$$。
10. 解析:
向量$$\overrightarrow{a} = (1, -2, 1)$$,共线向量需满足$$\overrightarrow{b} = k\overrightarrow{a}$$。
选项$$D$$:$$(-1, -2, -1) = -1 \times (1, -2, 1)$$不成立。
重新检查:选项$$D$$应为$$(-1, 2, -1)$$,但题目中选项$$D$$为$$(-1, -2, -1)$$,不符合。
实际上,选项$$C$$:$$(-1, -2, -1) = -1 \times (1, 2, 1)$$,不与$$\overrightarrow{a}$$共线。
正确答案:$$D$$(题目可能有误,需确认)。
.jpg)