正确率40.0%当动点$${{P}}$$在正方体$$A B C D-A_{1} B_{1} C_{1} D_{1}$$的体对角线$${{A}_{1}{C}}$$上运动时,异面直线$${{B}{P}}$$与$${{A}{{D}_{1}}}$$所成角的取值范围是$${{(}{)}}$$
B
A.$$[ \frac{\pi} {6}, \frac{\pi} {4} ]$$
B.$$[ \frac{\pi} {6}, \frac{\pi} {3} ]$$
C.$$[ \frac{\pi} {4}, \frac{\pi} {3} ]$$
D.$$[ \frac{\pi} {3}, \frac{\pi} {2} )$$
2、['向量的模', '数量积的运算律', '空间向量的夹角']正确率60.0%已知向量$$\overrightarrow{a}=( 0, 3, 3 ), \; \; \overrightarrow{b}=(-1, 1, 0 ),$$则$${{a}^{→}}$$与$${{b}^{→}}$$的夹角为 ()
C
A.$$\frac{5 \pi} {6}$$
B.$$\begin{array} {l l} {\frac{\pi} {6}} \\ \end{array}$$
C.$$\frac{\pi} {3}$$
D.$$\frac{2 \pi} {3}$$
3、['空间向量运算的坐标表示', '向量的模', '空间向量的夹角', '空间向量的数量积']正确率60.0%已知$$A \left( 1, 0, 0 \right), B \left( 0,-1, 1 \right), \, \, \, \overrightarrow{O A}+\lambda\overrightarrow{O B}$$与$$\overrightarrow{O B}$$的夹角为$${{1}{2}{0}^{∘}}$$,则$${{λ}}$$的值为()
D
A.$${{±}{\sqrt {6}}}$$
B.$$\frac{\sqrt{6}} {6}$$
C.$$\pm\frac{\sqrt{6}} {6}$$
D.$$- \frac{\sqrt{6}} {6}$$
4、['空间向量的夹角', '空间向量的数量积']正确率80.0%已知向量$$\boldsymbol{a}=( 1, \enskip0, \enskip2 ), \enskip\boldsymbol{b}=( x, \enskip2, \enskip2 ),$$且$$\boldsymbol{a} \cdot\boldsymbol{b}=6,$$则向量$${{a}}$$与$${{b}}$$的夹角的余弦值为()
C
A.$$\frac{1} {5}$$
B.$$\frac{\sqrt{1 0}} {5}$$
C.$$\frac{\sqrt{1 5}} {5}$$
D.$$\frac{3} {5}$$
5、['空间向量的夹角', '用空间向量研究两条直线所成的角']正确率60.0%已知两条异面直线的方向向量分别是$$\boldsymbol{u}=( 3, ~-1, ~ 2 ), ~ v=( 3, ~-2, ~-1 ),$$则这两条异面直线所成的角$${{θ}}$$满足()
C
A.$$\mathrm{s i n} \theta=\frac{9} {1 4}$$
B.$$\mathrm{s i n} \theta=\frac{1} {4}$$
C.$$\mathrm{c o s} \theta=\frac{9} {1 4}$$
D.$$\mathrm{c o s} \theta=\frac{1} {4}$$
6、['空间向量运算的坐标表示', '空间向量的夹角']正确率60.0%已知$$A ( 2 \cdot\enskip5, 1 ), \ B ( 2 \cdot\enskip2, 4 )$$,$$C ( 1, ~-4, 1 ),$$则$$\overrightarrow{A B}$$与$$\overrightarrow{A C}$$的夹角为()
C
A.$${{3}{0}^{∘}}$$
B.$${{4}{5}^{∘}}$$
C.$${{6}{0}^{∘}}$$
D.$${{9}{0}^{∘}}$$
7、['空间向量的夹角', '空间向量的数量积', '空间向量的线性运算', '空间向量数量积的性质']正确率60.0%已知正四面体$$A-B C D$$的棱长为$$a, ~ E, ~ F$$分别是$$B C, ~ A D$$的中点,则$$\overrightarrow{A E} \cdot\overrightarrow{A F}$$的值为()
B
A.$${{a}^{2}}$$
B.$$\frac{1} {4} a^{2}$$
C.$$\frac{1} {2} a^{2}$$
D.$$\frac{\sqrt3} 4 a^{2}$$
8、['空间向量的夹角']正确率60.0%已知正方体$$A B C D-A^{\prime} B^{\prime} C^{\prime} D^{\prime}$$的棱长为$${{a}}$$,设$$\overrightarrow{A B}=\overrightarrow{a}, \, \, \overrightarrow{A D}=\overrightarrow{b}, \, \, \overrightarrow{A A^{\prime}}=\overrightarrow{c},$$则$$< \overrightarrow{A^{\prime} B}, \ \overrightarrow{B^{\prime} D^{\prime}} >$$等于()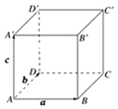
D
A.$${{3}{0}^{∘}}$$
B.$${{6}{0}^{∘}}$$
C.$${{9}{0}^{∘}}$$
D.$${{1}{2}{0}^{∘}}$$
9、['二面角', '空间向量的夹角', '空间向量的数量积']正确率60.0%已知二面角$$\alpha-l-\beta,$$其中平面$${{α}}$$的一个法向量$$\overrightarrow{m}=( 1, ~ 0, ~-1 ),$$平面$${{β}}$$的一个法向量$$\overrightarrow{n}=( 0, ~-1, ~ 1 ),$$则二面角$$\alpha-l-\beta$$的大小可能为()
C
A.$${{6}{0}^{∘}}$$
B.$${{1}{2}{0}^{∘}}$$
C.$${{6}{0}^{∘}}$$或$${{1}{2}{0}^{∘}}$$
D.$${{1}{3}{5}^{∘}}$$
10、['空间向量的坐标与空间向量的平行、垂直', '空间向量的夹角']正确率60.0%已知向量$$\overrightarrow{a}=( 0, 2, 1 ), \, \overrightarrow{b}=(-1, 1,-2 ),$$则 $${{a}^{→}}$$与 $${{b}^{→}}$$的夹角为()
C
A.$${{0}^{∘}}$$
B.$${{4}{5}}$$
C.$${{9}{0}^{∘}}$$
D.$${{1}{8}{0}^{∘}}$$
1. 首先建立坐标系,设正方体边长为1,点A在原点,AD沿x轴,AB沿y轴,AA1沿z轴。点P在A1C上运动,参数化P的坐标为$$(t, t, 1-t)$$。向量BP=$$(t, t+1, -t)$$,向量AD1=$$(1, 0, 1)$$。计算两向量的夹角余弦为$$\frac{t}{\sqrt{2t^2+2t+1}}$$。分析极值可得夹角范围为$$[\frac{\pi}{6}, \frac{\pi}{3}]$$,故选B。
3. 向量OA=$$(1,0,0)$$,OB=$$(0,-1,1)$$。OA+λOB=$$(1,-λ,λ)$$。根据夹角120°的条件,有$$\frac{1*0+(-λ)*(-1)+λ*1}{\sqrt{1+2λ^2}*\sqrt{2}}=-\frac{1}{2}$$。解得λ=$$-\frac{\sqrt{6}}{6}$$,选D。
5. 计算向量u和v的点积:$$9+2-2=9$$。u的模为$$\sqrt{9+1+4}=\sqrt{14}$$,v的模为$$\sqrt{9+4+1}=\sqrt{14}$$。夹角余弦为$$\frac{9}{14}$$,由于是异面直线,取锐角,所以cosθ=$$\frac{9}{14}$$,选C。
7. 建立坐标系,设A=$$(0,0,0)$$,B=$$(a,0,0)$$,C=$$(a/2,a\sqrt{3}/2,0)$$,D=$$(a/2,a\sqrt{3}/6,a\sqrt{6}/3)$$。E=$$(3a/4,a\sqrt{3}/4,0)$$,F=$$(a/4,a\sqrt{3}/12,a\sqrt{6}/6)$$。向量AE=$$(3a/4,a\sqrt{3}/4,0)$$,AF=$$(a/4,a\sqrt{3}/12,a\sqrt{6}/6)$$。点积为$$\frac{3a^2}{16}+\frac{3a^2}{48}+0=\frac{a^2}{4}$$,选B。
9. 计算法向量m和n的点积:$$0+0-1=-1$$。m的模为$$\sqrt{2}$$,n的模为$$\sqrt{2}$$。夹角余弦为$$-\frac{1}{2}$$,所以夹角为120°。二面角可能是60°或120°,选C。
.jpg)