空间向量的线性运算-1.1 空间向量及其运算知识点专题基础单选题自测题答案-湖北省等高一数学选择必修,平均正确率66.0%

正确率60.0%如图，在正方体$$A B C D-A_{1} B_{1} C_{1} D_{1}$$中$${，{E}{，}{F}}$$分别在棱$${{B}{{B}_{1}}}$$和$${{D}{{D}_{1}}}$$上，且$$D F={\frac{1} {2}} D D_{1}$$.记$$\overrightarrow{E F}=x \overrightarrow{A B}+y \overrightarrow{A D}+z \overrightarrow{A A_{1}}，$$若$$x+y+z=\frac1 4，$$则$$\frac{B E} {B B_{1}}=$$（）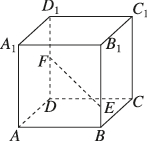

B

A.$$\frac{1} {2}$$

B.$$\frac{1} {4}$$

C.$$\frac{1} {3}$$

D.$$\frac{1} {6}$$

正确率60.0%在正方体$$A B C D-A_{1} B_{1} C_{1} D_{1}$$中，点$${{P}}$$是$${{C}_{1}{{D}_{1}}}$$的中点，且$$\overrightarrow{A P}=\overrightarrow{A D}+x \overrightarrow{A B}+y \overrightarrow{A A_{1}}，$$则实数$${{x}{+}{y}}$$的值为（）

D

A.$$- \frac{3} {2}$$

B.$$- \frac{1} {2}$$

C.$$\frac{1} {2}$$

D.$$\begin{array} {l l} {\frac{3} {2}} \\ \end{array}$$

正确率60.0%三棱柱$$A B C-A_{1} B_{1} C_{1}$$中，$${{N}}$$是$${{A}_{1}{B}}$$的中点，若$$\overrightarrow{C A}=\vec{a}， \， \， \， \overrightarrow{C B}=\vec{b}， \， \， \， \overrightarrow{C C_{1}}=\vec{c}，$$则$$\overrightarrow{C N}=($$）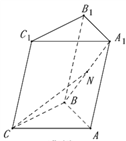

B

A.$$\frac1 2 \left( \vec{a}+\vec{b}-\vec{c} \right)$$

B.$$\frac1 2 \left( \vec{a}+\vec{b}+\vec{c} \right)$$

C.$$\vec{a}+\vec{b}+\frac{1} {2} \vec{c}$$

D.$$\vec{a}+\frac{1} {2} \left( \vec{b}+\vec{c} \right)$$

正确率60.0%在长方体$$A B C D-A_{1} B_{1} C_{1} D_{1}$$中，$$\overrightarrow{A B}=\， \ \overrightarrow{a}， \ \overrightarrow{A D}=\overrightarrow{b}， \ \overrightarrow{A A_{1}}=\overrightarrow{c}， \ E$$是$${{B}{{B}_{1}}}$$中点，则$$\overrightarrow{D_{1} E}=($$）

B

A.$$\overrightarrow{a}+\overrightarrow{b}-2 \overrightarrow{c}$$

B.$$\vec{a}-\vec{b}-\frac{1} {2} \vec{c}$$

C.$$\vec{b}-\vec{a}+\frac{1} {2} \vec{c}$$

D.$$2 \overrightarrow{c}-\overrightarrow{a}-\overrightarrow{b}$$

正确率60.0%直三棱柱$$A B C-A_{1} B_{1} C_{1}$$中，若$$\overrightarrow{C A}=\overrightarrow{a}， \， \， \， \overrightarrow{C B}=\overrightarrow{b}， \， \， \， \overrightarrow{C C_{1}}=\overrightarrow{c}$$，则$$\overrightarrow{A_{1} B}=$$（）

D

A.$$\overrightarrow{a}+\overrightarrow{b}-\overrightarrow{c}$$

B.$$\overrightarrow{a}-\overrightarrow{b}+\overrightarrow{c}$$

C.$$- \overrightarrow{a}+\overrightarrow{b}+\overrightarrow{c}$$

D.$$- \overrightarrow{a}+\overrightarrow{b}-\overrightarrow{c}$$

正确率40.0%在四面体$${{O}{A}{B}{C}}$$中，点$${{M}}$$在$${{O}{A}}$$上，且$$O M=2 M A$$，$${{N}}$$为$${{B}{C}}$$的中点，若$$\overrightarrow{O G}=\frac{1} {3} \overrightarrow{O A}+\frac{x} {4} \overrightarrow{O B}+\frac{x} {4} \overrightarrow{O C}$$，则使$${{G}}$$与$${{M}{、}{N}}$$共线的$${{x}}$$的值为（）

A

A.$${{1}}$$

B.$${{2}}$$

C.$$\begin{array} {l l} {\frac{2} {3}} \\ \end{array}$$

D.$$\frac{4} {3}$$

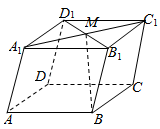
正确率80.0%如图，在平行六面体$$A B C D-A_{1} B_{1} C_{1} D_{1}$$中，$${{M}}$$为$${{A}_{1}{{C}_{1}}}$$与$${{B}_{1}{{D}_{1}}}$$的交点，若$$\overrightarrow{A B}=\overrightarrow{a}， \overrightarrow{A D}=\overrightarrow{b}， \overrightarrow{A A_{1}}=\overrightarrow{c}.$$则下列向量中与$$\overrightarrow{B M}$$相等的向量是$${{(}{)}}$$

A

A.$$- \frac1 2 \overrightarrow{a}+\frac1 2 \overrightarrow{b}+\overrightarrow{c}$$

B.$$\frac{1} {2} \overrightarrow{a}+\frac{1} {2} \overrightarrow{b}+\overrightarrow{c}$$

C.$$- \frac1 2 \overrightarrow{a}-\frac1 2 \overrightarrow{b}+\overrightarrow{c}$$

D.$$\frac{1} {2} \overrightarrow{a}-\frac{1} {2} \overrightarrow{b}+\overrightarrow{c}$$

正确率80.0%已知平行六面体$$A B C D-A^{\prime} B^{\prime} C^{\prime} D^{\prime}$$中，$${{A}{B}{=}{4}}$$，$${{A}{D}{=}{3}}$$，$${{A}{{A}^{′}}{=}{5}}$$， $$\angle B A D=9 0^{\circ}$$， $$\angle B A A^{\prime}=\angle D A A^{\prime}=6 0^{\circ}$$$${{.}}$$则$${{A}{{C}^{′}}}$$的长为$${{(}{)}}$$

A

A.

B.

C.

D.

正确率80.0%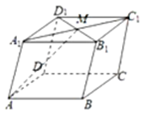如图，在平行六面体$$A B C D-A_{1} B_{1} C_{1} D_{1}$$中，$${{M}}$$为$${{A}_{1}{{C}_{1}}}$$与$${{B}_{1}{{D}_{1}}}$$的交点．若$$\overrightarrow{A B}=\overrightarrow{a}$$，$$\overrightarrow{A D}=\overrightarrow{b}$$，$$\overrightarrow{A A_{1}}=\overrightarrow{c}$$，则下列向量中与$$\overrightarrow{A M}$$相等的向量是$${{(}{)}}$$

B

A.$$- \frac1 2 \overrightarrow{a}+\frac1 2 \overrightarrow{b}+\overrightarrow{c}$$

B.$$\frac{1} {2} \overrightarrow{a}+\frac{1} {2} \overrightarrow{b}+\overrightarrow{c}$$

C.$$- \frac1 2 \overrightarrow{a}-\frac1 2 \overrightarrow{b}+\overrightarrow{c}$$

D.$$\frac{1} {2} \overrightarrow{a}-\frac{1} {2} \overrightarrow{b}+\overrightarrow{c}$$

正确率80.0%如图是元代数学家郭守敬主持建造的观星台，其可近似看作一个正四棱台$$A B C D-A_{1} B_{1} C_{1} D_{1}$$，若$$A B=2 A_{1} B_{1}$$，点$${{M}}$$在$${{B}{{D}_{1}}}$$上，且$$B M=3 D_{1} M$$，则$$\overrightarrow{C M}=( \begin{array} {c} {} \\ {} \\ \end{array} )$$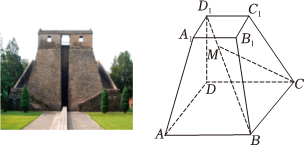

A.$$\frac{3} {4} \overrightarrow{A A_{1}}+\frac{3} {8} \overrightarrow{A B}-\frac{5} {8} \overrightarrow{A D}$$

B.$$\frac{3} {4} \overrightarrow{A A_{1}}+\frac{3} {4} \overrightarrow{A B}-\frac{5} {8} \overrightarrow{A D}$$

C.$${\frac{3} {4}} \overrightarrow{A A_{1}}-{\frac{3} {4}} \overrightarrow{A B}-{\frac{5} {8}} \overrightarrow{A D}$$

D.$${\frac{3} {4}} \overrightarrow{A A_{1}}-{\frac{3} {8}} \overrightarrow{A B}+{\frac{5} {8}} \overrightarrow{A D}$$

1. 设正方体的边长为1，建立坐标系，设点$$A(0,0,0)$$，$$B(1,0,0)$$，$$D(0,1,0)$$，$$A_1(0,0,1)$$。根据题意，$$DF=\frac{1}{2}$$，所以$$F(0,1,\frac{1}{2})$$。设$$\frac{BE}{BB_1}=k$$，则$$E(1,0,k)$$。向量$$\overrightarrow{EF}=(-1,1,\frac{1}{2}-k)$$。又$$\overrightarrow{AB}=(1,0,0)$$，$$\overrightarrow{AD}=(0,1,0)$$，$$\overrightarrow{AA_1}=(0,0,1)$$，所以$$\overrightarrow{EF}=x\overrightarrow{AB}+y\overrightarrow{AD}+z\overrightarrow{AA_1}$$对应分量相等，得$$x=-1$$，$$y=1$$，$$z=\frac{1}{2}-k$$。由$$x+y+z=\frac{1}{4}$$，代入得$$-1+1+\frac{1}{2}-k=\frac{1}{4}$$，解得$$k=\frac{1}{4}$$。故选B。

2. 设正方体的边长为1，建立坐标系，设点$$A(0,0,0)$$，$$D(0,1,0)$$，$$B(1,0,0)$$，$$A_1(0,0,1)$$。点$$P$$为$$C_1D_1$$的中点，所以$$P(\frac{1}{2},1,1)$$。向量$$\overrightarrow{AP}=(\frac{1}{2},1,1)$$。又$$\overrightarrow{AD}=(0,1,0)$$，$$\overrightarrow{AB}=(1,0,0)$$，$$\overrightarrow{AA_1}=(0,0,1)$$，所以$$\overrightarrow{AP}=\overrightarrow{AD}+x\overrightarrow{AB}+y\overrightarrow{AA_1}$$对应分量相等，得$$x=\frac{1}{2}$$，$$y=1$$。故$$x+y=\frac{3}{2}$$。选D。

3. 点$$N$$是$$A_1B$$的中点，所以$$\overrightarrow{CN}=\frac{1}{2}(\overrightarrow{CA_1}+\overrightarrow{CB})$$。又$$\overrightarrow{CA_1}=\overrightarrow{CA}+\overrightarrow{AA_1}=\vec{a}+\vec{c}$$，所以$$\overrightarrow{CN}=\frac{1}{2}(\vec{a}+\vec{c}+\vec{b})=\frac{1}{2}(\vec{a}+\vec{b}+\vec{c})$$。故选B。

4. 设点$$D_1(0,1,1)$$，$$E(1,0,\frac{1}{2})$$。向量$$\overrightarrow{D_1E}=(1,-1,-\frac{1}{2})$$。又$$\overrightarrow{a}=(1,0,0)$$，$$\overrightarrow{b}=(0,1,0)$$，$$\overrightarrow{c}=(0,0,1)$$，所以$$\overrightarrow{D_1E}=\overrightarrow{a}-\overrightarrow{b}-\frac{1}{2}\overrightarrow{c}$$。故选B。

5. 向量$$\overrightarrow{A_1B}=\overrightarrow{CB}-\overrightarrow{CA_1}=\vec{b}-(\vec{a}+\vec{c})=-\vec{a}+\vec{b}-\vec{c}$$。故选D。

6. 点$$M$$在$$OA$$上且$$OM=2MA$$，所以$$\overrightarrow{OM}=\frac{2}{3}\overrightarrow{OA}$$。点$$N$$为$$BC$$的中点，所以$$\overrightarrow{ON}=\frac{1}{2}(\overrightarrow{OB}+\overrightarrow{OC})$$。要使$$G$$与$$M$$、$$N$$共线，需$$\overrightarrow{OG}$$是$$\overrightarrow{OM}$$和$$\overrightarrow{ON}$$的线性组合。由$$\overrightarrow{OG}=\frac{1}{3}\overrightarrow{OA}+\frac{x}{4}\overrightarrow{OB}+\frac{x}{4}\overrightarrow{OC}$$，令$$\overrightarrow{OG}=k\overrightarrow{OM}+(1-k)\overrightarrow{ON}$$，解得$$x=\frac{4}{3}$$。故选D。

7. 点$$M$$为$$A_1C_1$$与$$B_1D_1$$的交点，即$$A_1C_1$$的中点。所以$$\overrightarrow{BM}=\overrightarrow{BA}+\overrightarrow{AM}=-\overrightarrow{a}+\frac{1}{2}(\overrightarrow{A_1}+\overrightarrow{C_1})=-\overrightarrow{a}+\frac{1}{2}(\overrightarrow{b}+\overrightarrow{c})$$。故选A。

8. 向量$$\overrightarrow{AC'}=\overrightarrow{AB}+\overrightarrow{AD}+\overrightarrow{AA'}$$。计算其模长：$$|\overrightarrow{AC'}|^2=|\overrightarrow{AB}|^2+|\overrightarrow{AD}|^2+|\overrightarrow{AA'}|^2+2\overrightarrow{AB}\cdot\overrightarrow{AD}+2\overrightarrow{AB}\cdot\overrightarrow{AA'}+2\overrightarrow{AD}\cdot\overrightarrow{AA'}$$。代入已知条件得$$|\overrightarrow{AC'}|^2=16+9+25+0+20+15=85$$，所以$$|\overrightarrow{AC'}|=\sqrt{85}$$。选D。

9. 点$$M$$为$$A_1C_1$$与$$B_1D_1$$的交点，即$$A_1C_1$$的中点。所以$$\overrightarrow{AM}=\overrightarrow{AA_1}+\overrightarrow{A_1M}=\overrightarrow{c}+\frac{1}{2}(\overrightarrow{A_1B_1}+\overrightarrow{A_1D_1})=\overrightarrow{c}+\frac{1}{2}(\overrightarrow{a}+\overrightarrow{b})$$。故选B。

10. 设$$A_1B_1=1$$，则$$AB=2$$。建立坐标系，设$$A(0,0,0)$$，$$B(2,0,0)$$，$$D(0,2,0)$$，$$A_1(0,0,h)$$。点$$M$$在$$BD_1$$上且$$BM=3D_1M$$，所以$$\overrightarrow{BM}=\frac{3}{4}\overrightarrow{BD_1}$$。计算$$\overrightarrow{BD_1}=(-2,2,h)$$，所以$$\overrightarrow{BM}=\frac{3}{4}(-2,2,h)=(-\frac{3}{2},\frac{3}{2},\frac{3h}{4})$$。点$$C(2,2,0)$$，所以$$\overrightarrow{CM}=\overrightarrow{BM}-\overrightarrow{BC}=(-\frac{3}{2},\frac{3}{2},\frac{3h}{4})-(0,2,0)=(-\frac{3}{2},-\frac{1}{2},\frac{3h}{4})$$。又$$\overrightarrow{AA_1}=(0,0,h)$$，$$\overrightarrow{AB}=(2,0,0)$$，$$\overrightarrow{AD}=(0,2,0)$$，所以$$\overrightarrow{CM}=\frac{3h}{4h}\overrightarrow{AA_1}-\frac{3}{4}\overrightarrow{AB}-\frac{5}{8}\overrightarrow{AD}$$。化简得$$\overrightarrow{CM}=\frac{3}{4}\overrightarrow{AA_1}-\frac{3}{4}\overrightarrow{AB}-\frac{5}{8}\overrightarrow{AD}$$。故选C。