正确率80.0%已知向量$$\boldsymbol{a}=( 3, \textit{}-2, \textbf{} 1 ), \emph{b}=\left(-1, \textit{} \frac{2} {3}, \textbf{} m \right),$$若$$\mathbf{a} / / \mathbf{b},$$则实数$${{m}}$$的值为()
D
A.$${{3}}$$
B.$${{−}{3}}$$
C.$$\frac{1} {3}$$
D.$$- \frac{1} {3}$$
2、['空间向量的坐标与空间向量的平行、垂直']正确率60.0%已知直线$${{l}}$$的一个方向向量为$$\boldsymbol{m}=( 2, ~-1, ~ 3 ),$$且直线$${{l}}$$过$$A ( 0, ~ y, ~ 3 )$$和$$B (-1, ~ 2, ~ z )$$两点,则$${{y}{−}{z}{=}}$$()
A
A.$${{0}}$$
B.$${{2}}$$
C.$$\frac{1} {2}$$
D.$${{3}}$$
3、['空间向量的坐标与空间向量的平行、垂直', '空间直角坐标系中两点之间的距离公式', '空间向量的数量积', '立体几何中的轨迹问题']正确率40.0%如图,在棱长为$${{2}}$$的正方体$$A B C D-A_{1} B_{1} C_{1} D_{1}$$中$${,{E}}$$为$${{B}{C}}$$的中点,点$${{P}}$$在底面$${{A}{B}{C}{D}}$$上(包括边界)移动,且满足$$B_{1} P \perp D_{1} E,$$则$${{B}_{1}{P}}$$的长度的最大值为()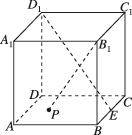
D
A.$$\frac{6 \sqrt{5}} {5}$$
B.$${{2}{\sqrt {5}}}$$
C.$${{2}{\sqrt {2}}}$$
D.$${{3}}$$
4、['空间向量的坐标与空间向量的平行、垂直', '空间中平面与平面的位置关系', '平面的法向量及其应用', '用空间向量研究空间中直线、平面的平行', '空间向量共线定理']正确率80.0%两个不重合平面的法向量分别为$$\boldsymbol{v}_{1}=( 1, ~ 0, ~-1 ), ~ \boldsymbol{v}_{2}=(-2, ~ 0, ~ 2 ),$$则这两个平面的位置关系是()
A
A.平行
B.相交不垂直
C.垂直
D.以上都不对
5、['空间向量的坐标与空间向量的平行、垂直']正确率60.0%已知两个向量$$\overrightarrow{a}=( 2,-1, 3 )$$,$$\overrightarrow{b}=( 4, m, n )$$,且$$\overrightarrow{a} / / \overrightarrow{b}$$,则$${{m}{+}{n}}$$的值为()
C
A.$${{1}}$$
B.$${{2}}$$
C.$${{4}}$$
D.$${{8}}$$
6、['空间向量的坐标与空间向量的平行、垂直', '空间向量运算的坐标表示', '用空间向量研究点到直线的距离']正确率60.0%$${{△}{A}{B}{C}}$$的三个顶点分别是$$A ( 1, ~-1, ~ 2 ), ~ B ( 5, ~-6, ~ 2 )$$,$$C ( 1, ~ 3, ~-1 ),$$则$${{A}{C}}$$边上的高$${{B}{D}}$$长为()
A
A.$${{5}}$$
B.$${\sqrt {{4}{1}}}$$
C.$${{4}}$$
D.$${{2}{\sqrt {5}}}$$
7、['空间向量的坐标与空间向量的平行、垂直']正确率60.0%已知向量$$\overrightarrow{a}=( 2, \; \;-3, \; 1 ), \; \; \overrightarrow{b}=(-4, \; \; 2, \; \; x ),$$且$$\overrightarrow{a} \perp\overrightarrow{b},$$则$${{x}}$$的值为()
D
A.$${{1}{2}}$$
B.$${{1}{0}}$$
C.$${{−}{{1}{4}}}$$
D.$${{1}{4}}$$
8、['空间向量的坐标与空间向量的平行、垂直', '平面的法向量及其应用']正确率60.0%若$$A ( 0, 2, \frac{1 9} {8} ), \, \, \, B ( 1,-1, \frac{5} {8} ), \, \, \, C (-2, 1, \frac{5} {8} )$$是平面$${{α}}$$内的三点,设平面$${{α}}$$的法向量$$\overrightarrow{a}=( x, y, z ),$$则$$x \colon~ y \colon~ z=( ~ ~ )$$
A
A.$$2. ~ 3 : ~ (-4 )$$
B.$$1 : ~ 1 : ~ 1$$
C.$$- \frac{1} {2}, ~ 1. ~ 1$$
D.
正确率60.0%已知向量$$\overrightarrow{a}=\ ( 1, \ 2, \ -2 ) \, \ \overrightarrow{b}=\ ( \ -3, \ -6, \ 6 ) \, \ \overrightarrow{c}=\ ( \ 2, \ 1, \ 2 )$$则它们的位置关系是()
D
A.$$\overrightarrow{a} / / \overrightarrow{b}, \, \, \overrightarrow{a} / / \overrightarrow{c}$$
B.$$\overrightarrow{a} \perp\overrightarrow{b}, \ \overrightarrow{a} \perp\overrightarrow{c}$$
C.$$\overrightarrow{a} \perp\stackrel{\rightarrow} {b}, \ \overrightarrow{b} / \! / \overrightarrow{c}$$
D.$$\overrightarrow{a} / / \overrightarrow{b}, \overrightarrow{b} \perp\overrightarrow{c}$$
10、['空间向量的坐标与空间向量的平行、垂直', '空间向量共线定理']正确率60.0%已知向量$$\overrightarrow{a}=( 2,-3, 5 )$$与向量$$\overrightarrow{b}=(-4, x, y )$$平行,则$${{x}{,}{y}}$$的值分别是$${{(}{)}}$$
D
A.$${{6}}$$和$${{1}{0}}$$
B.$${{−}{6}}$$和$${{1}{0}}$$
C.$${{−}{6}}$$和$${{−}{{1}{0}}}$$
D.$${{6}}$$和$${{−}{{1}{0}}}$$
1. 由于向量 $$\boldsymbol{a}$$ 和 $$\boldsymbol{b}$$ 平行,存在实数 $$k$$ 使得 $$\boldsymbol{b} = k \boldsymbol{a}$$。因此:
故选 D。
2. 直线方向向量 $$\boldsymbol{m}$$ 与 $$\overrightarrow{AB}$$ 平行,$$\overrightarrow{AB} = (-1, 2-y, z-3)$$。因此:
故选 A。
3. 建立坐标系,设 $$P(x, y, 0)$$,$$B_1(2, 0, 2)$$,$$D_1(0, 2, 2)$$,$$E(2, 1, 0)$$。向量 $$\overrightarrow{B_1P} = (x-2, y, -2)$$,$$\overrightarrow{D_1E} = (2, -1, -2)$$。由垂直条件:
故选 C。
4. 法向量 $$\boldsymbol{v}_2 = -2\boldsymbol{v}_1$$,故两平面平行。
故选 A。
5. 由 $$\overrightarrow{a} \parallel \overrightarrow{b}$$,存在 $$k$$ 使得 $$\overrightarrow{b} = k\overrightarrow{a}$$,则:
故选 C。
6. 向量 $$\overrightarrow{AC} = (0, 4, -3)$$,$$\overrightarrow{AB} = (4, -5, 0)$$。高 $$BD$$ 长度为:
故选 C。
7. 由垂直条件:
故选 D。
8. 向量 $$\overrightarrow{AB} = (1, -3, -\frac{7}{4})$$,$$\overrightarrow{AC} = (-2, -1, -\frac{7}{4})$$。法向量满足:
故选 A。
9. 观察向量:
故选 D。
10. 由平行条件:
故选 D。
题目来源于各渠道收集,若侵权请联系下方邮箱.jpg)