1、['空间向量运算的坐标表示', '向量的模', '空间向量的数量积', '空间向量数量积的性质']正确率60.0%已知$$\overrightarrow{a}=( 1, 2, 3 ),$$$$\overrightarrow{b}=( 3, 0,-1 ),$$$$\overrightarrow{c}=\left(-\frac{1} {5}, 1,-\frac{3} {5} \right)$$给出下列等式:
①$$| \overrightarrow{a}+\overrightarrow{b}+\overrightarrow{c} |=| \overrightarrow{a}-\overrightarrow{b}-\overrightarrow{c} |$$;
②$$( \overrightarrow{a}+\overrightarrow{b} ) \cdot\overrightarrow{c}=\overrightarrow{a} \cdot( \overrightarrow{b}+\overrightarrow{c} )$$;
③$$( \overrightarrow{a}+\overrightarrow{b}+\overrightarrow{c} )^{2}=\overrightarrow{a}^{2}+\overrightarrow{b}^{2}+\overrightarrow{c}^{2}$$
④$$( \overrightarrow{a} \cdot\overrightarrow{b} ) \cdot\overrightarrow{c}=\overrightarrow{a} \cdot( \overrightarrow{b} \cdot\overrightarrow{c} )$$.
其中正确的个数是()
D
A.$${{1}}$$个
B.$${{2}}$$个
C.$${{3}}$$个
D.$${{4}}$$个
2、['空间向量运算的坐标表示']正确率80.0%在空间直角坐标系中,点$$P ( 1, ~ 2, ~-3 )$$关于$${{x}{O}{y}}$$平面的对称点为()
D
A.$$(-1, ~-2, ~ 3 )$$
B.$$(-1, ~-2, ~-3 )$$
C.$$(-1, ~ 2, ~-3 )$$
D.$$( 1, ~ 2, ~ 3 )$$
3、['空间向量运算的坐标表示', '空间向量的数量积']正确率60.0%在空间直角坐标系$${{O}{x}{y}{z}}$$中,$$O ( 0, ~ 0, ~ 0 )$$,$$E ( 2 \sqrt{2}, ~ 0, ~ 0 )$$,$$F ( 0, ~ 2 \sqrt{2}, ~ 0 )$$,$${{B}}$$为$${{E}{F}}$$的中点$${,{C}}$$为空间一点且满足$$| \overrightarrow{C O} |=| \overrightarrow{C B} |=3.$$若$$\operatorname{c o s} \langle\overrightarrow{E F}, \ \overrightarrow{B C} \rangle=\frac{1} {6},$$则$$\overrightarrow{O C} \cdot\overrightarrow{O F}=$$()
D
A.$${{9}}$$
B.$${{7}}$$
C.$${{5}}$$
D.$${{3}}$$
4、['空间向量运算的坐标表示', '空间直角坐标系中中点坐标公式']正确率80.0%在空间直角坐标系中,已知点 $$A ( 3, ~ 0, ~ 4 )$$ , $$B (-1, ~ 4, ~ 2 )$$ ,则线段$${{A}{B}}$$的中点坐标与向量 $$\overrightarrow{A B}$$的模分别是()
B
A.$$( 1, ~ 2, ~ 3 ), ~ 5$$
B.$$( 1, ~ 2, ~ 3 ), ~ 6$$
C.$$(-2, ~ 2, ~-1 ), ~ 5$$
D.$$(-2, ~ 2, ~-1 ), ~ 6$$
5、['空间直角坐标系', '空间向量运算的坐标表示']正确率80.0%在空间直角坐标系中,点$$P ( 1, 4,-3 )$$与点$$Q ( 3,-2, 5 )$$关于点$${{M}}$$对称,则点$${{M}}$$的坐标为$${{(}{)}}$$
A.$$( 4, 2, 2 )$$
B.$$( 2,-1, 2 )$$
C.$$( 2, 1, 1 )$$
D.$$( 4,-1, 2 )$$
6、['空间向量运算的坐标表示', '空间向量共线定理']正确率60.0%已知$$A ~ ( \mathrm{\vspace{b o l d} ~ 3, \hspace{b o l d} ~ 4, \hspace{b o l d} ~ 5 ~} ) ~ ~,$$$$B ~ ( \ 0, \ 2, \ 1 ) ~,$$$$O ~ ( \mathbf{0}, \mathbf{0}, \mathbf{0} )$$,若$$\overrightarrow{O C}=\frac{2} {5} \overrightarrow{A B}$$,则点$${{C}}$$的坐标是()
A
A.$$( \mathrm{~}-\frac{6} {5},-\frac{4} {5},-\frac{8} {5} )$$
B.$$( \frac{6} {5},-\frac{4} {5},-\frac{8} {5} )$$
C.$$( \mathrm{~-~} \frac{6} {5},-\frac{4} {5}, \frac{8} {5} )$$
D.$$( \frac{6} {5}, \frac{4} {5}, \frac{8} {5} )$$
7、['空间向量运算的坐标表示']正确率80.0%已知点$$B ~ ( \mathrm{\bf~ 2}, \mathrm{\bf~-3}, \mathrm{\bf~ 1} )$$,向量$$\overrightarrow{A B}=(-3, 5, \ 2 )$$,则点$${{A}}$$坐标是()
D
A.$$( 1, ~ 2, ~ 3 )$$
B.$$( \ -1, \ 2, \ 3 )$$
C.$$( \mathbf{\theta}-5, \mathbf{\ 8}, \mathbf{\ 1} )$$
D.$$( \mathbf{5}, \mathbf{\tau}-\mathbf{8}, \mathbf{\tau}-1 )$$
8、['空间向量运算的坐标表示', '空间直角坐标系中两点之间的距离公式', '空间向量数量积的性质']正确率60.0%已知空间三点$$A ( 0, 2, 3 ), B (-2, 1, 6 ), C ( 1,-1, 5 )$$,则以$$A B, \, A C$$为邻边的平行四边形的面积为()
C
A.$$\frac{7 \sqrt{3}} {2}$$
B.$${{7}}$$
C.$${{7}{\sqrt {3}}}$$
D.$${{1}{4}}$$
9、['空间向量运算的坐标表示', '共面向量定理']正确率60.0%若$$\overrightarrow{a}=\left( 1, \lambda, 2 \right), \overrightarrow{b}=\left( 2,-1, 2 \right), \overrightarrow{c}=\left( 1, 4, 4 \right)$$,且$${{a}^{→}{,}{{b}^{→}}}$$共面,则$${{λ}{=}}$$()
A
A.$${{1}}$$
B.$${{−}{1}}$$
C.$${{1}}$$或$${{2}}$$
D.$${{±}{1}}$$
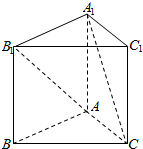
10、['空间直角坐标系', '空间向量运算的坐标表示', '用空间向量研究两条直线所成的角']正确率60.0%如图,已知正三棱柱$$A B C \!-\! A_{1} B_{1} C_{1}$$的各条棱长都相等,则异面直线$${{A}{{B}_{1}}}$$和$${{A}_{1}{C}}$$所成的角的余弦值大小为()
A
A.$$\frac{1} {4}$$
B.$$- \frac{1} {4}$$
C.$$\frac{1} {2}$$
D.$$- \frac{1} {2}$$
1. 解析:
首先计算各个向量的和与差:
$$ \overrightarrow{a} + \overrightarrow{b} + \overrightarrow{c} = (1+3-\frac{1}{5}, 2+0+1, 3-1-\frac{3}{5}) = \left(\frac{19}{5}, 3, \frac{7}{5}\right) $$
$$ \overrightarrow{a} - \overrightarrow{b} - \overrightarrow{c} = (1-3+\frac{1}{5}, 2-0-1, 3+1+\frac{3}{5}) = \left(-\frac{9}{5}, 1, \frac{23}{5}\right) $$
验证等式①:
$$ | \overrightarrow{a} + \overrightarrow{b} + \overrightarrow{c} | = \sqrt{\left(\frac{19}{5}\right)^2 + 3^2 + \left(\frac{7}{5}\right)^2} = \sqrt{\frac{361}{25} + 9 + \frac{49}{25}} = \sqrt{\frac{410}{25} + 9} = \sqrt{\frac{655}{25}} $$
$$ | \overrightarrow{a} - \overrightarrow{b} - \overrightarrow{c} | = \sqrt{\left(-\frac{9}{5}\right)^2 + 1^2 + \left(\frac{23}{5}\right)^2} = \sqrt{\frac{81}{25} + 1 + \frac{529}{25}} = \sqrt{\frac{610}{25} + 1} = \sqrt{\frac{635}{25}} $$
显然不相等,①错误。
验证等式②:
$$ (\overrightarrow{a} + \overrightarrow{b}) \cdot \overrightarrow{c} = (4, 2, 2) \cdot \left(-\frac{1}{5}, 1, -\frac{3}{5}\right) = 4 \times -\frac{1}{5} + 2 \times 1 + 2 \times -\frac{3}{5} = -\frac{4}{5} + 2 - \frac{6}{5} = 0 $$
$$ \overrightarrow{a} \cdot (\overrightarrow{b} + \overrightarrow{c}) = (1, 2, 3) \cdot \left(\frac{14}{5}, -1, -\frac{8}{5}\right) = 1 \times \frac{14}{5} + 2 \times -1 + 3 \times -\frac{8}{5} = \frac{14}{5} - 2 - \frac{24}{5} = -\frac{10}{5} - 2 = -4 $$
不相等,②错误。
验证等式③:
$$ (\overrightarrow{a} + \overrightarrow{b} + \overrightarrow{c})^2 = \left(\frac{19}{5}\right)^2 + 3^2 + \left(\frac{7}{5}\right)^2 = \frac{361}{25} + 9 + \frac{49}{25} = \frac{410}{25} + 9 = \frac{655}{25} $$
$$ \overrightarrow{a}^2 + \overrightarrow{b}^2 + \overrightarrow{c}^2 = 1^2 + 2^2 + 3^2 + 3^2 + 0^2 + (-1)^2 + \left(-\frac{1}{5}\right)^2 + 1^2 + \left(-\frac{3}{5}\right)^2 = 1 + 4 + 9 + 9 + 0 + 1 + \frac{1}{25} + 1 + \frac{9}{25} = 25 + \frac{10}{25} = \frac{635}{25} $$
不相等,③错误。
验证等式④:
$$ \overrightarrow{a} \cdot \overrightarrow{b} = 1 \times 3 + 2 \times 0 + 3 \times (-1) = 0 $$
$$ (\overrightarrow{a} \cdot \overrightarrow{b}) \cdot \overrightarrow{c} = 0 \cdot \overrightarrow{c} = \overrightarrow{0} $$
$$ \overrightarrow{b} \cdot \overrightarrow{c} = 3 \times -\frac{1}{5} + 0 \times 1 + (-1) \times -\frac{3}{5} = -\frac{3}{5} + 0 + \frac{3}{5} = 0 $$
$$ \overrightarrow{a} \cdot (\overrightarrow{b} \cdot \overrightarrow{c}) = \overrightarrow{a} \cdot 0 = \overrightarrow{0} $$
等式成立,④正确。
综上,只有④正确,答案为 $$A$$。
2. 解析:
点 $$P(1, 2, -3)$$ 关于 $$xOy$$ 平面的对称点,$$z$$ 坐标取反,坐标为 $$(1, 2, 3)$$,答案为 $$D$$。
3. 解析:
首先确定点 $$B$$ 为 $$EF$$ 的中点:
$$ B = \left(\frac{2\sqrt{2} + 0}{2}, \frac{0 + 2\sqrt{2}}{2}, \frac{0 + 0}{2}\right) = (\sqrt{2}, \sqrt{2}, 0) $$
设点 $$C = (x, y, z)$$,由 $$| \overrightarrow{CO} | = | \overrightarrow{CB} | = 3$$ 得:
$$ \sqrt{x^2 + y^2 + z^2} = 3 $$
$$ \sqrt{(x - \sqrt{2})^2 + (y - \sqrt{2})^2 + z^2} = 3 $$
平方后相减得:
$$ -2\sqrt{2}x - 2\sqrt{2}y + 4 = 0 \Rightarrow x + y = \sqrt{2} $$
向量 $$\overrightarrow{EF} = (-2\sqrt{2}, 2\sqrt{2}, 0)$$,$$\overrightarrow{BC} = (x - \sqrt{2}, y - \sqrt{2}, z)$$。
由 $$\cos \langle \overrightarrow{EF}, \overrightarrow{BC} \rangle = \frac{1}{6}$$ 得:
$$ \frac{(-2\sqrt{2})(x - \sqrt{2}) + (2\sqrt{2})(y - \sqrt{2})}{\sqrt{(-2\sqrt{2})^2 + (2\sqrt{2})^2} \cdot \sqrt{(x - \sqrt{2})^2 + (y - \sqrt{2})^2 + z^2}} = \frac{1}{6} $$
化简得:
$$ \frac{-2\sqrt{2}x + 4 + 2\sqrt{2}y - 4}{4 \times 3} = \frac{1}{6} \Rightarrow \frac{-2\sqrt{2}x + 2\sqrt{2}y}{12} = \frac{1}{6} \Rightarrow -x + y = \frac{\sqrt{2}}{2} $$
结合 $$x + y = \sqrt{2}$$,解得 $$x = \frac{\sqrt{2}}{4}$$,$$y = \frac{3\sqrt{2}}{4}$$。
代入 $$x^2 + y^2 + z^2 = 9$$ 得:
$$ \frac{2}{16} + \frac{18}{16} + z^2 = 9 \Rightarrow \frac{20}{16} + z^2 = 9 \Rightarrow z^2 = \frac{124}{16} \Rightarrow z = \pm \frac{\sqrt{31}}{2} $$
计算 $$\overrightarrow{OC} \cdot \overrightarrow{OF} = x \times 0 + y \times 2\sqrt{2} + z \times 0 = \frac{3\sqrt{2}}{4} \times 2\sqrt{2} = 3$$,答案为 $$D$$。
4. 解析:
中点坐标为:
$$ \left(\frac{3 + (-1)}{2}, \frac{0 + 4}{2}, \frac{4 + 2}{2}\right) = (1, 2, 3) $$
向量 $$\overrightarrow{AB} = (-1 - 3, 4 - 0, 2 - 4) = (-4, 4, -2)$$,模为:
$$ \sqrt{(-4)^2 + 4^2 + (-2)^2} = \sqrt{16 + 16 + 4} = 6 $$
答案为 $$B$$。
5. 解析:
中点 $$M$$ 的坐标为:
$$ \left(\frac{1 + 3}{2}, \frac{4 + (-2)}{2}, \frac{-3 + 5}{2}\right) = (2, 1, 1) $$
答案为 $$C$$。
6. 解析:
向量 $$\overrightarrow{AB} = (0 - 3, 2 - 4, 1 - 5) = (-3, -2, -4)$$,
$$\overrightarrow{OC} = \frac{2}{5} \overrightarrow{AB} = \left(\frac{2}{5} \times -3, \frac{2}{5} \times -2, \frac{2}{5} \times -4\right) = \left(-\frac{6}{5}, -\frac{4}{5}, -\frac{8}{5}\right)$$,
点 $$C$$ 的坐标为 $$\left(-\frac{6}{5}, -\frac{4}{5}, -\frac{8}{5}\right)$$,答案为 $$A$$。
7. 解析:
设点 $$A = (x, y, z)$$,则 $$\overrightarrow{AB} = (2 - x, -3 - y, 1 - z) = (-3, 5, 2)$$,
解得 $$x = 5$$,$$y = -8$$,$$z = -1$$,即 $$A(5, -8, -1)$$,答案为 $$D$$。
8. 解析:
向量 $$\overrightarrow{AB} = (-2 - 0, 1 - 2, 6 - 3) = (-2, -1, 3)$$,
$$\overrightarrow{AC} = (1 - 0, -1 - 2, 5 - 3) = (1, -3, 2)$$,
叉积 $$\overrightarrow{AB} \times \overrightarrow{AC} = (-1 \times 2 - 3 \times (-3), 3 \times 1 - (-2) \times 2, -2 \times (-3) - (-1) \times 1) = (7, 7, 7)$$,
模为 $$\sqrt{7^2 + 7^2 + 7^2} = 7\sqrt{3}$$,面积为 $$7\sqrt{3}$$,答案为 $$C$$。
9. 解析:
共面条件为行列式为零:
$$ \begin{vmatrix} 1 & \lambda & 2 \\ 2 & -1 & 2 \\ 1 & 4 & 4 \end{vmatrix} = 1 \times (-1 \times 4 - 2 \times 4) - \lambda \times (2 \times 4 - 2 \times 1) + 2 \times (2 \times 4 - (-1) \times 1) = -12 - 6\lambda + 18 = 0 $$
解得 $$\lambda = 1$$,答案为 $$A$$。
10. 解析:
设棱长为 1,建立坐标系,设 $$A(0, 0, 0)$$,$$B(1, 0, 0)$$,$$C\left(\frac{1}{2}, \frac{\sqrt{3}}{2}, 0\right)$$,$$A_1(0, 0, 1)$$,$$B_1(1, 0, 1)$$,$$C_1\left(\frac{1}{2}, \frac{\sqrt{3}}{2}, 1\right)$$。
向量 $$\overrightarrow{AB_1} = (1, 0, 1)$$,$$\overrightarrow{A_1C} = \left(\frac{1}{2}, \frac{\sqrt{3}}{2}, -1\right)$$,
点积为 $$1 \times \frac{1}{2} + 0 \times \frac{\sqrt{3}}{2} + 1 \times (-1) = -\frac{1}{2}$$,
模分别为 $$\sqrt{1 + 0 + 1} = \sqrt{2}$$ 和 $$\sqrt{\frac{1}{4} + \frac{3}{4} + 1} = \sqrt{2}$$,
余弦值为 $$\frac{-\frac{1}{2}}{2} = -\frac{1}{4}$$,答案为 $$B$$。
题目来源于各渠道收集,若侵权请联系下方邮箱

.jpg)