正确率60.0%在空间直角坐标系$$O-x y z$$中,给出以下结论:$${①}$$点$$A ( 1, ~-3, ~ 4 )$$关于原点的对称点的坐标为$$( \mathbf{\alpha}-1, \mathbf{\alpha}-3, \mathbf{\alpha}-4 ) \mathbf{\alpha}, \mathbf{\alpha}$$点$$P ~ ( ~-1, ~ 2, ~ 3 )$$关于$${{x}{O}{z}}$$平面对称的点的坐标是$$( \mathbf{\alpha}-\mathbf{1}, \mathbf{\alpha}-\mathbf{2}, \mathbf{3} ) \mathbf{\alpha}, \mathbf{\beta}$$已知点$$A ~ ( ~-3, ~ 1, ~ 5 )$$与点$$B ~ ( \mathrm{~ 4, ~ 3, ~ 1 ~} )$$,则$${{A}{B}}$$的中点坐标是$$( \mathrm{\bf~ \frac{1} {2}, \mathrm{\bf~ 2}, \mathrm{\bf~ 3} ) ~}, \mathrm{\bf~ \frac{1} {4} ~}$$两点$$M ~ ( \mathrm{~-~ 1, ~ 1, ~ 2 ) ~, ~} ~ N ~ ( \mathrm{~ 1, ~ 3 ~} )$$间的距离为$${{5}}$$.其中正确的是()
C
A.$${①{②}}$$
B.$${①{③}}$$
C.$${②{③}}$$
D.$${②{④}}$$
2、['空间直角坐标系中两点之间的距离公式', '二次函数的图象分析与判断']正确率60.0%已知$$A ( x, 5-x, 2 x-1 )$$,$$B ( 1, x+2, 2-x )$$,当$${{|}{A}{B}{|}}$$取最小值时,$${{x}}$$的值为()
C
A.$${{1}{9}}$$
B.$$- \frac{8} {7}$$
C.$$\begin{array} {c} {\frac{8} {7}} \\ \end{array}$$
D.$$\frac{1 9} {1 4}$$
3、['空间直角坐标系中中点坐标公式', '空间直角坐标系中两点之间的距离公式']正确率60.0%设$$A ~ ( \mathrm{\footnotesize~ ( 3, ~ 2, ~ 1 ) ~}, ~ B ~ ( \mathrm{\footnotesize~ 1, ~ 0, ~ 5 ) ~}, ~ C ~ ( \mathrm{\footnotesize~ 0, ~ 2, ~ 1 ) ~}, ~ A B$$的中点为$${{M}}$$,则$$| C M |=\langle($$)
A
A.$${{3}}$$
B.$${\sqrt {3}}$$
C.$${{2}{\sqrt {3}}}$$
D.$${{3}{\sqrt {2}}}$$
4、['空间向量运算的坐标表示', '空间直角坐标系中两点之间的距离公式', '立体几何中的动态问题']正确率40.0%如图,在正方体$$A B C D-A_{1} B_{1} C_{1} D_{1}$$中,$${{M}}$$,$${{N}}$$分别是棱$${{A}{B}}$$,$${{B}{{B}_{1}}}$$的中点,点$${{P}}$$在对角线$${{C}{{A}_{1}}}$$上运动$${{.}}$$当$${{△}{P}{M}{N}}$$的面积取得最小值时,点$${{P}}$$的位置是()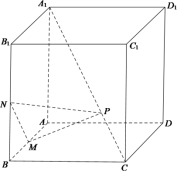
B
A.线段$${{C}{{A}_{1}}}$$的三等分点,且靠近点$${{A}_{1}}$$
B.线段$${{C}{{A}_{1}}}$$的中点
C.线段$${{C}{{A}_{1}}}$$的三等分点,且靠近点$${{C}}$$
D.线段$${{C}{{A}_{1}}}$$的四等分点,且靠近点$${{C}}$$
5、['空间直角坐标系中两点之间的距离公式']正确率60.0%在空间直角坐标系中,已知两点坐标$$A \left( 0,-4, 1 \right), \, \, \, B \left(-1,-6, 3 \right)$$,则$$| A B |=( \textsubscript{\Lambda} )$$
C
A.$${{2}}$$
B.$${\sqrt {5}}$$
C.$${{3}}$$
D.$${\sqrt {{1}{0}}}$$
6、['空间直角坐标系中两点之间的距离公式']正确率60.0%空间中两点$$A \left( 1,-1, 2 \right), \, \, \, B \left(-1, 1, 2 \sqrt{2}+2 \right)$$之间的距离是$${{(}{)}}$$
B
A.$${{3}}$$
B.$${{4}}$$
C.$${{5}}$$
D.$${{6}}$$
7、['空间直角坐标系中两点之间的距离公式']正确率80.0%在空间直角坐标系中,已知点$$A ( 2, 1, 3 ), \, \, \, B (-4, 3, 0 )$$,则$${{A}{,}{B}}$$两点间的距离是()
C
A.$${{5}}$$
B.$${{6}}$$
C.$${{7}}$$
D.$${{8}}$$
8、['空间直角坐标系中两点之间的距离公式', '立体几何中的动态问题', '用空间向量研究两条直线所成的角']正确率40.0%如图,在四面体$${{A}{B}{C}{D}}$$中,平面$${{A}{B}{C}{⊥}}$$平面$${{B}{C}{D}{,}}$$$${{△}}$$$${{B}{A}{C}}$$与$${{△}}$$$${{B}{C}{D}}$$均为等腰直角三角形,且$$\angle B A C=\angle B C D=9 0^{\circ}, \; \; B C=2,$$点$${{P}}$$在线段$${{A}{B}{(}}$$不含端点)上运动.若线段$${{C}{D}{(}}$$不含端点)上存在点$${{Q}}$$,使异面直线$${{P}{Q}}$$与$${{A}{C}}$$所成的角为$${{3}{0}^{∘}}$$,则线段$${{A}{P}}$$的长度的取值范围是()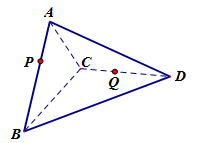
B
A.$$\left( 0, \frac{\sqrt{2}} {2} \right)$$
B.$$\left( 0, \frac{\sqrt{6}} {3} \right)$$
C.$$\left( \frac{\sqrt{2}} {2}, 2 \right)$$
D.$$\left( \frac{\sqrt{6}} {3}, 2 \right)$$
9、['空间向量运算的坐标表示', '空间直角坐标系中两点之间的距离公式']正确率60.0%$${{△}{A}{B}{C}}$$中,若$$A ~ ( \mathrm{\bf~ 2, ~ 4, ~ 3} ) ~, ~ B ~ ( \mathrm{\bf~ 4, ~ 1, ~ 9} ) ~, ~ C ~ ( \mathrm{\bf~ 1 0, ~-1, ~ 6} )$$,则该三角形的形状是()
D
A.锐角三角形
B.等边三角形
C.钝角三角形
D.等腰直角三角形
10、['空间直角坐标系中两点之间的距离公式']正确率80.0%已知空间中点$$A ( x, 1, 2 )$$和点$$B ( 2, 3, 4 ),$$且$$| A B |=2 \sqrt{3},$$则实数$${{x}}$$的值为()
A
A.$${{4}}$$或$${{0}}$$
B.$${{4}}$$
C.$${{3}}$$或$${{−}{4}}$$
D.$${{−}{3}}$$或$${{4}}$$
1.
答案:$$C$$
2.
答案:$$C$$
3.
答案:$$A$$
4.
答案:$$C$$
5.
答案:$$C$$
6.
答案:$$B$$
7.
答案:$$C$$
8.
答案:$$D$$
9.
答案:$$D$$
10.
答案:$$A$$
题目来源于各渠道收集,若侵权请联系下方邮箱.jpg)