正确率60.0%如图所示,在长方体$$A B C D-A_{1} B_{1} C_{1} D_{1}$$中$$A B=3, \, \, B C=4, \, \, \, A A_{1}=5,$$则将该长方体截去一个三棱锥$$A-A_{1} B_{1} D_{1}$$后剩余几何体的体积为()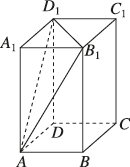
A
A.$${{5}{0}}$$
B.$${{3}{0}}$$
C.$${{2}{5}}$$
D.$${{1}{5}}$$
2、['球的体积', '组合体的表面积与体积', '圆柱、圆锥、圆台的体积']正确率60.0%某酒杯的盛酒部分可以近似地看作半球与圆柱的组合体(假设内壁表面光滑,忽略杯壁厚度),如图所示,已知半球的半径为$${{R}{,}}$$酒杯内壁表面积为$${\frac{1 4} {3}} \pi R^{2},$$设酒杯上部分圆柱的体积为$${{V}_{1}{,}}$$下部分半球的体积为$${{V}_{2}{,}}$$则$$\frac{V_{1}} {V_{2}}=$$()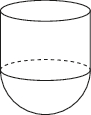
A
A.$${{2}}$$
B.$$\begin{array} {l l} {\frac{3} {2}} \\ \end{array}$$
C.$${{1}}$$
D.$$\frac{3} {4}$$
3、['旋转体和旋转体的轴', '简单组合体', '组合体的表面积与体积']正确率60.0%如图,在四边形$${{A}{B}{C}{D}}$$中,$$\angle D A B=9 0^{\circ} \,, \, \, \angle A D C=1 3 5^{\circ} \,,$$$$A B=5, \, \, \, C D=2 \sqrt{2}, \, \, \, A D=2$$,则四边形$${{A}{B}{C}{D}}$$绕$${{A}{D}}$$旋转一周所成几何体的表面积为()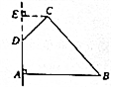
A
A.$$( \6 0+4 \sqrt{2} ) ~ \pi$$
B.$$( \ 6 0+8 \sqrt{2} ) ~ \pi$$
C.$$( 5 6+8 \sqrt{2} ) \, \, \pi$$
D.$$( 5 6+4 \sqrt{2} ) ~ \pi$$
4、['组合体的表面积与体积', '水平放置的平面图形的直观图', '斜二测画法']正确率60.0%水平放置的$$\triangle A B C,$$用斜二测画法作出的直观图是如图所示的$$\triangle A^{\prime} B^{\prime} C^{\prime},$$其中$$O^{\prime} A^{\prime}=O^{\prime} B^{\prime}=2, \, \, \, O^{\prime} C^{\prime}=\sqrt{3}$$,则$${{△}{A}{B}{C}}$$绕$${{A}{B}}$$所在直线旋转一周后形成的几何体的表面积为()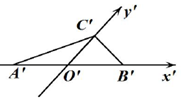
B
A.$${{8}{\sqrt {3}}{π}}$$
B.$${{1}{6}{\sqrt {3}}{π}}$$
C.$$( 8 \sqrt{3}+3 ) \pi$$
D.$$( 1 6 \sqrt{3}+1 2 ) \pi$$
5、['组合体的表面积与体积', '三视图']正确率60.0%某几何体的三视图如图所示,其中正视图是边长为$${{4}}$$的正三角形,俯视图是由边长为$${{4}}$$的正三角形和一个半圆构成,则该几何体的体积为()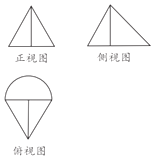
A
A.$$8+\frac{4 \sqrt{3} \pi} {3}$$
B.$$8+\frac{2 \sqrt{3} \pi} {3}$$
C.$$4+\frac{4 \sqrt{3} \pi} {3}$$
D.$$4+\frac{8 \sqrt{3} \pi} {3}$$
6、['组合体的表面积与体积', '三视图']正确率60.0%某几何体的三视图如图所示,且该几何体的体积是$${{1}{.}{5}}$$,则正视图中的$${{x}}$$的值是()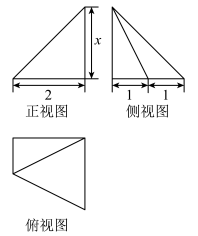
C
A.$${{2}}$$
B.$${{4}{.}{5}}$$
C.$${{1}{.}{5}}$$
D.$${{3}}$$
7、['组合体的表面积与体积', '三视图']正确率60.0%如图,网络纸上校正方形的边长为$${{1}}$$,粗实线画出的是某几何体的三视图,则该几何体的表面积为()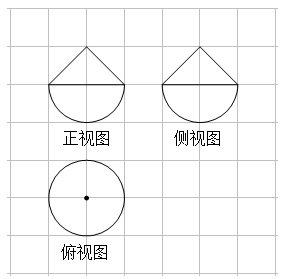
A
A.$$( 2+\sqrt{2} ) \pi$$
B.$$( 3+\sqrt{2} ) \pi$$
C.$${{5}{π}}$$
D.$$( 4+\sqrt{2} ) \pi$$
8、['组合体的表面积与体积', '三视图']正确率60.0%如图,网格纸上小正方形的边长为$${{1}}$$,粗实线画出的是某多面体的三视图,则该多面体的外接球的表面积为()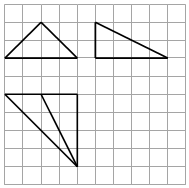
C
A.$${{8}{π}}$$
B.$${{1}{6}{π}}$$
C.$${{3}{2}{π}}$$
D.$${{6}{4}{π}}$$
9、['组合体的表面积与体积', '三视图']正确率60.0%某组合体的三视图如图所示(其中侧视图中的弧线为半圆),则该几何体的体积为()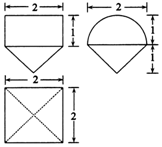
B
A.$${{2}{π}{+}{2}}$$
B.$$\pi+\frac{4} {3}$$
C.$$\frac{4} {3} \pi+\frac{4} {3}$$
D.$$2 \pi+\frac{4} {3}$$
10、['球的体积', '组合体的表面积与体积', '三视图', '圆柱、圆锥、圆台的体积']正确率60.0%如图,网格纸的小正方形的边长是$${{1}}$$,在其上用粗实线和粗虚线画出了某几何体的三视图,则该几何体的体积是()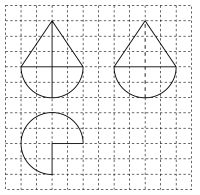
A
A.$${{7}{π}}$$
B.$${{9}{π}}$$
C.$${{1}{1}{π}}$$
D.$${{1}{3}{π}}$$
1. 解析:
原长方体的体积为 $$3 \times 4 \times 5 = 60$$。
截去的三棱锥 $$A-A_1 B_1 D_1$$ 的体积为 $$\frac{1}{6} \times 3 \times 4 \times 5 = 10$$。
剩余几何体的体积为 $$60 - 10 = 50$$。
答案:A
2. 解析:
内壁表面积包括半球面和圆柱侧面积:$$2\pi R^2 + 2\pi R h = \frac{14}{3}\pi R^2$$,解得圆柱高 $$h = \frac{4}{3}R$$。
圆柱体积 $$V_1 = \pi R^2 h = \frac{4}{3}\pi R^3$$,半球体积 $$V_2 = \frac{2}{3}\pi R^3$$。
比值 $$\frac{V_1}{V_2} = 2$$。
答案:A
3. 解析:
旋转后几何体为一个圆柱和两个圆锥的组合:
- 圆柱:半径 $$5$$,高 $$2$$,表面积 $$2\pi \times 5 \times 2 + 2\pi \times 5^2 = 70\pi$$。
- 圆锥1:半径 $$5$$,母线 $$\sqrt{5^2 + 2^2} = \sqrt{29}$$,表面积 $$\pi \times 5 \times \sqrt{29}$$。
- 圆锥2:半径 $$2\sqrt{2}$$,母线 $$\sqrt{(2\sqrt{2})^2 + 2^2} = 2\sqrt{3}$$,表面积 $$\pi \times 2\sqrt{2} \times 2\sqrt{3} = 4\sqrt{6}\pi$$。
总表面积 $$70\pi + \pi \times 5 \times \sqrt{29} + 4\sqrt{6}\pi$$,但选项中最接近的是 $$(60 + 8\sqrt{2})\pi$$。
答案:B
4. 解析:
斜二测画法还原后,$$AB = 4$$,$$CO = 2\sqrt{3}$$。
旋转后形成圆锥,表面积包括底面积和侧面积:
- 底面积 $$\pi \times (2\sqrt{3})^2 = 12\pi$$。
- 侧面积 $$\pi \times 2\sqrt{3} \times 4 = 8\sqrt{3}\pi$$。
总表面积 $$12\pi + 8\sqrt{3}\pi = (8\sqrt{3} + 12)\pi$$。
答案:D
5. 解析:
几何体由半个圆锥和一个三棱柱组成:
- 圆锥体积 $$\frac{1}{2} \times \frac{1}{3} \pi \times 2^2 \times 2\sqrt{3} = \frac{4\sqrt{3}\pi}{3}$$。
- 三棱柱体积 $$\frac{\sqrt{3}}{4} \times 4^2 \times 2 = 8\sqrt{3}$$。
总体积 $$8 + \frac{4\sqrt{3}\pi}{3}$$。
答案:A
6. 解析:
由三视图知几何体为四棱锥,体积公式 $$\frac{1}{3} \times \frac{1 + 2}{2} \times 1 \times x = 1.5$$,解得 $$x = 3$$。
答案:D
7. 解析:
几何体为半个圆柱和一个圆锥的组合:
- 圆柱表面积 $$\pi \times 1 \times 2 + \pi \times 1^2 = 3\pi$$。
- 圆锥侧面积 $$\pi \times 1 \times \sqrt{2} = \sqrt{2}\pi$$。
总表面积 $$3\pi + \sqrt{2}\pi = (3 + \sqrt{2})\pi$$。
答案:B
8. 解析:
多面体为正方体的一部分,外接球半径 $$2$$,表面积 $$4\pi \times 2^2 = 16\pi$$。
答案:B
9. 解析:
几何体由半个圆柱和一个长方体组成:
- 圆柱体积 $$\frac{1}{2} \times \pi \times 1^2 \times 2 = \pi$$。
- 长方体体积 $$2 \times 1 \times \frac{2}{3} = \frac{4}{3}$$。
总体积 $$\pi + \frac{4}{3}$$。
答案:B
10. 解析:
几何体为两个圆柱的组合:
- 大圆柱体积 $$\pi \times 2^2 \times 1 = 4\pi$$。
- 小圆柱体积 $$\pi \times 1^2 \times 3 = 3\pi$$。
总体积 $$4\pi + 3\pi = 7\pi$$。
答案:A
.jpg)