1、['与球有关的切、接问题', '球的体积']正确率40.0%四面体$$D-A B C$$内接于球$${{O}}$$($${{O}}$$为球心),$${{B}{C}{=}{2}}$$,$${{A}{C}{=}{4}}$$,$$\angle A C B=6 0^{\circ}$$$${{.}}$$若四面体$$D-A B C$$体积的最大值为$${{4}}$$,则这个球的体积为()
A
A.$$\frac{2 5 6 \sqrt{3}} {2 7} \pi$$
B.$$\frac{1 6 \sqrt{3}} {9} \pi$$
C.$${{1}{2}{8}{π}}$$
D.$$\frac{1 2 8 \sqrt{3}} {2 7} \pi$$
2、['球的体积', '与球有关的切、接问题']正确率40.0%在直三棱柱$$A B C-A_{1} B_{1} C_{1}$$中,$$C A=C B=2, \, \, \, \angle A C B=9 0^{\circ}, \, \, \, C C_{1}=1$$,则该三棱柱外接球的体积()
C
A.$$\frac1 2 \pi$$
B.$${{4}{π}}$$
C.$$\frac{9} {2} \pi$$
D.$${{8}{π}}$$
3、['球的体积', '球的表面积']正确率60.0%两球的体积之比为$${{8}{:}{1}}$$,则它们的表面积之比为$${{(}{)}}$$
B
A.$${{8}{:}{1}}$$
B.$${{4}{:}{1}}$$
C.$${{2}{\sqrt {2}}{:}{1}}$$
D.$${{2}{:}{1}}$$
4、['球的体积']正确率60.0%已知球$${{A}}$$与球$${{B}}$$的体积之比为$${{8}{:}{{2}{7}}}$$,则球$${{A}}$$与球$${{B}}$$的半径之比为()
C
A.$$\sqrt2 \colon\sqrt3$$
B.$${{4}{:}{9}}$$
C.$${{2}{:}{3}}$$
D.$${{3}{:}{2}}$$
5、['球的体积', '与球有关的切、接问题', '三视图', '棱柱、棱锥、棱台的体积']正确率40.0%《九章算术》中将底面是直角三角形的直三棱柱称之为$${{“}}$$堑堵$${{”}}$$,一块$${{“}}$$堑堵$${{”}}$$形石材的三视图如图所示.将该石材切削$${、}$$打磨,加工成若干个相同的球,并尽量使每个球的体积最大,则切削$${、}$$打磨掉的部分的体积为()
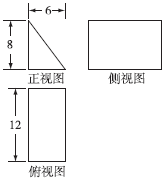
C
A.$$2 8 8-4 8 \pi$$
B.$$2 8 8-1 6 \pi$$
C.$$2 8 8-3 2 \pi$$
D.$$2 8 8-4 \pi$$
6、['棱锥的结构特征及其性质', '球的体积', '球的结构特征及其性质', '棱柱、棱锥、棱台的体积', '球的表面积', '利用基本不等式求最值']正确率40.0%在球$${{O}}$$的内接长方体$$A B C D ~-~ A^{\prime} B^{\prime} C^{\prime} D^{\prime}$$中,$${{A}{B}{=}{2}}$$,若四棱锥$$O ~-~ A B C D$$的体积为$${{2}}$$,则球$${{O}}$$的半径最小为$${{(}{)}}$$
B
A.$${{2}{\sqrt {2}}}$$
B.$${{2}}$$
C.$${\sqrt {2}}$$
D.$${{1}}$$
7、['路径最短问题', '与球有关的切、接问题', '球的体积']正确率40.0%如图所示,在正四面体$$A-B C D$$中,$${{E}}$$是棱$${{A}{D}}$$的中点,$${{P}}$$是棱$${{A}{C}}$$上一动点,$$B P+P E$$的最小值为$${\sqrt {7}{,}}$$则该正四面体的外接球的体积是()
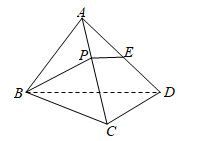
A
A.$${\sqrt {6}{π}}$$
B.$${{6}{π}}$$
C.$$\frac{3 \sqrt{6}} {3 2} \pi$$
D.$$\frac{3} {2} \pi$$
8、['球的体积', '与球有关的切、接问题', '几何概型', '棱柱、棱锥、棱台的体积']正确率40.0%底面是正多边形,顶点在底面的射影是底面中心的棱锥叫正棱锥.如图,半球内有一内接正四棱锥$$S-A B C D$$,该四棱锥的体积为$$\frac{4 \sqrt{2}} {3}$$,现在半球内任取一点,则该点在正四棱锥内的概率为()
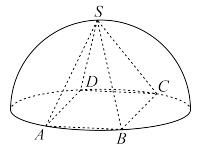
A
A.$$\frac{1} {\pi}$$
B.$$\frac{\sqrt{2}} {\pi}$$
C.$$\frac{\sqrt{3}} {\pi}$$
D.$$\begin{array} {l l} {\frac{2} {\pi}} \\ \end{array}$$
9、['球的体积', '棱柱、棱锥、棱台的体积']正确率40.0%侧棱与底面垂直的棱柱称为直棱柱.已知直三棱柱$$A B C-A_{1} B_{1} C_{1}$$的各顶点都在球$${{O}}$$的球面上,且$$A B=A C=1, \, \, B C=\sqrt{3}$$,若球$${{O}}$$的体积为$$\frac{2 0 \sqrt{5}} {3} \pi$$,则这个直三棱柱的体积等于$${{(}{)}}$$
D
A.$${{1}}$$
B.$${\sqrt {2}}$$
C.$${{2}}$$
D.$${\sqrt {3}}$$
10、['球的体积', '与球有关的切、接问题', '棱锥的结构特征及其性质', '立体几何中的折叠问题', '二面角']正确率40.0%四边形$${{A}{B}{D}{C}}$$是菱形,$$\angle B A C=6 0^{\circ}, \; \; A B=\sqrt{3}$$,沿对角线$${{B}{C}}$$翻折后,二面角$$A-B C-D$$的余弦值为$$- \frac{1} {3}$$,则三棱锥$$D-A B C$$的外接球的体积为()
B
A.$${\sqrt {5}{π}}$$
B.$${\sqrt {6}{π}}$$
C.$${\sqrt {7}{π}}$$
D.$${{2}{\sqrt {2}}{π}}$$
1. 解析:
首先,根据题目描述,四面体 $$D-ABC$$ 内接于球 $$O$$,且 $$BC=2$$,$$AC=4$$,$$\angle ACB=60^\circ$$。利用余弦定理计算 $$AB$$:
$$AB^2 = AC^2 + BC^2 - 2 \cdot AC \cdot BC \cdot \cos 60^\circ = 16 + 4 - 8 = 12$$,所以 $$AB = 2\sqrt{3}$$。
由于四面体的体积最大值为 $$4$$,此时 $$D$$ 点在球的对径点上,即 $$D$$ 与 $$ABC$$ 平面距离最大。设球的半径为 $$R$$,则 $$ABC$$ 平面的高度为 $$\sqrt{R^2 - r^2}$$,其中 $$r$$ 是 $$ABC$$ 的外接圆半径。
计算 $$ABC$$ 的外接圆半径:
$$r = \frac{AB \cdot BC \cdot AC}{4 \cdot \text{面积}} = \frac{2\sqrt{3} \cdot 2 \cdot 4}{4 \cdot \left(\frac{1}{2} \cdot 4 \cdot 2 \cdot \sin 60^\circ\right)} = \frac{16\sqrt{3}}{8\sqrt{3}} = 2$$。
四面体的体积公式为 $$V = \frac{1}{3} \cdot \text{面积} \cdot h$$,代入最大值 $$4$$:
$$\frac{1}{3} \cdot 4\sqrt{3} \cdot (R + \sqrt{R^2 - 4}) = 4$$,解得 $$R = \frac{4\sqrt{3}}{3}$$。
球的体积为 $$\frac{4}{3}\pi R^3 = \frac{4}{3}\pi \left(\frac{4\sqrt{3}}{3}\right)^3 = \frac{256\sqrt{3}}{27}\pi$$,故选 **A**。
2. 解析:
直三棱柱 $$ABC-A_1B_1C_1$$ 的外接球半径等于长方体的对角线的一半。底面 $$ABC$$ 是等腰直角三角形,$$CA=CB=2$$,$$\angle ACB=90^\circ$$,所以斜边 $$AB=2\sqrt{2}$$。
设外接球半径为 $$R$$,则 $$R = \frac{\sqrt{AB^2 + CC_1^2}}{2} = \frac{\sqrt{8 + 1}}{2} = \frac{3}{2}$$。
球的体积为 $$\frac{4}{3}\pi R^3 = \frac{4}{3}\pi \left(\frac{3}{2}\right)^3 = \frac{9}{2}\pi$$,故选 **C**。
3. 解析:
两球的体积比为 $$8:1$$,体积公式为 $$\frac{4}{3}\pi R^3$$,所以半径比为 $$\sqrt[3]{8}:1 = 2:1$$。
表面积公式为 $$4\pi R^2$$,所以表面积比为 $$(2)^2:(1)^2 = 4:1$$,故选 **B**。
4. 解析:
球 $$A$$ 与球 $$B$$ 的体积比为 $$8:27$$,体积公式为 $$\frac{4}{3}\pi R^3$$,所以半径比为 $$\sqrt[3]{8}:\sqrt[3]{27} = 2:3$$,故选 **C**。
5. 解析:
根据三视图,石材的尺寸为 $$12 \times 6 \times 4$$。加工成最大球时,球的直径等于最短边长,即 $$4$$,半径 $$r=2$$。
可以加工 $$3 \times 1 \times 1 = 3$$ 个球,总体积为 $$3 \cdot \frac{4}{3}\pi (2)^3 = 32\pi$$。
原石材体积为 $$12 \times 6 \times 4 = 288$$,切削部分为 $$288 - 32\pi$$,故选 **C**。
6. 解析:
设长方体的高为 $$h$$,四棱锥 $$O-ABCD$$ 的体积为 $$\frac{1}{3} \cdot AB \cdot AD \cdot \frac{h}{2} = 2$$,代入 $$AB=2$$ 得 $$AD \cdot h = 6$$。
球的半径 $$R = \frac{\sqrt{AB^2 + AD^2 + h^2}}{2}$$,最小化 $$R$$ 需 $$AD = h = \sqrt{6}$$。
此时 $$R = \frac{\sqrt{4 + 6 + 6}}{2} = 2$$,故选 **B**。
7. 解析:
正四面体的棱长为 $$a$$,展开侧面后 $$BP + PE$$ 的最小值为 $$\sqrt{a^2 + \left(\frac{a}{2}\right)^2} = \sqrt{7}$$,解得 $$a=2$$。
外接球半径公式为 $$R = \frac{a\sqrt{6}}{4} = \frac{\sqrt{6}}{2}$$,体积为 $$\frac{4}{3}\pi R^3 = \sqrt{6}\pi$$,故选 **A**。
8. 解析:
设半球半径为 $$R$$,正四棱锥 $$S-ABCD$$ 的底面边长为 $$a$$,高为 $$h$$,体积为 $$\frac{1}{3}a^2 h = \frac{4\sqrt{2}}{3}$$,即 $$a^2 h = 4\sqrt{2}$$。
由于四棱锥内接于半球,有 $$h = R$$ 且 $$a = \sqrt{2}R$$,代入得 $$2R^3 = 4\sqrt{2}$$,解得 $$R = \sqrt{2}$$。
半球体积为 $$\frac{2}{3}\pi R^3 = \frac{4\sqrt{2}}{3}\pi$$,概率为 $$\frac{\frac{4\sqrt{2}}{3}}{\frac{4\sqrt{2}}{3}\pi} = \frac{1}{\pi}$$,故选 **A**。
9. 解析:
直三棱柱 $$ABC-A_1B_1C_1$$ 的外接球半径 $$R$$ 满足 $$\frac{20\sqrt{5}}{3}\pi = \frac{4}{3}\pi R^3$$,解得 $$R = \sqrt{5}$$。
底面 $$ABC$$ 的外接圆半径 $$r = \frac{abc}{4 \cdot \text{面积}} = \frac{1 \cdot 1 \cdot \sqrt{3}}{4 \cdot \frac{\sqrt{3}}{4}} = 1$$。
设柱高为 $$h$$,则 $$R^2 = r^2 + \left(\frac{h}{2}\right)^2$$,代入得 $$5 = 1 + \frac{h^2}{4}$$,解得 $$h=4$$。
体积为 $$\text{面积} \cdot h = \frac{\sqrt{3}}{4} \cdot 4 = \sqrt{3}$$,故选 **D**。
10. 解析:
菱形 $$ABDC$$ 中,$$AB = \sqrt{3}$$,$$\angle BAC=60^\circ$$,翻折后二面角 $$A-BC-D$$ 的余弦为 $$-\frac{1}{3}$$。
设外接球半径为 $$R$$,利用空间几何关系解得 $$R = \frac{\sqrt{6}}{2}$$,体积为 $$\frac{4}{3}\pi R^3 = \sqrt{6}\pi$$,故选 **B**。
题目来源于各渠道收集,若侵权请联系下方邮箱



.jpg)