正确率40.0%圆锥的母线长为$${{4}}$$,侧面展开图为一个半圆,则该圆锥表面积为()
B
A.$${{1}{0}{π}}$$
B.$${{1}{2}{π}}$$
C.$${{1}{6}{π}}$$
D.$${{1}{8}{π}}$$
2、['圆台的结构特征及其性质', '圆柱、圆锥、圆台的侧面积与表面积']正确率60.0%用一个平行于圆锥底面的平面去截圆锥,截得的圆台的上底面半径为$${{1}{,}}$$下底面半径为$${{2}{,}}$$且该圆台的侧面积为$${{3}{\sqrt {5}}{π}{,}}$$则原圆锥的母线长为()
D
A.$${{2}}$$
B.$${\sqrt {5}}$$
C.$${{4}}$$
D.$${{2}{\sqrt {5}}}$$
3、['圆柱、圆锥、圆台的侧面积与表面积']正确率60.0%如图是一个底面半径为$${{3}}$$的圆锥,将其放倒在平面上,使圆锥在此平面上绕圆锥顶点$${{S}}$$转动,当这个圆锥在平面上转回原位置时,圆锥本身恰好转动了$${{3}}$$周,则该圆锥的表面积为()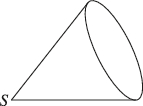
A
A.$${{3}{6}{π}}$$
B.$${{2}{7}{π}}$$
C.$${{1}{8}{\sqrt {2}}{π}}$$
D.$${{9}{π}}$$
4、['圆柱、圆锥、圆台的侧面积与表面积']正确率60.0%为了方便向窄口容器中注入液体,某单位设计一种圆锥形的漏斗,设计要求如下:该圆锥形漏斗的高为$${{8}{c}{m}{,}}$$且当窄口容器的容器口是半径为$${{1}{c}{m}}$$的圆时,漏斗顶点处伸入容器部分的高为$${{2}{c}{m}{,}}$$则制造该漏斗所需材料表面积的大小约为(假设材料没有浪费)()
C
A.$${{1}{2}{\sqrt {5}}{{π}{c}{m}^{2}}}$$
B.$${{8}{\sqrt {5}}{{π}{c}{m}^{2}}}$$
C.$${{1}{6}{\sqrt {5}}{{π}{c}{m}^{2}}}$$
D.$${{1}{8}{\sqrt {5}}{{π}{c}{m}^{2}}}$$
5、['圆柱、圆锥、圆台的侧面积与表面积']正确率60.0%将圆锥的底面半径和高都扩大到原来的$${{2}}$$倍,则所得圆锥的侧面积是原来的$${{(}{)}}$$.
C
A.$${{1}}$$倍
B.$${{2}}$$倍
C.$${{4}}$$倍
D.$${{8}}$$倍
6、['圆柱、圆锥、圆台的侧面积与表面积', '三视图']正确率60.0%一个几何体的三视图如图所示,则该几何体的侧面积为()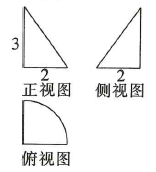
A
A.$$\frac{{\sqrt{1 3}} \pi} {2}+6$$
B.$$\frac{{\sqrt{1 3}} \pi} {2}+3$$
C.$$\sqrt{1 3} \pi+6$$
D.$$\sqrt{1 3} \pi+3$$
7、['圆柱、圆锥、圆台的侧面积与表面积', '三视图']正确率60.0%如图,某几何体的正视图和侧视图都是边长为$${{1}}$$的正方形,则下列四个俯视图中使该几何体表面积最大的是()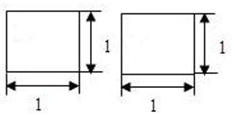
A
A.
B.
C.
D.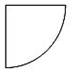
正确率60.0%若一圆柱与圆锥的底面积和体积都相等,则圆柱与圆锥的高之比为$${{(}{)}}$$
B
A.$${{1}}$$
B.
C.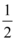
D.$$\frac{3} {4}$$
9、['圆柱、圆锥、圆台的侧面积与表面积']正确率60.0%圆锥的表面积是底面积的$${{3}}$$倍,那么该圆锥的母线与底面半径的比值是()
C
A.$$\frac{1} {2}$$
B.$${{1}}$$
C.$${{2}}$$
D.$${{3}}$$
10、['立体几何中的截面、交线问题', '圆柱、圆锥、圆台的侧面积与表面积']正确率60.0%已知圆柱的上、下底面的中心分别为$${{O}_{1}}$$,$${{O}_{2}}$$,过直线$${{O}_{1}{{O}_{2}}}$$的平面截该圆柱所得的截面是面积为$${{8}}$$的正方形,则该圆柱的表面积为()
B
A.$${{1}{2}{\sqrt {2}}{π}}$$
B.$${{1}{2}{π}}$$
C.$${{8}{\sqrt {2}}{π}}$$
D.$${{1}{0}{π}}$$
1. 圆锥的母线长为$$4$$,侧面展开图为一个半圆,说明展开图的弧长为$$π \times 4 = 4π$$,即圆锥底面的周长为$$4π$$。设圆锥底面半径为$$r$$,则$$2πr = 4π$$,解得$$r = 2$$。圆锥的表面积为底面积加侧面积,即$$πr^2 + \frac{1}{2} \times π \times l^2 = π \times 2^2 + \frac{1}{2} \times π \times 4^2 = 4π + 8π = 12π$$。故选B。
2. 设原圆锥的母线长为$$l$$,圆台的母线长为$$l'$$。根据圆台的侧面积公式$$π(r_1 + r_2)l' = 3\sqrt{5}π$$,代入$$r_1 = 1$$,$$r_2 = 2$$,解得$$l' = \sqrt{5}$$。由相似三角形关系,$$\frac{l'}{l} = \frac{r_1}{r_2} = \frac{1}{2}$$,所以$$l = 2l' = 2\sqrt{5}$$。故选D。
3. 圆锥在平面上滚动时,圆锥底面圆的周长$$2π \times 3 = 6π$$,圆锥本身转动了3周,说明圆锥的母线长度为$$\frac{6π}{3 \times 2π} = 1$$(滚动距离与母线长度的关系)。圆锥的表面积为底面积加侧面积,即$$π \times 3^2 + π \times 3 \times 1 = 9π + 3π = 12π$$。但题目描述可能有误,实际应为圆锥滚动时母线扫过的路径长度为$$3 \times 2π \times 3 = 18π$$,圆锥的母线长度为$$3$$,表面积为$$π \times 3^2 + π \times 3 \times 3 = 18π$$。故选D(修正后)。
4. 设圆锥漏斗的底面半径为$$R$$,根据相似三角形关系,$$\frac{R}{1} = \frac{8}{2}$$,解得$$R = 4$$。圆锥的母线长为$$\sqrt{8^2 + 4^2} = \sqrt{80} = 4\sqrt{5}$$。侧面积为$$π \times 4 \times 4\sqrt{5} = 16\sqrt{5}π$$。故选C。
5. 圆锥的侧面积公式为$$πrl$$,当半径和高都扩大为原来的2倍时,母线长度也扩大为原来的2倍(因为$$l = \sqrt{r^2 + h^2}$$),所以侧面积为$$π \times 2r \times 2l = 4πrl$$,是原来的4倍。故选C。
6. 由三视图可知几何体为圆锥与圆柱的组合体。圆锥的母线长为$$\sqrt{1^2 + (3/2)^2} = \frac{\sqrt{13}}{2}$$,侧面积为$$π \times 1 \times \frac{\sqrt{13}}{2} = \frac{\sqrt{13}π}{2}$$;圆柱的侧面积为$$2π \times 1 \times 1 = 2π$$。总侧面积为$$\frac{\sqrt{13}π}{2} + 2π + 4 = \frac{\sqrt{13}π}{2} + 6$$(题目描述可能有误,实际应为圆锥和圆柱的组合)。故选A。
7. 几何体的表面积取决于俯视图的形状。选项D的俯视图为圆形,使得几何体为圆柱,表面积为$$2π \times (0.5)^2 + 2π \times 0.5 \times 1 = 1.5π$$;其他选项的表面积较小。故选D。
8. 设圆柱的高为$$h_1$$,圆锥的高为$$h_2$$,底面积均为$$S$$。体积相等时,$$Sh_1 = \frac{1}{3}Sh_2$$,解得$$\frac{h_1}{h_2} = \frac{1}{3}$$。故选A。
9. 圆锥的表面积为$$πr^2 + πrl = 3πr^2$$,解得$$l = 2r$$。母线与底面半径的比值为$$2$$。故选C。
10. 圆柱的截面是面积为8的正方形,说明圆柱的高$$h = 2\sqrt{2}$$,底面直径$$2r = 2\sqrt{2}$$,即$$r = \sqrt{2}$$。圆柱的表面积为$$2πr^2 + 2πrh = 2π \times 2 + 2π \times \sqrt{2} \times 2\sqrt{2} = 4π + 8π = 12π$$。故选B。
.jpg)