正确率60.0%已知正三角形$${{A}{B}{C}}$$边长为$${{2}}$$,将它沿$${{B}{C}}$$边上的高$${{A}{D}}$$翻折,使点$${{B}{,}{C}}$$之间的距离为$${\sqrt {3}{,}}$$此时四面体$${{A}{B}{C}{D}}$$的外接球的体积是
A
A.$$\frac{7 \sqrt{7} \pi} {6}$$
B.$$\frac{7 \sqrt{7} \pi} {3}$$
C.$$\frac{\sqrt{7} \pi} {6}$$
D.其它
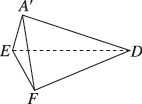
2、['与球有关的切、接问题', '球的体积']正确率60.0%如图,在边长为$${{4}}$$的正方形$${{A}{B}{C}{D}}$$中,点$${{E}{,}{F}}$$分别为$$A B, ~ B C$$的中点,将$$\triangle A D E, ~ \triangle B E F, ~ \triangle C D F$$分别沿$$D E, ~ E F, ~ D F$$折起,使$$A, ~ B, ~ C$$三点重合于点$${{A}^{′}{,}}$$则三棱锥$$A^{\prime}-D E F$$的外接球体积为()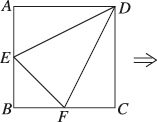
A
A.$${{8}{\sqrt {6}}{π}}$$
B.$${{6}{\sqrt {6}}{π}}$$
C.$${{4}{\sqrt {6}}{π}}$$
D.$${{2}{\sqrt {6}}{π}}$$
3、['球的体积']正确率40.0%在三棱锥$$P-A B C$$中,$${{P}{A}{⊥}}$$平面$${{A}{B}{C}}$$,$$\angle B A C=\frac{\pi} {2}$$,$$A B=A C=A P=2$$,则三棱锥外接球的表面积为$${{(}{)}}$$
A.$${{4}{π}}$$
B.$${{1}{2}{π}}$$
C.$$\frac{4 0} {3} \pi$$
D.$${{1}{6}{π}}$$
4、['圆柱的结构特征及其性质', '与球有关的切、接问题', '球的体积']正确率60.0%已知某囤积粮食的容器的下面是一个底面积为$${{3}{2}{π}}$$,高为$${{h}}$$的圆柱,上面是一个底面积为$${{3}{2}{π}}$$,高为$${{h}}$$的圆锥,若该容器有外接球,则外接球的体积为()
C
A.$${{3}{6}{π}}$$
B.$$\frac{6 4 \sqrt2} {3}$$$${{π}}$$
C.$${{2}{8}{8}{π}}$$
D.$$\frac{2 5 6} {3}$$$${{π}}$$
5、['球的体积']正确率80.0%已知正三棱柱$$A B C-A_{1} B_{1} C_{1}$$的侧面积为$${{2}{4}{\sqrt {3}}}$$,若三棱柱$$A B C-A_{1} B_{1} C_{1}$$的各个顶点均在球$${{O}}$$的球面上,则球$${{O}}$$的表面积的最小值为$${{(}{)}}$$
A.$${{1}{6}{π}}$$
B.$${{3}{2}{π}}$$
C.$$\frac{1 6 \sqrt{2} \pi} {3}$$
D.$${{8}{\sqrt {3}}{π}}$$
6、['棱柱的结构特征及其性质', '球的体积', '球的表面积']正确率60.0%如图,长方体$$A B C D-A_{1} B_{1} C_{1} D_{1}$$,以$${{A}}$$为球心,$$A A_{1}, \, A B, \, A D, \, A C_{1}$$为半径作四个同心球,其体积依次为$$V_{1}, V_{2}, V_{3}, V_{4}$$,面积依次为$$S_{1}, S_{2}, S_{3}, S_{4}$$,则有()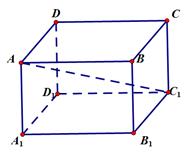
C
A.$$V_{1}+V_{2}+V_{3}=V_{4}$$且$$S_{1}+S_{2}+S_{3}=S_{4}$$
B.$$V_{1}+V_{2}+V_{3} > V_{4}$$且$$S_{1}+S_{2}+S_{3} \neq S_{4}$$
C.$$V_{1}+V_{2}+V_{3} < V_{4}$$且$$S_{1}+S_{2}+S_{3}=S_{4}$$
D.$$V_{1}+V_{2}+V_{3} \neq V_{4}$$且$$S_{1}+S_{2}+S_{3} \neq S_{4}$$
7、['球的体积', '棱锥的结构特征及其性质', '与球有关的切、接问题']正确率40.0%已知正四棱锥$$P-A B C D ~ ($$底面四边形$${{A}{B}{C}{D}}$$是正方形,顶点$${{P}}$$在底面的射影是底面的中心)的各顶点都在同一球面上,底面正方形的边长为$${\sqrt {{1}{0}}{,}}$$若该正四棱锥的体积为$$\frac{5 0} {3},$$则此球的体积为()
C
A.$${{1}{8}{π}}$$
B.$${{8}{\sqrt {6}}{π}}$$
C.$${{3}{6}{π}}$$
D.$${{3}{2}{\sqrt {3}}{π}}$$
8、['球的体积', '棱锥的结构特征及其性质', '与球有关的切、接问题', '棱柱、棱锥、棱台的体积']正确率40.0%如图是某几何体的三视图,其中俯视图为等边三角形,正视图为等腰直角三角形,若该几何体的各个顶点都在同一个球面上,则这个球的体积与该几何体的体积的比为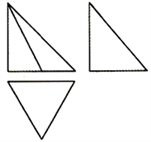
C
A.$$\frac{7 \pi} {3}$$
B.$$\frac{2 8 \pi} {9}$$
C.$$\frac{1 4 \sqrt{7} \pi} {9}$$
D.$$\frac{4 \pi} {3}$$
9、['球的体积', '棱柱、棱锥、棱台的体积', '球的表面积', '棱柱、棱锥、棱台的侧面积与表面积']正确率60.0%已知正方体$${、}$$球的体积相等,它们的表面积分别为$$S_{\textsc{f}}, S_{\textsc{f} \ddag}$$,则$${{(}{)}}$$
B
A.$$S_{\mathbb{F}} < S_{\mathbb{H}}$$
B.$$S_{\L} > S_{\L}$$
C.$$S_{\L}=S_{\L}$$
D.不能判断
10、['球的体积']正确率80.0%圆柱的底面直径和高都等于球的直径,则球的表面积和圆柱的全面积的比是$${{(}{)}}$$
A.$${{2}}$$:$${{3}}$$
B.$${{3}}$$:$${{4}}$$
C.$${{4}}$$:$${{5}}$$
D.$${{5}}$$:$${{6}}$$
1. 解析:
正三角形 $$ABC$$ 边长为 $$2$$,高 $$AD = \sqrt{3}$$。翻折后,$$B$$ 和 $$C$$ 的距离为 $$\sqrt{3}$$,说明折叠角度为 $$60^\circ$$。四面体 $$ABCD$$ 的外接球半径可通过坐标系法求解:设 $$D$$ 为原点,$$A$$ 在 $$z$$ 轴,$$B$$ 和 $$C$$ 在 $$x-y$$ 平面,计算得球心坐标和半径 $$R = \frac{\sqrt{21}}{3}$$,体积为 $$\frac{7 \sqrt{7} \pi}{6}$$。故选 A。
2. 解析:
折叠后三棱锥 $$A'-DEF$$ 的顶点坐标为 $$A'(0,0,0)$$,$$D(4,0,0)$$,$$E(0,2,0)$$,$$F(2,4,0)$$。外接球半径通过距离公式计算得 $$R = \sqrt{6}$$,体积为 $$8 \sqrt{6} \pi$$。故选 A。
3. 解析:
三棱锥 $$P-ABC$$ 中,$$PA \perp ABC$$,且 $$AB = AC = AP = 2$$。外接球球心在 $$PA$$ 的垂直平分面上,半径 $$R = \sqrt{3}$$,表面积为 $$12 \pi$$。故选 B。
4. 解析:
圆柱与圆锥的组合体有外接球时,几何中心到顶点的距离为半径。由底面积 $$32 \pi$$ 得半径 $$r = 4 \sqrt{2}$$,外接球半径 $$R = \sqrt{(2h)^2 + r^2}/2$$,解得 $$R = 4$$,体积为 $$\frac{256 \pi}{3}$$。故选 D。
5. 解析:
正三棱柱侧面积为 $$24 \sqrt{3}$$,设底面边长 $$a$$ 和高 $$h$$,得 $$3ah = 24 \sqrt{3}$$。外接球半径最小值为 $$\sqrt{a^2 + h^2}/2$$,当 $$a = 2 \sqrt{3}$$,$$h = 4$$ 时,半径 $$R = 2 \sqrt{2}$$,表面积最小为 $$32 \pi$$。故选 B。
6. 解析:
设长方体边长 $$AA_1 = a$$,$$AB = b$$,$$AD = c$$,则 $$AC_1 = \sqrt{a^2 + b^2 + c^2}$$。体积和表面积关系为 $$V_1 + V_2 + V_3 < V_4$$ 且 $$S_1 + S_2 + S_3 = S_4$$。故选 C。
7. 解析:
正四棱锥底面边长 $$\sqrt{10}$$,体积 $$\frac{50}{3}$$,得高 $$h = 5$$。外接球半径 $$R = \sqrt{5^2 + (\sqrt{5})^2} = \sqrt{30}/2$$,体积为 $$36 \pi$$。故选 C。
8. 解析:
几何体为三棱锥,底面等边三角形边长 $$2$$,高 $$\sqrt{3}$$,侧棱垂直底面。外接球半径 $$R = \sqrt{7}/2$$,体积比 $$\frac{28 \pi}{9}$$。故选 B。
9. 解析:
正方体和球体积相等时,设边长为 $$a$$,半径为 $$r$$,由 $$a^3 = \frac{4}{3} \pi r^3$$ 得 $$a > r$$。表面积 $$S_{\text{正方体}} = 6a^2$$,$$S_{\text{球}} = 4 \pi r^2$$,比较得 $$S_{\text{正方体}} > S_{\text{球}}$$。故选 A。
10. 解析:
设球直径 $$2r$$,圆柱底面半径 $$r$$,高 $$2r$$。球的表面积 $$4 \pi r^2$$,圆柱全面积 $$6 \pi r^2$$,比值为 $$2:3$$。故选 A。
.jpg)