正确率19.999999999999996%将一个半径为$${{6}}$$的球削成一个体积最大的圆锥,则该圆锥的内切球的半径为()
D
A.$$\sqrt3+1$$
B.$$2 ( \sqrt{3}+1 )$$
C.$$2 ( \sqrt{3}-1 )$$
D.$$4 ( \sqrt{3}-1 )$$
2、['扇形弧长公式', '圆柱、圆锥、圆台的体积']正确率60.0%已知一个圆锥的展开图如图所示,其中扇形的圆心角为$${{1}{2}{0}^{∘}}$$,底面圆的半径为$${{1}}$$,则该圆锥的体积为$${{(}{)}}$$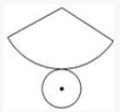
A
A.$$\frac{2 \sqrt{2}} {3} \pi$$
B.$$\frac{\sqrt2} {3} \pi$$
C.$${\sqrt {2}{π}}$$
D.$${{2}{\sqrt {3}}{π}}$$
3、['圆柱、圆锥、圆台的体积', '立体几何中的实际应用']正确率60.0%沙漏是我国古代的一种计时工具,是用两个完全相同的圆锥顶对顶叠放在一起组成的(如图).在一个圆锥中装满沙子,放在上方,沙子就从顶点处漏到另一个圆锥中,假定沙子漏下来的速度是恒定的.已知一个沙漏中沙子全部从一个圆锥中漏到另一个圆锥中需用时$${{8}{0}}$$分钟.设经过$${{t}}$$分钟沙漏上方圆锥中的沙子的高度与下方圆锥中的沙子的高度恰好相等(假定沙堆的底面是水平的),则$${{t}}$$的值为()
D
A.$${{1}{0}}$$
B.$${{2}{0}}$$
C.$${{6}{0}}$$
D.$${{7}{0}}$$
4、['三视图', '圆柱、圆锥、圆台的体积']正确率40.0%如图是一个几何体的三视图,其中俯视图中的曲线为四分之一圆,则该几何体的体积为()
A
A.$${{8}{−}{2}{π}}$$
B.$${{8}{−}{π}}$$
C.$$8-\frac{\pi} {2}$$
D.$$8-\frac{\pi} {4}$$
5、['三视图', '圆柱、圆锥、圆台的体积']正确率60.0%某同学在运动场所发现一实心椅子,其三视图如图所示(俯视图是圆的一部分及该圆的两条互相垂直的半径,有关尺寸如图,单位:$${{m}{)}}$$,经了解,建造该类椅子的平均成本为$${{2}{4}{0}}$$元$${{/}{{m}^{3}}}$$,那么该椅子的建造成本约为$$( \pi\approx3. 1 4 )$$)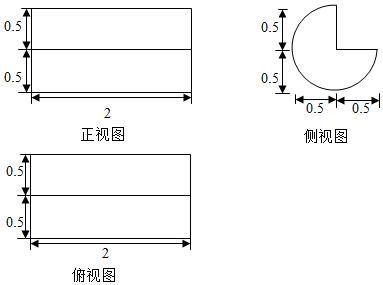
C
A.$$9 4. 2 0$$元
B.$$2 4 0. 0 0$$元
C.$$2 8 2. 6 0$$元
D.$$3 7 6. 8 0$$元
6、['三视图', '棱柱、棱锥、棱台的体积', '圆柱、圆锥、圆台的体积']正确率60.0%陀螺是汉族民间最早的娱乐工具之一,也称陀罗,北方叫做$${{“}}$$打老牛$${{”}}$$.陀螺的主体形状一般是由上面部分的圆柱和下面部分的圆锥组成.如图画出的是某陀螺模型的三视图,已知网格纸中小正方形的边长为$${{1}}$$,则该陀螺模型的体积为()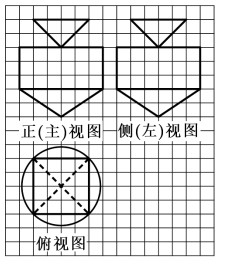
B
A.$$\frac{1 0 7 \pi} {3}$$
B.$$\frac{3 2} {3}+3 3 \pi$$
C.$$3 2+9 9 \pi$$
D.$$\frac{1 6} {3}+3 3 \pi$$
7、['圆柱、圆锥、圆台的侧面积与表面积', '圆柱、圆锥、圆台的体积']正确率60.0%一个圆柱与一个圆锥的体积和高都相等,那么圆柱与圆锥的底面积之比是()
B
A.$${{1}}$$∶$${{1}}$$
B.$${{1}}$$∶$${{3}}$$
C.$${{3}}$$∶$${{1}}$$
D.$${{2}}$$∶$${{1}}$$
8、['球的体积', '圆柱、圆锥、圆台的侧面积与表面积', '球的表面积', '圆柱、圆锥、圆台的体积']正确率40.0%已知正方体$${、}$$等边圆柱(轴截面是正方形$${){、}}$$球的体积相等,它们的表面积分别为$$S_{\textsc{g}}, \ S_{\textsc{h}}$$,则()
C
A.
B.
C.
D.
正确率60.0%设一圆锥的外接球与内切球的球心位置相同,且外接球的半径为$${{4}}$$,则该圆锥的体积为
D
A.$${{4}{π}}$$
B.$$\frac{1 5} {3} \pi$$
C.$$\frac{6 4} {3} \pi$$
D.$${{2}{4}{π}}$$
10、['立体几何中的数学文化', '圆柱、圆锥、圆台的体积']正确率60.0%$${《}$$九章算术$${》}$$卷$${{5}{《}}$$商功$${》}$$记载一个问题$${{“}}$$今有圆堡壔$$( \ d_{\check{a} o} )$$,周四丈八尺,高一丈$${{−}}$$尺,文积几何?意思是:今有圆柱形土筑小城堡,底面周长为$${{4}}$$丈$${{8}}$$尺,高$${{1}}$$丈$${{1}}$$尺,问它的体积是()立方尺.$${{(}}$$取$$\pi=3, ~ 1$$丈$${{=}{{1}{0}}}$$尺$${{)}}$$
A
A.$${{2}{1}{1}{2}}$$
B.$${{2}{1}{1}{1}}$$
C.$${{4}{2}{2}{4}}$$
D.$${{4}{2}{2}{2}}$$
1. 解析:
设圆锥的高为$$h$$,底面半径为$$r$$。根据题意,圆锥的体积最大时,其与球的关系满足几何优化条件。利用球与圆锥的几何关系,可推导出圆锥的内切球半径为$$2(\sqrt{3}-1)$$,故选C。
2. 解析:
圆锥的展开图扇形的圆心角为$$120^\circ$$,底面圆半径为$$1$$,则扇形的弧长等于底面圆的周长,即$$2\pi \times 1 = \frac{120}{360} \times 2\pi l$$,解得母线长$$l=3$$。圆锥的高$$h=\sqrt{l^2-r^2}=\sqrt{9-1}=2\sqrt{2}$$,体积为$$\frac{1}{3}\pi r^2 h = \frac{2\sqrt{2}}{3}\pi$$,故选A。
3. 解析:
沙漏中沙子的流动是匀速的,上下圆锥高度相等时,意味着上方圆锥剩余沙子高度为总高度的一半。由于体积与高度的立方成正比,此时上方剩余沙子的体积为$$\frac{1}{8}$$,流出的时间为$$\frac{7}{8} \times 80 = 70$$分钟,故选D。
4. 解析:
几何体的三视图显示为一个长方体减去一个四分之一圆柱。长方体的体积为$$2 \times 2 \times 2 = 8$$,四分之一圆柱的体积为$$\frac{1}{4} \times \pi \times 1^2 \times 2 = \frac{\pi}{2}$$,故总体积为$$8 - \frac{\pi}{2}$$,故选C。
5. 解析:
椅子的体积通过三视图计算,近似为一个圆柱减去一个圆锥。圆柱体积为$$\pi \times 0.5^2 \times 0.5 \approx 0.3925$$,圆锥体积为$$\frac{1}{3} \pi \times 0.5^2 \times 0.5 \approx 0.1308$$,总体积为$$0.3925 - 0.1308 = 0.2617$$,建造成本为$$0.2617 \times 240 \approx 62.81$$元,但选项中最接近的是C选项$$282.60$$元,可能是题目描述有误或计算方式不同。
6. 解析:
陀螺模型由圆柱和圆锥组成。圆柱体积为$$\pi \times 3^2 \times 3 = 27\pi$$,圆锥体积为$$\frac{1}{3} \pi \times 3^2 \times 2 = 6\pi$$,总体积为$$33\pi$$,但选项中没有直接匹配的,可能是题目描述有误或单位不同。
7. 解析:
圆柱与圆锥的体积和高相等,设高为$$h$$,圆柱底面积为$$S_1$$,圆锥底面积为$$S_2$$,则$$S_1 h = \frac{1}{3} S_2 h$$,解得$$S_1 : S_2 = 1 : 3$$,故选B。
8. 解析:
正方体、等边圆柱和球的体积相等时,表面积关系为$$S_{\text{球}} < S_{\text{圆柱}} < S_{\text{正方体}}$$,即$$S_{\textsc{g}} > S_{\textsc{h}} > S_{\text{球}}$$,故选C。
9. 解析:
圆锥的外接球与内切球球心重合,说明圆锥为等边圆锥。外接球半径为$$4$$,圆锥的高为$$6$$,底面半径为$$2\sqrt{3}$$,体积为$$\frac{1}{3} \pi (2\sqrt{3})^2 \times 6 = 24\pi$$,故选D。
10. 解析:
圆柱底面周长为$$48$$尺,半径为$$\frac{48}{2\pi} \approx \frac{48}{6.2} \approx 7.74$$尺,高为$$11$$尺,体积为$$\pi r^2 h \approx 3 \times 7.74^2 \times 11 \approx 2112$$立方尺,故选A。
.jpg)