.jpg)
正确率60.0%已知某圆台的高为$${{2}{\sqrt {2}}{，}}$$上底面半径为$${{1}{，}}$$下底面半径为$${{2}{，}}$$则其侧面展开图的面积为（）
A
A.$${{9}{π}}$$
B.$${{6}{\sqrt {2}}{π}}$$
C.$${{9}{\sqrt {2}}{π}}$$
D.$${{8}{π}}$$
2、['点到平面的距离'， '圆柱、圆锥、圆台的侧面积与表面积']正确率40.0%已知等边三角形$${{S}{A}{B}}$$为圆锥的轴截面$${，{A}{B}}$$为圆锥的底面直径$${，{O}{，}{C}}$$分别是$$A B， \ S B$$的中点，过$${{O}{C}}$$且与平面$${{S}{A}{B}}$$垂直的平面记为$${{α}{，}}$$若点$${{S}}$$到平面$${{α}}$$的距离为$${\sqrt {6}{，}}$$则该圆锥的侧面积为（）
B
A.$${{8}{π}}$$
B.$${{1}{6}{π}}$$
C.$${{2}{4}{π}}$$
D.$${{3}{2}{π}}$$
3、['圆锥的结构特征及其性质'， '圆柱、圆锥、圆台的侧面积与表面积']正确率60.0%圆锥的表面积是底面积的$${{4}}$$倍，那么该圆锥的侧面展开图的圆心角为（）
A
A.$${{1}{2}{0}^{∘}}$$
B.$${{1}{3}{5}^{∘}}$$
C.$${{1}{5}{0}^{∘}}$$
D.$${{1}{8}{0}^{∘}}$$
4、['圆锥的结构特征及其性质'， '圆柱、圆锥、圆台的侧面积与表面积'， '圆柱、圆锥、圆台的体积']正确率60.0%甲，乙两个圆锥的母线长相等，侧面展开图的圆心角之和为$${{2}{π}}$$，侧面积分别为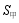
和$$S_{\mathrm{z}}$$，体积分别为
和$$V_{\mathrm{Z}}$$，若$$\frac{S_{\natural}} {S_{\natural}}=2$$，则$$\frac{V_{\mp}} {V_{\mathrm{z}}}=$$（）
C
A.$${\sqrt {5}}$$
B.$${{2}{\sqrt {2}}}$$
C.$${\sqrt {{1}{0}}}$$
D.$$\frac{5 \sqrt{1 0}} {4}$$
5、['圆柱、圆锥、圆台的侧面积与表面积'， '三视图']正确率60.0%一个机器零件的三视图如图所示，其中侧视图是一个半圆与边长为$${{a}}$$的正方形，俯视图是一个半圆内切于边长为$${{a}}$$的正方形．若该机器零件的表面积为$$9 6+4 \pi$$，则$${{a}}$$的值为（）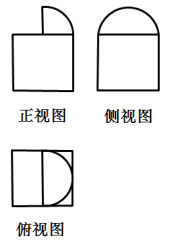
A
A.$${{4}}$$
B.$${{2}}$$
C.$${{8}}$$
D.$${{6}}$$
6、['圆柱、圆锥、圆台的侧面积与表面积'， '圆柱、圆锥、圆台的体积']正确率60.0%将一个体积为$${{3}{6}{π}}$$的金属球切割加工成一个底面积为$${{8}{π}}$$的圆柱，则当圆柱的体积最大时，其侧面积为（）
A
A.$${{8}{\sqrt {2}}{π}}$$
B.$${{8}{\sqrt {3}}{π}}$$
C.$${{6}{\sqrt {2}}{π}}$$
D.$${{9}{\sqrt {3}}{π}}$$
7、['与球有关的切、接问题'， '圆柱、圆锥、圆台的侧面积与表面积']正确率60.0%球的半径为$${{2}}$$，它的内接圆柱的底面半径为$${{1}}$$，则圆柱的侧面积为$${{(}{)}}$$
B
A.$${{2}{\sqrt {3}}{π}}$$
B.$${{4}{\sqrt {3}}{π}}$$
C.$${{1}{2}{π}}$$
D.$${{2}{4}{π}}$$
8、['圆锥的结构特征及其性质'， '圆柱、圆锥、圆台的侧面积与表面积']正确率60.0% 若一个圆锥的轴截面是面积为 $${{2}}$$ 的等腰直角三角形，则该圆锥的侧面积为 $${{(}{)}}$$
B
A.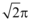
B.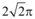
C.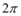
D.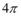
正确率60.0%已知圆锥的顶点为$${{S}}$$，底面圆周上的两点$${{A}{、}{B}}$$满足$${{Δ}{S}{A}{B}}$$为等边三角形，且面积为$${{4}{\sqrt {3}}}$$，又知$${{S}{A}}$$与圆锥底面所成的角为$${{4}{5}^{∘}}$$，则圆锥的表面积为（）
C
A.$${{8}{\sqrt {2}}{π}}$$
B.$$4 ( \sqrt{2}+2 ) \pi$$
C.$$8 ( \sqrt{2}+1 ) \pi$$
D.$$8 ( \sqrt{2}+2 ) \pi$$
10、['与球有关的切、接问题'， '圆柱、圆锥、圆台的侧面积与表面积'， '三视图']正确率60.0%已知一个几何体的主视图及左视图均是边长为$${{2}}$$的正三角形，俯视图是直径为$${{2}}$$的圆，则此几何体的外接球的表面积为（）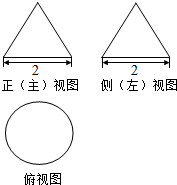
C
A.$$\frac{4} {3} \pi$$
B.$$\frac{8} {3} \pi$$
C.$$\frac{1 6} {3} \pi$$
D.$$\frac{3 2} {3} \pi$$
1. 圆台的侧面展开图是一个扇环，其面积公式为 $$π(R + r)l$$，其中 $$R$$ 和 $$r$$ 分别为下底和上底半径，$$l$$ 为母线长。首先计算母线长：
2. 设圆锥底面半径为 $$r$$，母线长为 $$l$$。由于轴截面为等边三角形，$$l = 2r$$。建立坐标系，计算平面 $$α$$ 的方程，利用点到平面距离公式解得 $$r = 2$$，进而圆锥侧面积为 $$πrl = 8π$$，答案为 A。
3. 圆锥表面积是底面积的 4 倍，即 $$πr^2 + πrl = 4πr^2$$，解得 $$l = 3r$$。展开图圆心角为 $$\frac{r}{l} \times 360^\circ = 120^\circ$$，答案为 A。
4. 设母线长为 $$l$$，甲、乙圆锥的展开图圆心角分别为 $$θ_1$$ 和 $$θ_2$$，由题意 $$θ_1 + θ_2 = 2π$$。侧面积比为 2，解得 $$θ_1 = \frac{4π}{3}$$，$$θ_2 = \frac{2π}{3}$$。进一步求得体积比为 $$\sqrt{10}$$，答案为 C。
5. 表面积为 $$2a^2 + 2π\left(\frac{a}{2}\right)^2 + πa^2 = 96 + 4π$$，解得 $$a = 4$$，答案为 A。
6. 球半径为 $$R = 3$$。设圆柱高为 $$h$$，由几何关系得 $$h = 2\sqrt{9 - r^2}$$。体积最大时 $$r = 2$$，侧面积为 $$8\sqrt{2}π$$，答案为 A。
7. 圆柱的高 $$h = 2\sqrt{4 - 1} = 2\sqrt{3}$$，侧面积为 $$2π \times 1 \times 2\sqrt{3} = 4\sqrt{3}π$$，答案为 B。
8. 轴截面为等腰直角三角形，面积为 2，解得半径 $$r = \sqrt{2}$$，母线 $$l = 2$$，侧面积为 $$2\sqrt{2}π$$，答案为 B。
9. 由等边三角形面积得边长 $$SA = 4$$。因 $$SA$$ 与底面成 45°，圆锥高 $$h = 2\sqrt{2}$$，半径 $$r = 2\sqrt{2}$$。表面积为 $$8(1 + \sqrt{2})π$$，答案为 C。
10. 几何体为圆锥，底面半径 1，高 $$\sqrt{3}$$。外接球半径 $$R = \frac{2}{\sqrt{3}}$$，表面积 $$\frac{16}{3}π$$，答案为 C。
题目来源于各渠道收集，若侵权请联系下方邮箱