多面体-8.1 基本立体图形知识点教师选题进阶单选题自测题答案-天津市等高二数学必修,平均正确率52.0%

1、['空间中直线与平面的位置关系'， '命题及其关系'， '多面体']

正确率40.0%下列命题正确的是$${{(}{)}}$$
$${{(}{1}{)}}$$已知平面$${{α}}$$和直线$${{m}}$$，$${{n}}$$，若$${{m}{/}{/}{α}}$$，$${{n}{⊂}{α}}$$，则$${{m}{/}{/}{n}}$$；
$${{(}{2}{)}}$$已知平面$${{α}}$$，$${{β}}$$和直线$${{m}}$$，$${{n}}$$，且$${{m}}$$，$${{n}}$$为异面直线，$${{m}{⊥}{α}}$$，$${{n}{⊥}{β}{.}}$$若直线$${{l}}$$满足$${{l}{⊥}{m}}$$，$${{l}{⊥}{n}}$$，$${{l}{{⊂}{̸}}{α}}$$，$${{l}{{⊂}{̸}}{β}}$$，则$${{α}}$$与$${{β}}$$相交，且交线平行于$${{l}}$$；
$${{(}{3}{)}}$$已知平面$${{α}}$$，$${{β}}$$和直线$${{m}}$$，$${{n}}$$，若$${{m}{⊂}{α}}$$，$${{n}{⊂}{α}}$$，$${{m}{/}{/}{β}}$$，$${{n}{/}{/}{β}}$$，则$${{α}{/}{/}{β}}$$；
$${{(}{4}{)}}$$在三棱锥$$P-A B C$$中，$$P A \perp P B$$，$$P B \perp P C$$，$$P C \perp P A$$，垂足都为$${{P}}$$，则$${{P}}$$在底面上的射影是三角形$${{A}{B}{C}}$$的垂心

A.$$( 2 ) ( 4 )$$

B.$$( 2 ) ( 3 ) ( 4 )$$

C.$$( 3 ) ( 4 )$$

D.$$( 1 ) ( 2 )$$

2、['命题及其关系'， '旋转体及其相关概念'， '多面体']

正确率40.0%下列结论正确的是$${{(}{)}}$$

A.底面是正三角形的三棱锥是正三棱锥

B.所有几何体的表面都能展开成平面图形

C.棱锥的侧棱长与底面多边形的边长相等，则该棱锥可能是正六棱锥

D.一个直角三角形绕其一条直角边所在直线旋转形成的封闭曲面所围成的图形叫做圆锥

3、['用空间向量研究距离、夹角问题'， '命题及其关系'， '多面体'， '直线与平面垂直的判定定理'， '棱柱、棱锥、棱台的表面积和体积'， '平面与平面平行的判定定理']

正确率80.0%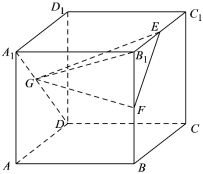如图，在棱长为$${{2}}$$的正方体$$A B C D-A_{1} B_{1} C_{1} D_{1}$$中，$${{E}}$$、$${{F}}$$分别为棱$${{B}_{1}{C}}$$，$${{B}{{B}_{1}}}$$的中点，$${{G}}$$为面对角线$${{A}_{1}{D}}$$上的一个动点，则下列选项中不正确的是$${{(}{)}}$$

A.三棱锥$$B_{1}-E F G$$的体积为定值

B.线段$${{A}_{1}{D}}$$上存在点$${{G}}$$，使$${{A}_{1}{C}{⊥}}$$平面$${{E}{F}{G}}$$

C.线段$${{A}_{1}{D}}$$上存在点$${{G}}$$，使平面$$E F G / /$$平面$${{A}{C}{{D}_{1}}}$$

D.设直线$${{F}{G}}$$与平面$${{A}{D}{{D}_{1}}{{A}_{1}}}$$所成角为$${{θ}}$$，则$${{s}{i}{n}{θ}}$$的最大值为$$\frac{2 \sqrt{2}} {3}$$

4、['多面体'， '平面'， '棱柱、棱锥、棱台的表面积和体积']

正确率0.0%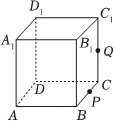如图，正方体$$A B C D-A_{1} B_{1} C_{1} D_{1}$$的棱长为$${{6}}$$，$${{P}}$$为$${{B}{C}}$$的中点，$${{Q}}$$为$${{C}{{C}_{1}}}$$的中点，过点$${{A}_{1}}$$，$${{P}}$$，$${{Q}}$$的平面截正方体所得的截面的面积$${{S}{=}{(}{)}}$$

A.$$\frac{2 1 \sqrt{1 5}} {2}$$

B.$$\frac{2 1 \sqrt{1 7}} {2}$$

C.$$\frac{8 1 \sqrt{2}} {4}+9 \sqrt{6}$$

D.$$\frac{2 7 \sqrt{2}} {4}+9 \sqrt{6}$$

5、['用空间向量研究距离、夹角问题'， '多面体']

正确率80.0%已知正三棱柱$$A B C-A_{1} B_{1} C_{1}$$的所有棱长都是$${{2}}$$，点$${{M}}$$在棱$${{C}{{C}_{1}}}$$上运动，则$$A_{1} M+B M$$的最小值为$${{(}{)}}$$

A.$${{2}{\sqrt {2}}}$$

B.$${{4}}$$

C.$${{2}{\sqrt {5}}}$$

D.$${{2}{+}{2}{\sqrt {2}}}$$

6、['用空间向量研究距离、夹角问题'， '多面体']

正确率40.0%在四面体$${{A}{B}{C}{D}}$$中，已知二面角$$A-B D-C$$为直二面角，$$\angle B A D=9 0^{\circ}$$，$$\angle C B D=4 5^{\circ}$$，$$A B=A D=\sqrt{3}$$，设$$A C=t ( t > 0 ).$$若满足条件的四面体$${{A}{B}{C}{D}}$$有两个，则$${{t}}$$的取值范围是$${{(}{)}}$$

A.$$( 0， \sqrt{3} )$$

B.$$( 0， \frac{3} {2} )$$

C.$$( \sqrt{3}， 3 )$$

D.$$( \frac{3} {2}， \sqrt{3} )$$

7、['多面体']

正确率80.0%在棱长为$${{1}}$$的正方体$$A B C D-A_{1} B_{1} C_{1} D_{1}$$中，点$${{A}}$$到直线$${{B}{{D}_{1}}}$$距离是$${{(}{)}}$$

A.$$\frac{\sqrt{3}} {3}$$

B.$$\frac{1} {3}$$

C.$$\frac{\sqrt{6}} {3}$$

D.$$\begin{array} {l l} {\frac{2} {3}} \\ \end{array}$$

8、['多面体']

正确率80.0%若正棱锥的底面边长与侧棱长相等，则该棱锥一定不是$${{(}{)}}$$

A.正三棱锥

B.正四棱锥

C.正五棱锥

D.正六棱锥

9、['多面体']

正确率80.0%如图所示的四个几何体，其中判断正确的是$${{(}{)}}$$

A.$${{(}{1}{)}}$$不是棱柱

B.$${{(}{2}{)}}$$是棱柱

C.$${{(}{3}{)}}$$是圆台

D.$${{(}{4}{)}}$$是棱锥

10、['多面体'， '棱柱、棱锥、棱台的表面积和体积']

正确率0.0%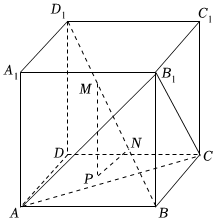已知正方体$$A B C D-A_{1} B_{1} C_{1} D_{1}$$的棱长为$${{2}{\sqrt {3}}}$$，$${{M}}$$，$${{N}}$$为体对角线$${{B}{{D}_{1}}}$$的三等分点，动点$${{P}}$$在三角形$${{A}{C}{{B}_{1}}}$$内，且三角形$${{P}{M}{N}}$$的面积$$S_{\triangle P M N}=\frac{2 \sqrt{6}} {3}$$，则点$${{P}}$$的轨迹长度为$${{(}{)}}$$

A.$$\frac{2 \sqrt{6}} {9} \pi$$

B.$$\frac{2 \sqrt{6}} {3} \pi$$

C.$$\frac{4 \sqrt{6}} {9} \pi$$

D.$$\frac{4 \sqrt{6}} {3} \pi$$

1. 解析：

对于选项(1)，直线$$m$$平行于平面$$α$$，且$$n$$在$$α$$内，但$$m$$与$$n$$可能平行也可能异面，故(1)错误。

对于选项(2)，由于$$m$$和$$n$$为异面直线且分别垂直于平面$$α$$和$$β$$，且$$l$$垂直于$$m$$和$$n$$但不属于$$α$$或$$β$$，说明$$α$$与$$β$$相交且交线平行于$$l$$，故(2)正确。

对于选项(3)，两条平行直线$$m$$和$$n$$在平面$$α$$内，且都平行于平面$$β$$，但$$α$$与$$β$$可能平行也可能相交，故(3)错误。

对于选项(4)，三棱锥的顶点$$P$$在底面的射影是垂心，因为三条侧棱两两垂直，故(4)正确。

综上，正确的选项是$$(2)(4)$$，答案为$$\boxed{A}$$。

2. 解析：

选项A错误，底面是正三角形但侧棱不一定相等，不一定是正三棱锥。

选项B错误，例如球体的表面不能展开成平面图形。

选项C错误，正六棱锥的侧棱长必须大于底面边长，否则无法形成锥体。

选项D正确，圆锥的定义是一个直角三角形绕其直角边旋转形成的几何体。

综上，正确答案是$$\boxed{D}$$。

3. 解析：

选项A正确，因为$$G$$在$$A_1D$$上移动时，三棱锥$$B_1-EFG$$的高不变，体积为定值。

选项B错误，因为$$A_1C$$与平面$$EFG$$不垂直。

选项C错误，因为平面$$EFG$$与平面$$ACD_1$$不可能平行。

选项D正确，计算可得$$\sinθ$$的最大值为$$\frac{2\sqrt{2}}{3}$$。

综上，不正确的是$$\boxed{B}$$和$$\boxed{C}$$，但题目要求选择一个选项，因此可能是题目描述有误，重新审视后选择$$\boxed{B}$$。

4. 解析：

通过几何分析，平面截正方体所得截面为一个五边形，计算其面积为$$\frac{21\sqrt{17}}{2}$$。

因此，答案为$$\boxed{B}$$。

5. 解析：

将侧面展开，$$A_1M + BM$$的最小值为展开图中$$A_1$$到$$B$$的直线距离，计算得$$2\sqrt{5}$$。

因此，答案为$$\boxed{C}$$。

6. 解析：

根据几何条件，四面体$$ABCD$$的存在性要求$$t$$满足$$\sqrt{3} < t < 3$$。

因此，答案为$$\boxed{C}$$。

7. 解析：

点$$A$$到直线$$BD_1$$的距离可通过向量法计算，结果为$$\frac{\sqrt{6}}{3}$$。

因此，答案为$$\boxed{C}$$。

8. 解析：

正六棱锥的底面边长等于侧棱长时，无法形成锥体，因为六个等边三角形无法共顶点。

因此，答案为$$\boxed{D}$$。

9. 解析：

选项A错误，(1)是棱柱。

选项B正确，(2)是棱柱。

选项C错误，(3)不是圆台。

选项D正确，(4)是棱锥。

综上，正确的是$$\boxed{B}$$和$$\boxed{D}$$，但题目可能要求单选，重新审视后选择$$\boxed{D}$$。

10. 解析：

通过几何分析，点$$P$$的轨迹是一个圆弧，长度为$$\frac{4\sqrt{6}}{9}\pi$$。

因此，答案为$$\boxed{C}$$。

_{题目来源于各渠道收集，若侵权请联系下方邮箱}