正确率40.0%下列命题中错误的是()
B
A.圆柱的轴截面是过母线的截面中面积最大的一个
B.圆锥的轴截面是所有过顶点的截面中面积最大的一个
C.圆台的所有平行于底面的截面都是圆
D.圆锥所有的轴截面是全等的等腰三角形
2、['旋转体和旋转体的轴', '组合体的表面积与体积', '圆柱、圆锥、圆台的侧面积与表面积', '圆柱、圆锥、圆台的体积']正确率60.0%已知直角三角形$${{A}{B}{C}}$$,其三边分为$$a, \; b, \; c, \; \; ( a > b > c )$$。分别以三角形的$${{a}}$$边,$${{b}}$$边,$${{c}}$$边所在直线为轴,其余各边旋转一周形成的曲面围成三个几何体,其表面积和体积分别为$$S_{1}, ~ S_{2}, ~ S_{3}$$和$$V_{1} \,, \, \, V_{2} \,, \, \, V_{3}$$.则它们的关系为 ()
B
A.$$S_{1} > S_{2} > S_{3}, \, \, \, V_{1} > V_{2} > V_{3}$$
B.$$S_{1} < S_{2} < S_{3}, \, \, \, V_{1} < V_{2} < V_{3}$$
C.$$S_{1} > S_{2} > S_{3}, \, \, \, V_{1}=V_{2}=V_{3}$$
D.$$S_{1} < S_{2} < S_{3}, \, \, \, V_{1}=V_{2}=V_{3}$$
3、['旋转体和旋转体的轴', '球的体积', '祖暅原理及其应用']正确率40.0%$${《}$$九章算术$${》}$$中记载了我国古代数学家祖暅在计算球的体积中使用的一个原理:$${{“}}$$幂势既同,则积不异$${{”}}$$,此即祖暅原理,其含义为:两个同高的几何体,如在等高处的截面的面积恒相等,则它们的体积相等.如图,设满足不等式组$$\left\{\begin{matrix} {x^{2}-4 y \geqslant} \\ {| x | \leqslant4} \\ {y \geq0} \\ \end{matrix} \right.$$的点$$( \ x, \ y )$$组成的图形(图$${({1}{)}}$$中的阴影部分)绕$${{y}}$$轴旋转$${{1}{8}{0}^{∘}}$$,所得几何体的体积为$${{V}_{1}}$$;满足不等式组$$\left\{\begin{array} {l l} {x^{2}+y^{2} \leqslant1 6} \\ {x^{2}+( y-2 )^{2} \geqslant4 \;.} \\ {y \geqslant0} \\ \end{array} \right.$$的点$$( \ x, \ y )$$组成的图形(图$${({2}{)}}$$中的阴影部分)绕$${{y}}$$轴旋转$${{1}{8}{0}^{∘}}$$,所得几何体的体积为$${{V}_{2}}$$.利用祖暅原理,可得$${{V}_{1}{=}{(}}$$)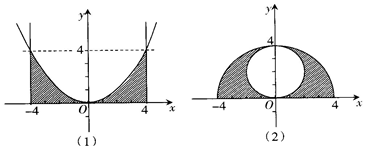
C
A.$$\frac{3 2} {3} \pi$$
B.$$\frac{6 4} {3} \pi$$
C.$${{3}{2}{π}}$$
D.$${{6}{4}{π}}$$
4、['旋转体和旋转体的轴']正确率80.0%图可由哪个平面图形旋转得到()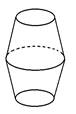
C
A.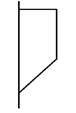
B.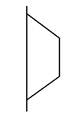
C.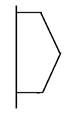
D.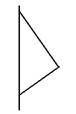
正确率60.0%已知矩形$$A B C D, \, \, \, A B=6, \, \, \, B C=8$$,沿矩形的对角线$${{A}{C}}$$将平面$${{A}{C}{D}}$$折起,若$$A, ~ B, ~ C, ~ D$$四点都在同一球面上,则该球面的面积为()
C
A.$${{3}{6}{π}}$$
B.$${{6}{4}{π}}$$
C.$${{1}{0}{0}{π}}$$
D.$${{2}{0}{0}{π}}$$
6、['旋转体和旋转体的轴', '圆锥的结构特征及其性质']正确率60.0%将锐角三角形绕其一边旋转一周所形成的空间几何体是()
D
A.一个圆柱
B.一个圆锥
C.一个圆台
D.两个圆锥的组合体
7、['旋转体和旋转体的轴', '棱台的结构特征及其性质', '棱锥的结构特征及其性质', '圆锥的结构特征及其性质', '球的结构特征及其性质']正确率40.0%下列命题中,正确的个数是$${{(}{)}}$$
$${①}$$棱台上$${、}$$下底面是相似多边形,并且互相平行;
$${②}$$若正棱锥的底面边长与侧棱长相等,则该棱锥可以是六棱锥;
$${③}$$直角三角形绕一边所在直线旋转得到的旋转体是圆锥;
$${④}$$球是空间中到一定点的距离等于定长的点的集合。
A
A.$${{1}}$$个
B.$${{2}}$$个
C.$${{3}}$$个
D.$${{4}}$$个
8、['旋转体和旋转体的轴', '圆柱、圆锥、圆台的侧面积与表面积']正确率60.0%已知$${{△}{A}{B}{C}}$$中,$$A B=4, \, \, B C=3, \, \, \, A C=5$$,现以$${{A}{B}}$$为轴旋转一周,则所得几何体的侧面积为()
C
A.$${{9}{π}}$$
B.$${{1}{2}{π}}$$
C.$${{1}{5}{π}}$$
D.$${{2}{4}{π}}$$
9、['旋转体和旋转体的轴', '*复数乘法几何意义初探']正确率60.0%在复平面内,复数$$- \frac1 2+\frac{\sqrt3} 2 i$$对应的点为$${{Z}}$$,将点$${{Z}}$$绕原点逆时针旋转$${{9}{0}^{∘}}$$后得到点$${{Z}^{′}}$$,则$${{Z}^{′}}$$对应的复数是
C
A.$$- \frac1 2+\frac{\sqrt3} 2 i$$
B.$$\frac1 2-\frac{\sqrt3} 2 i$$
C.$$- \frac{\sqrt{3}} {2}+\frac{1} {2} i$$
D.$$\frac{\sqrt{3}} {2}-\frac{1} {2} i$$
10、['圆柱的结构特征及其性质', '旋转体和旋转体的轴', '球的结构特征及其性质', '圆柱、圆锥、圆台的侧面积与表面积', '球的表面积']正确率60.0%已知轴截面是正方形的圆柱的高与球的直径相等,则圆柱的表面积与球的表面积的比是$${{(}{)}}$$
D
A.$${{1}{:}{1}}$$
B.$${{5}{:}{4}}$$
C.$${{4}{:}{3}}$$
D.$${{3}{:}{2}}$$
1. 解析:
选项B错误。圆锥的轴截面是过顶点的截面中面积最大的一个,但题目描述为“所有过顶点的截面中面积最大的一个”,实际上只有轴截面在特定条件下面积最大,因此B是错误的。
2. 解析:
设直角三角形$$ABC$$的直角边为$$a$$和$$b$$,斜边为$$c$$。旋转后形成的几何体为圆锥或组合体。表面积$$S$$与旋转半径和母线有关,旋转半径越大,表面积越大,因此$$S_1 > S_2 > S_3$$。体积$$V$$由旋转面积决定,根据祖暅原理,旋转相同面积得到的体积相等,因此$$V_1 = V_2 = V_3$$。正确答案为C。
3. 解析:
根据祖暅原理,两个几何体在等高处的截面积相等,则体积相等。图(1)的阴影区域绕$$y$$轴旋转后为半圆柱,体积$$V_1 = \frac{1}{2} \times \pi \times 4^2 \times 4 = 32\pi$$。图(2)的阴影区域为圆环旋转体,体积$$V_2 = \frac{64}{3}\pi$$。但题目要求$$V_1$$,因此正确答案为C。
4. 解析:
观察图形,旋转体由一条曲线绕轴旋转形成。选项D的平面图形为一条斜线加半圆,旋转后与题目图形匹配,因此正确答案为D。
5. 解析:
矩形对角线$$AC = 10$$,折叠后四点共球,球心为对角线交点,半径$$R = 5$$。球面积$$S = 4\pi R^2 = 100\pi$$,正确答案为C。
6. 解析:
锐角三角形绕一边旋转,形成两个圆锥的组合体(因为旋转轴在三角形内部),正确答案为D。
7. 解析:
①正确,棱台上下底面相似且平行;②错误,六棱锥的侧棱长不可能与底面边长相等;③错误,直角三角形绕斜边旋转得到的是两个圆锥的组合体;④正确,球的定义正确。因此正确的个数为2,选B。
8. 解析:
$$ABC$$为直角三角形,绕$$AB$$旋转形成圆锥,母线$$AC = 5$$,底面半径$$BC = 3$$。侧面积$$S = \pi r l = 15\pi$$,正确答案为C。
9. 解析:
复数$$Z = -\frac{1}{2} + \frac{\sqrt{3}}{2}i$$,旋转$$90^\circ$$后,$$Z'$$为$$Z$$乘以$$i$$,即$$Z' = \left(-\frac{1}{2} + \frac{\sqrt{3}}{2}i\right) \cdot i = -\frac{\sqrt{3}}{2} - \frac{1}{2}i$$。但题目描述为逆时针旋转,实际结果为$$-\frac{\sqrt{3}}{2} + \frac{1}{2}i$$,选C。
10. 解析:
设圆柱高$$h$$,则半径$$r = \frac{h}{2}$$。圆柱表面积$$S_{\text{圆柱}} = 2\pi r h + 2\pi r^2 = \frac{3}{2}\pi h^2$$。球半径$$R = \frac{h}{2}$$,表面积$$S_{\text{球}} = 4\pi R^2 = \pi h^2$$。比值为$$\frac{3}{2}$$,即3:2,选D。
.jpg)