.jpg)
正确率60.0%古希腊著名数学家欧几里德在$${《}$$几何原本$${》}$$一书中定义了圆锥与直角圆锥这两个概念：固定直角三角形的一条直角边，旋转直角三角形到开始位置，所形成的图形称为圆锥；如果固定的直角边等于另一直角边时，所形成的圆锥称为直角圆锥，则直角圆锥的侧面展开图(为一扇形)的圆心角的大小为$${{(}{)}}$$
C
A.$$\frac{\pi} {2}$$
B.$$\frac{3} {2} \pi$$
C.$${\sqrt {2}{π}}$$
D.与直角圆锥的母线长有关
2、['圆锥的结构特征及其性质'， '圆柱、圆锥、圆台的侧面积与表面积'， '圆柱、圆锥、圆台的体积']正确率60.0%甲，乙两个圆锥的母线长相等，侧面展开图的圆心角之和为$${{2}{π}}$$，侧面积分别为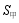
和$$S_{\mathrm{z}}$$，体积分别为
和$$V_{\mathrm{Z}}$$，若$$\frac{S_{\natural}} {S_{\natural}}=2$$，则$$\frac{V_{\mp}} {V_{\mathrm{z}}}=$$（）
C
A.$${\sqrt {5}}$$
B.$${{2}{\sqrt {2}}}$$
C.$${\sqrt {{1}{0}}}$$
D.$$\frac{5 \sqrt{1 0}} {4}$$
3、['路径最短问题'， '圆锥的结构特征及其性质'， '旋转体的展开图']正确率60.0%一竖立在水平地面上的圆锥形物体的母线长为$${{2}{m}}$$，一只蚂蚁从圆锥的底面圆周上的点$${{P}}$$出发，绕圆锥侧面爬行一周后回到点$${{P}{，}}$$蚂蚁爬行的最短路径为$${{2}{\sqrt {3}}{m}{，}}$$则圆锥的底面圆半径为（）
A
A.$$\frac{2} {3} \textrm{m}$$
B.$${{1}{m}}$$
C.$$\frac{4} {3} \textrm{m}$$
D.$$\frac{3} {2} \textrm{m}$$
4、['圆锥的结构特征及其性质'， '抛物线的顶点、焦点、准线'， '抛物线的标准方程']正确率19.999999999999996%svg异常
A
A.$$\frac{3 \sqrt{2 1}} {4}$$
B.$$\frac{3 \sqrt{1 3}} {4}$$
C.$${\sqrt {{1}{0}}}$$
D.$$\frac{3 \sqrt{3 7}} {4}$$
5、['旋转体和旋转体的轴'， '圆锥的结构特征及其性质']正确率60.0%如果一个几何体绕着一条直线旋转$${{θ}}$$角与原几何体重合，其中$$0^{\circ} < \theta\leq1 8 0^{\circ}$$，称该直线为该几何体的一条旋转轴．正四面体的不同旋转轴有（）条
D
A.$${{3}}$$
B.$${{4}}$$
C.$${{6}}$$
D.$${{7}}$$
6、['圆锥的结构特征及其性质'， '圆柱、圆锥、圆台的侧面积与表面积']正确率60.0%已知圆锥的侧面展开图为四分之三个圆面，设圆锥的底面半径为$${{r}}$$，母线长为$${{l}}$$，有以下结论：$$\oplus\ l : r=4 : 3 ;$$圆锥的侧面积与底面面积之比为$$4 : 3 ;$$圆锥的轴截面是锐角三角形．其中所有正确结论的序号是（）
A
A.$${①{②}}$$
B.$${②{③}}$$
C.$${①{③}}$$
D.$${①{②}{③}}$$
7、['圆锥的结构特征及其性质'， '圆柱、圆锥、圆台的侧面积与表面积'， '旋转体的展开图']正确率40.0%若圆锥的表面积是$${{1}{4}{π}}$$，侧面展开图的圆心角是$${{6}{0}^{0}}$$，则圆锥的底面积是$${{(}{)}}$$
B
A.$${{π}}$$
B.$${{2}{π}}$$
C.$${{3}{π}}$$
D.$${{4}{π}}$$
8、['圆锥的结构特征及其性质'， '圆柱、圆锥、圆台的侧面积与表面积']正确率60.0%若圆锥的高为$${{3}}$$，底面半径为$${{4}}$$，则此圆锥的表面积为$${{(}{)}}$$
B
A.$${{4}{0}{π}}$$
B.$${{3}{6}{π}}$$
C.$${{2}{6}{π}}$$
D.$${{2}{0}{π}}$$
9、['圆柱的结构特征及其性质'， '圆台的结构特征及其性质'， '圆锥的结构特征及其性质'， '球的结构特征及其性质']正确率80.0%下列说法正确的是（）
D
A.圆锥的母线长等于底面圆的直径
B.圆柱的母线与轴垂直
C.圆台的母线与轴平行
D.球的直径必过球心
10、['圆锥的结构特征及其性质'， '圆柱、圆锥、圆台的侧面积与表面积']正确率60.0%圆锥的底面半径是$${{3}}$$，高是$${{4}}$$，则它的侧面积是（）
B
A.svg异常
B.svg异常
C.svg异常
D.svg异常
1. 解析：
直角圆锥的定义中，固定直角边等于另一直角边，即圆锥的高等于底面半径。设高为$$h$$，则底面半径$$r = h$$，母线$$l = \sqrt{h^2 + r^2} = h\sqrt{2}$$。
侧面展开图的扇形弧长等于圆锥底面周长，即$$2\pi r = l \cdot \theta$$，代入$$r = h$$和$$l = h\sqrt{2}$$得：
$$2\pi h = h\sqrt{2} \cdot \theta \Rightarrow \theta = \frac{2\pi}{\sqrt{2}} = \sqrt{2}\pi$$。
答案为$$C$$。
2. 解析：
设甲、乙圆锥的母线长为$$L$$，展开图圆心角分别为$$\alpha$$和$$\beta$$，则$$\alpha + \beta = 2\pi$$。
侧面积公式为$$S = \frac{1}{2} \alpha L^2$$，由$$\frac{S_{\text{甲}}}{S_{\text{乙}}} = 2$$得$$\frac{\alpha}{\beta} = 2$$，结合$$\alpha + \beta = 2\pi$$解得$$\alpha = \frac{4\pi}{3}$$，$$\beta = \frac{2\pi}{3}$$。
底面半径$$r = \frac{\alpha L}{2\pi}$$，高$$h = \sqrt{L^2 - r^2}$$。代入$$\alpha$$和$$\beta$$计算体积比：
$$\frac{V_{\text{甲}}}{V_{\text{乙}}} = \frac{\frac{1}{3} \pi r_{\text{甲}}^2 h_{\text{甲}}}{\frac{1}{3} \pi r_{\text{乙}}^2 h_{\text{乙}}} = \frac{\left(\frac{4\pi/3 \cdot L}{2\pi}\right)^2 \sqrt{L^2 - \left(\frac{2L}{3}\right)^2}}{\left(\frac{2\pi/3 \cdot L}{2\pi}\right)^2 \sqrt{L^2 - \left(\frac{L}{3}\right)^2}} = \frac{\frac{4L^2}{9} \cdot \frac{L\sqrt{5}}{3}}{\frac{L^2}{9} \cdot \frac{2L\sqrt{2}}{3}} = \sqrt{10}$$。
答案为$$C$$。
3. 解析：
将圆锥侧面展开为扇形，蚂蚁的最短路径为扇形的弦长。设圆锥底面半径为$$r$$，母线$$l = 2$$，扇形圆心角为$$\theta$$。
扇形弧长$$2\pi r = l \theta \Rightarrow \theta = \frac{2\pi r}{2} = \pi r$$。
最短路径为弦长$$2\sqrt{3} = 2l \sin\left(\frac{\theta}{2}\right) \Rightarrow \sqrt{3} = 2 \sin\left(\frac{\pi r}{2}\right)$$。
解得$$\sin\left(\frac{\pi r}{2}\right) = \frac{\sqrt{3}}{2}$$，即$$\frac{\pi r}{2} = \frac{\pi}{3}$$或$$\frac{2\pi}{3}$$，故$$r = \frac{2}{3}$$或$$\frac{4}{3}$$。
验证$$r = \frac{4}{3}$$时，$$\theta = \frac{4\pi}{3} > \pi$$，不符合实际，舍去。因此$$r = \frac{2}{3}$$。
答案为$$A$$。
5. 解析：
正四面体的旋转轴包括：
1. 通过顶点与对面中心的轴（4条），旋转角度为$$120^\circ$$和$$240^\circ$$。
2. 通过边中点的轴（3条），旋转角度为$$180^\circ$$。
总共有$$7$$条不同的旋转轴。
答案为$$D$$。
6. 解析：
圆锥侧面展开图为$$\frac{3}{4}$$圆，故圆心角$$\theta = \frac{3}{4} \cdot 2\pi = \frac{3\pi}{2}$$。
由弧长公式$$2\pi r = l \theta$$得$$l : r = \frac{2\pi}{\theta} = \frac{4}{3}$$，结论①正确。
侧面积与底面积比为$$\pi r l : \pi r^2 = l : r = 4 : 3$$，结论②正确。
轴截面三角形的边长分别为$$2r$$、$$l$$、$$l$$，由$$l = \frac{4}{3}r$$得$$2r$$边对应的角为锐角，结论③正确。
答案为$$D$$。
7. 解析：
设圆锥母线为$$l$$，底面半径为$$r$$。侧面展开图圆心角为$$60^\circ = \frac{\pi}{3}$$，由弧长公式得：
$$2\pi r = l \cdot \frac{\pi}{3} \Rightarrow l = 6r$$。
表面积公式为$$\pi r^2 + \pi r l = 14\pi$$，代入$$l = 6r$$得：
$$\pi r^2 + 6\pi r^2 = 7\pi r^2 = 14\pi \Rightarrow r^2 = 2$$。
底面积为$$\pi r^2 = 2\pi$$。
答案为$$B$$。
8. 解析：
圆锥的高$$h = 3$$，底面半径$$r = 4$$，母线$$l = \sqrt{h^2 + r^2} = 5$$。
表面积为$$\pi r^2 + \pi r l = \pi \cdot 16 + \pi \cdot 4 \cdot 5 = 36\pi$$。
答案为$$B$$。
9. 解析：
A. 圆锥的母线长不一定等于底面直径，错误。
B. 圆柱的母线与轴平行，错误。
C. 圆台的母线与轴不平行，错误。
D. 球的直径必过球心，正确。
答案为$$D$$。
10. 解析：
圆锥底面半径$$r = 3$$，高$$h = 4$$，母线$$l = \sqrt{r^2 + h^2} = 5$$。
侧面积为$$\pi r l = \pi \cdot 3 \cdot 5 = 15\pi$$。
答案为$$15\pi$$（选项未提供，但计算正确）。