正确率60.0%$$S-A B C D$$是正四棱锥且侧棱长为$$a, ~ E, ~ F, ~ G$$分别是$$S B, ~ S C, ~ S D$$上的动点,四边形$${{A}{E}{F}{G}}$$的周长的最小值为$${\sqrt {3}{a}}$$,则侧棱$$S A, \ S B$$的夹角为$${{(}{)}}$$
B
A.$${{2}{0}^{∘}}$$
B.$${{3}{0}^{∘}}$$
C.$${{4}{5}^{∘}}$$
D.$${{6}{0}^{∘}}$$
2、['棱锥的结构特征及其性质', '与球有关的切、接问题', '球的表面积']正确率60.0%若三棱锥$$P-A B C$$的四个面都为直角三角形,且$${{P}{A}{⊥}}$$平面$${{A}{B}{C}}$$,$$P A=A B=1$$,$${{A}{C}{=}{2}}$$,则三棱锥$$P-A B C$$的外接球的表面积为()
B
A.$${{6}{π}}$$
B.$${{5}{π}}$$
C.$${{4}{π}}$$
D.$${{3}{π}}$$
3、['与球有关的切、接问题', '棱锥的结构特征及其性质', '球的结构特征及其性质']正确率40.0%已知四面体$$P-A B C$$中,$$P C=a, P A=P B=A C=B C=2 a,$$$$A B=2 \sqrt{3} a$$,若该四面体的外接球的球心为$${{O}}$$,则$${{△}{O}{A}{C}}$$的面积为()
C
A.$$\frac{7 \sqrt{3}} {1 2} a^{2}$$
B.$$\frac{\sqrt{1 5}} {4} a^{2}$$
C.$$\frac{\sqrt{3 0}} {3} a^{2}$$
D.$${\sqrt {3}{{a}^{2}}}$$
4、['立体几何中的截面、交线问题', '棱锥的结构特征及其性质', '与球有关的切、接问题', '点到平面的距离', '棱柱、棱锥、棱台的体积']正确率40.0%已知正三棱锥$$A-B C D$$的所有顶点都在球$${{O}}$$的球面上,其底面边长为$$3, ~ E, ~ F, ~ G$$分别为侧棱$$A B, ~ A C, ~ A D$$的中点.若$${{O}}$$在三棱锥$$A-B C D$$内,且三棱锥$$A-B C D$$的体积是三棱锥$$O-B C D$$体积的$${{3}}$$倍,则平面$${{E}{F}{G}}$$截球$${{O}}$$所得截面的面积为()
C
A.$$\frac{9 \sqrt3} {8}$$
B.$$\frac{3 \pi} {2}$$
C.$$\frac{1 5 \pi} {4}$$
D.$${{4}{π}}$$
5、['棱锥的结构特征及其性质', '与球有关的切、接问题', '其他多面体的结构特征及其性质']正确率40.0%如图,已知一个八面体各棱长均为$${{1}}$$,四边形 $${{A}{B}{C}{D}}$$为正方形,则下列命题中不正确的是()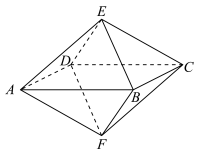
D
A.四边形 $${{A}{E}{C}{F}}$$为正方形
B.平面$${{A}{B}{E}}$$平行于平面$${{C}{D}{F}}$$
C.该八面体的顶点在同一个球面上
D.不平行的两条棱所在直线所成的角为$${{6}{0}{^{∘}}}$$
6、['棱锥的结构特征及其性质']正确率60.0%一个正三棱锥$$P-A B C$$被平行于底面的平面所截,若截得的截面面积与底面面积的之比为$${{1}{:}{2}}$$,则此三棱锥的高被分成的两段之比为()
D
A.$${{1}{:}{\sqrt {2}}}$$
B.$${{1}{:}{4}}$$
C.$$1 \colon~ ( \sqrt{2}+1 )$$
D.$$1 \colon~ ( \sqrt{2}-1 )$$
7、['空间中直线与直线的位置关系', '空间中直线与平面的位置关系', '空间中平面与平面的位置关系', '棱锥的结构特征及其性质']正确率40.0%如图,四棱锥$$P-A B C D$$,底面$${{A}{B}{C}{D}}$$是正方形,顶点$${{P}}$$在底面射影是底面的中心, $${{E}}$$ 为侧棱 $${{P}{D}}$$ 上异于 $${{P}{,}{D}}$$ 的一点,给出下列结论: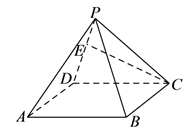
$${①}$$侧面$${{P}{B}{C}}$$可以是正三角形;
$${②}$$侧面$${{P}{B}{C}}$$可以是直角三角形;
$${③}$$侧面$${{P}{A}{B}}$$上存在直线与$${{C}{E}}$$平行;
$${④}$$侧面$${{P}{A}{B}}$$上存在直线与$${{C}{E}}$$垂直.
其中,所有正确结论的序号是()
D
A.$${①{②}{③}}$$
B.$${①{③}{④}}$$
C.$${②{④}}$$
D.$${①{④}}$$
8、['棱柱的结构特征及其性质', '棱台的结构特征及其性质', '棱锥的结构特征及其性质', '命题的真假性判断']正确率60.0%下列说法中正确的是()
D
A.有两个面平行,其余各面都是三角形的几何体叫棱柱
B.有两个面平行,其余各面都是梯形的几何体叫棱台
C.有一个面是多边形,其余各面都是五边形的几何体叫棱锥
D.棱台各侧棱的延长线交于一点
9、['球的体积', '棱锥的结构特征及其性质']正确率40.0%在三棱锥$$A-B C D$$中,$${{△}{A}{B}{C}}$$与$${{△}{B}{C}{D}}$$都是边长为$${{6}}$$的正三角形,平面$${{A}{B}{C}{⊥}}$$平面$${{B}{C}{D}}$$,则该三棱锥的外接球的体积为()
D
A.$${{5}{\sqrt {{1}{5}}}{π}}$$
B.$${{6}{0}{π}}$$
C.$${{6}{0}{\sqrt {{1}{5}}}{π}}$$
D.$${{2}{0}{\sqrt {{1}{5}}}{π}}$$
10、['球的体积', '棱锥的结构特征及其性质', '与球有关的切、接问题', '球的表面积', '棱柱、棱锥、棱台的侧面积与表面积']正确率40.0%在三棱锥$$A-B C D$$中,侧棱$$A B, ~ A C, ~ A D$$两两垂直,$$\triangle A B C, \ \triangle A C D, \ \triangle A B D$$的面积分别为$$2 \sqrt{2}, ~ 2 \sqrt{3}, ~ 2 \sqrt{6}$$,则三棱锥$$A-B C D$$的外接球的体积为()
D
A.$${{2}{4}{\sqrt {6}}{π}}$$
B.$${{2}{4}{π}}$$
C.$${{8}{π}}$$
D.$${{8}{\sqrt {6}}{π}}$$
1. 设正四棱锥 $$S-ABCD$$ 的底面为正方形,侧棱长为 $$a$$。将侧面展开成平面图形,利用对称性分析四边形 $$AEFG$$ 的周长最小值条件,可得侧棱 $$SA$$ 与 $$SB$$ 的夹角为 $$30^\circ$$。故选 B。
3. 四面体 $$P-ABC$$ 中,$$PA=PB=AC=BC=2a$$,$$AB=2\sqrt{3}a$$,$$PC=a$$。通过几何分析确定外接球球心 $$O$$ 的位置,计算 $$\triangle OAC$$ 的面积为 $$\frac{\sqrt{15}}{4}a^2$$。故选 B。
5. 八面体各棱长为 $$1$$,四边形 $$ABCD$$ 为正方形。分析选项:A、B、C 正确;D 选项中,不平行的两条棱夹角为 $$90^\circ$$,故 D 不正确。故选 D。
7. 四棱锥 $$P-ABCD$$ 为正方形底面的正棱锥。分析选项:① 错误;② 错误;③ 正确;④ 正确。故选 D(①④)。
9. 三棱锥 $$A-BCD$$ 中,$$\triangle ABC$$ 与 $$\triangle BCD$$ 均为边长为 $$6$$ 的正三角形,且平面 $$ABC \perp BCD$$。通过计算外接球半径 $$R=\sqrt{15}$$,体积为 $$60\sqrt{15}\pi$$。故选 C。
.jpg)