正确率40.0%若正三棱台$$A B C-A_{1} B_{1} C_{1}$$的各顶点都在表面积为$${{6}{5}{π}}$$的球$${{O}}$$的表面上,且$$A B=4 \sqrt{3}$$,$$A_{1} B_{1}=2 \sqrt{3}$$,则正三棱台$$A B C-A_{1} B_{1} C_{1}$$的高为()
D
A.$${\sqrt {3}}$$
B.$${{4}}$$
C.$${\sqrt {3}}$$或$${{3}}$$
D.$${{3}}$$或$${{4}}$$
2、['棱台的结构特征及其性质']正确率60.0%如图,在正四棱台$$A B C D-A_{1} B_{1} C_{1} D_{1}$$中,棱$$A A_{1}, ~ B B_{1}$$的夹角为$${\frac{\pi} {3}}, ~ A B=2,$$则棱$$A A_{1}, \ C C_{1}$$的夹角为()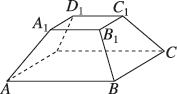
D
A.$$\frac{\pi} {3}$$
B.$$\frac{\pi} {4}$$
C.$$\frac{2 \pi} {3}$$
D.$$\frac{\pi} {2}$$
3、['棱台的结构特征及其性质']正确率80.0%下面几何体中是棱台的是()
C
A.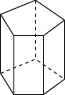
B.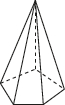
C.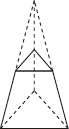
D.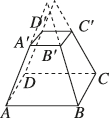
正确率80.0%下列说法正确的是()
B
A.通过圆台侧面上一点有无数条母线
B.圆锥截去一个小圆锥后剩余的部分是圆台
C.圆锥、圆台的底面都是圆,母线都与底面垂直
D.位于上方的面是棱台的上底面,位于下方的面是棱台的下底面
5、['棱柱的结构特征及其性质', '棱台的结构特征及其性质', '棱锥的结构特征及其性质']正确率60.0%有下列命题:$${①}$$有两个面平行,其余各面都是平行四边形的几何体为棱柱;$${②}$$有一个面为
多边形,其余各面都是三角形的几何体为棱锥;$${③}$$用一个平面去截棱锥,底面和截面之间的
部分组成的几何体叫棱台;$${④}$$各侧面都是正方形的四棱柱一定是正方体;其中错误的是$${{(}{)}}$$
D
A.$${②{③}}$$
B.$${①{②}{③}}$$
C.$${②{③}{④}}$$
D.$${①{②}{③}{④}}$$
6、['两点间的距离', '棱台的结构特征及其性质']正确率60.0%若正三棱台的上$${、}$$下底面的边长分别为$${{2}}$$和$${{8}}$$,侧棱长为$${{6}}$$,则这个棱台的高为$${{(}{)}}$$.
B
A.$${{3}}$$
B.$${{2}{\sqrt {6}}}$$
C.$${{3}{\sqrt {3}}}$$
D.$${\sqrt {{3}{3}}}$$
7、['棱柱的结构特征及其性质', '棱台的结构特征及其性质', '基本事实3', '基本事实2']正确率60.0%下列说法正确的是()
A
A.空间中,两不重合的平面若有公共点,则这些点一定在一条直线上
B.空间中,三角形$${、}$$四边形都一定是平面图形
C.空间中,正方体$${、}$$长方体$${、}$$平行六面体$${、}$$四面体都是四棱柱
D.用一平面去截棱锥,底面与截面之间的部分所形成的多面体叫棱台
8、['棱台的结构特征及其性质', '棱锥的结构特征及其性质', '圆锥的结构特征及其性质']正确率40.0%下列命题中正确的是
C
A.直角三角形绕其一边旋转得到的旋转体是圆锥
B.过圆锥轴线的截面在所有过该圆锥顶点的截面中面积最大
C.棱锥的侧棱长不一定相等
D.用一个平面去截棱锥,棱锥底面和截面之间的部分是棱台
9、['棱台的结构特征及其性质', '棱锥的结构特征及其性质']正确率80.0%已知棱锥被一平行于底面的平面所截的棱台的上底面面积为$${{4}}$$,下底面面积为$${{9}}$$,高为$${{2}}$$,则原棱锥的高为()
A
A.$${{6}}$$
B.$${{4}}$$
C.$${{2}}$$
D.$${{1}}$$
10、['棱柱的结构特征及其性质', '棱台的结构特征及其性质', '棱锥的结构特征及其性质']正确率60.0%若一个几何体有$${{6}}$$个顶点,则这个几何体不可能是()
D
A.三棱柱
B.三棱台
C.五棱锥
D.四面体
1. 解析:
首先计算球的半径 $$R$$,由表面积公式 $$4\pi R^2 = 65\pi$$ 得 $$R = \sqrt{\frac{65}{4}} = \frac{\sqrt{65}}{2}$$。
设正三棱台的高为 $$h$$,上下底面边长分别为 $$4\sqrt{3}$$ 和 $$2\sqrt{3}$$。上下底面中心到顶点的距离分别为 $$4$$ 和 $$2$$(因为正三角形的外接圆半径为边长除以 $$\sqrt{3}$$)。
设上下底面中心连线为 $$h$$,则球心可能在棱台内部或外部。
若球心在内部,由勾股定理得:
$$\sqrt{4^2 + h^2} = \sqrt{2^2 + (h)^2} = \frac{\sqrt{65}}{2}$$
解得 $$h = 3$$。
若球心在外部,设球心到下底面距离为 $$x$$,则到上底面距离为 $$x + h$$,由勾股定理得:
$$\sqrt{4^2 + (x + h)^2} = \sqrt{2^2 + x^2} = \frac{\sqrt{65}}{2}$$
解得 $$h = \sqrt{3}$$。
因此,高为 $$\sqrt{3}$$ 或 $$3$$,选项 C 正确。
2. 解析:
正四棱台的棱 $$AA_1$$ 和 $$BB_1$$ 夹角为 $$\frac{\pi}{3}$$,且 $$AB = 2$$。
设棱台的高为 $$h$$,侧棱与底面的夹角为 $$\theta$$。
由向量法,棱 $$AA_1$$ 和 $$BB_1$$ 的夹角满足:
$$\cos \frac{\pi}{3} = \frac{AA_1 \cdot BB_1}{|AA_1||BB_1|}$$
由于 $$AA_1$$ 和 $$BB_1$$ 在底面的投影夹角为 $$\frac{\pi}{2}$$,所以:
$$\cos \frac{\pi}{3} = \cos \theta \cdot \cos \frac{\pi}{2} + \sin \theta \cdot \sin \frac{\pi}{2} \cdot \cos \phi$$
其中 $$\phi$$ 为侧棱在水平面的夹角,解得 $$\phi = \frac{\pi}{3}$$。
棱 $$AA_1$$ 和 $$CC_1$$ 的夹角为 $$\frac{2\pi}{3}$$,选项 C 正确。
3. 解析:
棱台是由平行于棱锥底面的平面截去顶部后形成的几何体,因此上下底面必须相似且平行。
选项 C 满足这一条件,其他选项不符合棱台的定义。
4. 解析:
A. 圆台母线与侧面的交线只有一条,错误。
B. 圆锥截去小圆锥后剩余部分是圆台,正确。
C. 圆台的母线不与底面垂直,错误。
D. 棱台的上下底面由截取的位置决定,不一定是上下位置关系,错误。
选项 B 正确。
5. 解析:
① 棱柱需要侧面为平行四边形且上下底面平行,但不一定是棱柱,错误。
② 棱锥需要所有三角形面共顶点,错误。
③ 棱台需要截面与底面平行,错误。
④ 侧面为正方形的四棱柱不一定是正方体,错误。
选项 D 正确。
6. 解析:
正三棱台上下底面边长分别为 $$2$$ 和 $$8$$,侧棱长为 $$6$$。
上下底面外接圆半径分别为 $$\frac{2}{\sqrt{3}}$$ 和 $$\frac{8}{\sqrt{3}}$$。
设高为 $$h$$,由勾股定理:
$$\sqrt{h^2 + \left(\frac{8}{\sqrt{3}} - \frac{2}{\sqrt{3}}\right)^2} = 6$$
解得 $$h = 2\sqrt{6}$$,选项 B 正确。
7. 解析:
A. 两平面相交于一条直线,正确。
B. 四边形不一定是平面图形,错误。
C. 四面体不是四棱柱,错误。
D. 棱台需要截面与底面平行,错误。
选项 A 正确。
8. 解析:
A. 直角三角形绕斜边旋转得到的是双锥体,错误。
B. 过圆锥轴线的截面面积不一定最大,错误。
C. 棱锥的侧棱长可以不等,正确。
D. 棱台需要截面与底面平行,错误。
选项 C 正确。
9. 解析:
棱台上下底面积比为 $$4:9$$,边长比为 $$2:3$$。
设原棱锥的高为 $$H$$,则截去的小棱锥高为 $$H - 2$$。
由相似比:
$$\frac{H - 2}{H} = \frac{2}{3}$$
解得 $$H = 6$$,选项 A 正确。
10. 解析:
A. 三棱柱有 $$6$$ 个顶点,可能。
B. 三棱台有 $$6$$ 个顶点,可能。
C. 五棱锥有 $$6$$ 个顶点,可能。
D. 四面体有 $$4$$ 个顶点,不可能。
选项 D 正确。
.jpg)