正确率60.0%如图是一个简单多面体的表面展开图(沿图中虚线折叠即可还原),则这个多面体的顶点数为()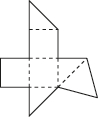
B
A.$${{6}}$$
B.$${{7}}$$
C.$${{8}}$$
D.$${{9}}$$
2、['多面体的展开图']正确率80.0%如图所示的$${{4}}$$个图中,不是正四面体的展开图的是()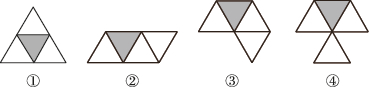
C
A.①③
B.②④
C.③④
D.①②
3、['路径最短问题', '多面体的展开图']正确率60.0%如图,已知正三棱柱$$A B C-A_{1} B_{1} C_{1}$$的底面边长为$${{1}{c}{m}{,}}$$高为$${{5}{c}{m}{,}}$$一质点自点$${{A}}$$出发,沿着三棱柱的侧面绕行两周到达点$${{A}_{1}}$$的最短路线的长为()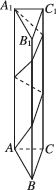
C
A.$${{1}{2}}$$
B.$${{1}{3}}$$
C.$${\sqrt {{6}{1}}}$$
D.$${{1}{5}}$$
4、['路径最短问题', '多面体的展开图']正确率40.0%古代数学名著$${《}$$数学九章$${》}$$中有云:$${{“}}$$有木长三丈,围之八尺,葛生其下,缠木两周,上与木齐,问葛长几何?$${{”}}$$意思为:圆木长$${{3}}$$丈,圆周为$${{8}}$$尺,葛藤从圆木的底部开始向上生长,绕圆木两周,刚好顶部与圆木平齐,问葛藤最少长多少尺(注:$${{1}}$$丈即$${{1}{0}}$$尺$${){(}}$$)
B
A.$${{3}{2}}$$尺
B.$${{3}{4}}$$尺
C.$${{3}{6}}$$尺
D.$${{3}{8}}$$尺
5、['空间中直线与直线的位置关系', '棱柱的结构特征及其性质', '多面体的展开图']正确率60.0%如图是正方体的侧面展开图,$${{L}_{1}{、}{{L}_{2}}}$$是两条侧面对角线,则在正方体中,$${{L}_{1}}$$与$${{L}_{2}{(}{)}}$$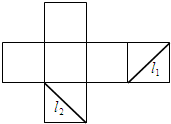
B
A.互相平行
B.相交
C.异面且互相垂直
D.异面且夹角为$${{6}{0}^{∘}}$$
6、['棱锥的结构特征及其性质', '多面体的展开图']正确率60.0%某人用如图所示的纸片沿折痕折后粘成一个四棱锥形的$${{“}}$$走马灯$${{“}}$$,正方形做灯底,且有一个三角形面上写上了$${{“}}$$年$${{”}}$$字,当灯旋转时,正好看到$${{“}}$$新年快乐$${{”}}$$的字样,则在$$\textcircled{1}, \ @,$$处可依次写上()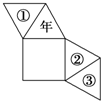
A
A.快$${、}$$新$${、}$$乐
B.乐$${、}$$新$${、}$$快
C.新$${、}$$乐$${、}$$快
D.乐$${、}$$快$${、}$$新
7、['棱柱的结构特征及其性质', '多面体的展开图']正确率60.0%如图是一个无盖的正方体盒子展开后的平面图,$$A, ~ B, ~ C$$是展开图上的三点,则在正方体盒子中,$${{∠}{A}{B}{C}}$$的值为()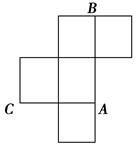
C
A.$${{3}{0}^{∘}}$$
B.$${{4}{5}^{∘}}$$
C.$${{6}{0}^{∘}}$$
D.$${{9}{0}^{∘}}$$
8、['路径最短问题', '多面体的展开图']正确率60.0%在三棱锥$$S \mathrm{-} \, A B C$$中,$$S A=S B=S C=1, \, \, \, \angle A S B=\angle A S C=\angle B S C=3 0^{\circ}$$,如图,一只蚂蚁从点$${{A}}$$出发沿三棱锥的表面爬行一周后又回到$${{A}}$$点,则蚂蚁爬过的最短路程为$${{(}{)}}$$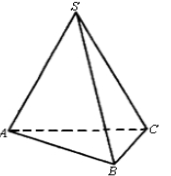
A
A.$${\sqrt {2}}$$
B.$${\sqrt {3}}$$
C.$${{2}{\sqrt {2}}}$$
D.$${{2}{\sqrt {3}}}$$
9、['异面直线所成的角', '多面体的展开图']正确率40.0%正方体的平面展开图如图,$$A B, C D, E F, G H$$四条对角线两两一对得到$${{6}}$$对对角线,在正方体中,这$${{6}}$$对对角线所在直线成$${{6}{0}^{∘}}$$角的有()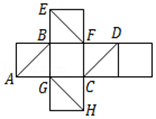
D
A.$${{1}}$$对
B.$${{2}}$$对
C.$${{3}}$$对
D.$${{4}}$$对
10、['空间中直线与直线的位置关系', '异面直线所成的角', '多面体的展开图']正确率60.0%一个正方体纸盒展开后如图所示,在原正方体纸盒中有如下结论:
①$$A B \perp E F$$;
②$$M N / / C D$$;
③$${{E}{F}}$$与$${{M}{N}}$$所成的角为$${{4}{5}^{∘}}$$;
④$${{A}{B}}$$与$${{M}{N}}$$所成的角为$${{6}{0}^{∘}}$$;
⑤$${{B}{C}}$$与$${{C}{D}}$$所成角的余弦值为$$\frac{\sqrt{6}} {3}$$.
以上四个命题中,所有正确命题的序号为()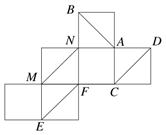
D
A.①②④
B.①③
C.②③⑤
D.①④⑤
1. 解析:
观察展开图,还原多面体后发现它是一个六棱锥,顶点数为7(6个底面顶点加1个锥顶)。
答案:$${{B}}$$
2. 解析:
正四面体的展开图需满足四个正三角形相连。分析选项可知③④不符合条件。
答案:$${{C}}$$
3. 解析:
将三棱柱侧面展开为矩形,绕行两周相当于展开两次。最短路径为对角线,计算得$${\sqrt{5^2 + (2 \times 3 \times 1)^2} = \sqrt{61}}$$。
答案:$${{C}}$$
4. 解析:
将圆木侧面展开为长方形,葛藤绕两周形成两条斜边。利用勾股定理计算斜边总长为$${\sqrt{(3 \times 10)^2 + (2 \times 8)^2} = 34}$$尺。
答案:$${{B}}$$
5. 解析:
还原正方体后,$$L_1$$与$$L_2$$为体对角线的投影,实际位置为异面直线且夹角$$60^\circ$$。
答案:$${{D}}$$
6. 解析:
根据旋转顺序和“年”字位置,推断其余三面依次为“乐”“新”“快”。
答案:$${{D}}$$
7. 解析:
还原正方体后,$$A, B, C$$三点构成等边三角形,故$${\angle ABC = 60^\circ}$$。
答案:$${{C}}$$
8. 解析:
展开三棱锥侧面,最短路径为平面内直线距离。通过余弦定理计算得$${\sqrt{1^2 + 1^2 - 2 \times 1 \times 1 \times \cos 90^\circ} = \sqrt{2}}$$。
答案:$${{A}}$$
9. 解析:
正方体中,四条对角线两两成$$60^\circ$$的共有3对(如$$AB$$与$$CD$$、$$EF$$与$$GH$$等)。
答案:$${{C}}$$
10. 解析:
还原正方体验证:①$$AB \perp EF$$正确;④$$AB$$与$$MN$$成$$60^\circ$$正确;⑤$$BC$$与$$CD$$余弦值为$${\frac{\sqrt{6}}{3}}$$正确。
答案:$${{D}}$$
.jpg)