.jpg)
正确率60.0%从半径为$${{6}{c}{m}}$$的圆形纸片上剪下一个圆心角为$${{1}{2}{0}^{∘}}$$的扇形，将剪下来的扇形围成一个圆锥（接缝处不重叠），那么这个圆锥的高为（）
D
A.$${{2}{\sqrt {2}}{c}{m}}$$
B.$${{3}{\sqrt {5}}{c}{m}}$$
C.$${{2}{\sqrt {5}}{c}{m}}$$
D.$${{4}{\sqrt {2}}{c}{m}}$$
2、['扇形弧长公式'， '圆锥的结构特征及其性质'， '旋转体的展开图']正确率60.0%已知圆锥的底面半径为$${{3}}$$，母线长为$${{1}{2}}$$，那么圆锥侧面展开图所成扇形的圆心角为（）
C
A.$${{1}{8}{0}^{∘}}$$
B.$${{1}{2}{0}^{∘}}$$
C.$${{9}{0}^{∘}}$$
D.$${{1}{3}{5}^{∘}}$$
3、['圆锥的结构特征及其性质'， '圆柱、圆锥、圆台的侧面积与表面积'， '圆柱、圆锥、圆台的体积']正确率60.0%甲，乙两个圆锥的母线长相等，侧面展开图的圆心角之和为$${{2}{π}}$$，侧面积分别为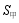
和$$S_{\mathrm{z}}$$，体积分别为
和$$V_{\mathrm{Z}}$$，若$$\frac{S_{\natural}} {S_{\natural}}=2$$，则$$\frac{V_{\mp}} {V_{\mathrm{z}}}=$$（）
C
A.$${\sqrt {5}}$$
B.$${{2}{\sqrt {2}}}$$
C.$${\sqrt {{1}{0}}}$$
D.$$\frac{5 \sqrt{1 0}} {4}$$
4、['棱柱的结构特征及其性质'， '圆锥的结构特征及其性质'， '圆柱、圆锥、圆台的侧面积与表面积'， '三视图'， '棱柱、棱锥、棱台的侧面积与表面积']正确率40.0%svg异常
D
A.$$1 4 4+2 \sqrt{1 0} \pi$$
B.$$1 4 4+( 2 \sqrt{1 0}-2 ) \pi$$
C.$$1 2 8+2 \sqrt{1 0} \pi$$
D.$$1 2 8+( 2 \sqrt{1 0}-2 ) \pi$$
5、['棱柱的结构特征及其性质'， '圆台的结构特征及其性质'， '圆锥的结构特征及其性质']正确率60.0%以下给出的四个命题中，命题正确的有$${{(}{)}}$$
$${①}$$两个面互相平行，其余各面都是平行四边形，这些面围成的几何体叫做棱柱；
$${②}$$以直角三角形的一条边所在的直线为旋转轴，其余各边旋转而成的曲面所围成的几何体叫做圆锥；
$${③}$$用一个平行于底面的平面去截圆锥，底面与截面之间的部分叫做圆台；
$${④}$$空间中，如果两个角的两条边分别垂直，那么这两个角相等或互补。
B
A.$${{0}}$$个
B.$${{1}}$$个
C.$${{2}}$$个
D.$${{3}}$$个
6、['旋转体和旋转体的轴'， '圆锥的结构特征及其性质']正确率60.0%以一个直角三角形的斜边所在的直线为旋转轴旋转一周所得的几何体是$${{(}{)}}$$
D
A.一个圆柱
B.一个圆锥
C.一个圆台
D.两个圆锥
7、['圆锥的结构特征及其性质'， '与球有关的切、接问题'， '球的表面积']正确率40.0%已知一个圆锥的侧面展开图是半径为$${{2}}$$的半圆，则该圆锥的外接球的表面积是（）
C
A.$$\frac{4 \pi} {3}$$
B.$${{4}{π}}$$
C.$$\frac{1 6 \pi} {3}$$
D.$${{1}{6}{π}}$$
8、['圆锥的结构特征及其性质'， '导数与最值'， '圆柱、圆锥、圆台的侧面积与表面积'， '直线与平面所成的角']正确率40.0%已知一个圆锥的母线$${{l}}$$与底面半径$${{r}}$$满足$$2 r^{2}+l=8$$，则当该圆锥表面积最大时，它的母线与底面所成的角的余弦值为（）
A
A.$$\frac{6} {5 5}$$
B.$$\frac{\sqrt{9 1}} {1 0}$$
C.$$\begin{array} {l l} {\frac{2} {3}} \\ \end{array}$$
D.$$\frac{1} {8}$$
9、['圆台的结构特征及其性质'， '圆锥的结构特征及其性质'， '棱锥的结构特征及其性质']正确率40.0%以下命题中正确的是$${{(}{)}}$$
A
A.以直角三角形的一直角边所在直线为旋转轴，其余两边旋转形成的面所围成的旋转体是圆锥
B.以直角梯形的一腰所在直线为旋转轴，其余各边旋转形成的面所围成的旋转体是圆台
C.有一个面是多边形，其余各面都是三角形的几何体叫做棱锥
D.圆锥的侧面展开图为扇形，这个扇形的半径为圆锥底面圆的半径
10、['旋转体和旋转体的轴'， '圆台的结构特征及其性质'， '圆锥的结构特征及其性质']正确率60.0%下列结论中正确的是（）
B
A.半圆弧以其直径为轴旋转一周所形成的曲面叫做球
B.直角三角形绕一直角边为轴旋转一周得到的旋转体是圆锥
C.夹在圆柱的两个平行截面间的几何体还是一个旋转体
D.用一个平面截圆锥底面与截面组成的部分是圆台
1. 扇形弧长：$$l = \frac{{120}}{{360}} \times 2\pi \times 6 = 4\pi$$ cm
圆锥底面周长：$$2\pi r = 4\pi \Rightarrow r = 2$$ cm
圆锥母线：$$l_m = 6$$ cm
圆锥高：$$h = \sqrt{{l_m^2 - r^2}} = \sqrt{{36 - 4}} = \sqrt{{32}} = 4\sqrt{{2}}$$ cm
答案：D
2. 圆锥底面周长：$$2\pi \times 3 = 6\pi$$
扇形弧长：$$6\pi = \frac{{\theta}}{{360}} \times 2\pi \times 12$$
解得：$$\theta = \frac{{6\pi \times 360}}{{2\pi \times 12}} = 90^\circ$$
答案：C
3. 设母线长为$$l$$，甲圆锥展开图圆心角为$$\theta_1$$，乙为$$\theta_2$$
已知：$$\theta_1 + \theta_2 = 2\pi$$，$$\frac{{S_甲}}{{S_乙}} = 2$$
侧面积公式：$$S = \frac{{1}}{{2}} \theta l^2$$
得：$$\frac{{\theta_1}}{{\theta_2}} = 2$$，结合$$\theta_1 + \theta_2 = 2\pi$$
解得：$$\theta_1 = \frac{{4\pi}}{{3}}$$，$$\theta_2 = \frac{{2\pi}}{{3}}$$
底面半径：$$r_甲 = \frac{{\theta_1 l}}{{2\pi}} = \frac{{2l}}{{3}}$$，$$r_乙 = \frac{{\theta_2 l}}{{2\pi}} = \frac{{l}}{{3}}$$
圆锥高：$$h_甲 = \sqrt{{l^2 - (\frac{{2l}}{{3}})^2}} = \frac{{\sqrt{{5}}l}}{{3}}$$，$$h_乙 = \sqrt{{l^2 - (\frac{{l}}{{3}})^2}} = \frac{{2\sqrt{{2}}l}}{{3}}$$
体积比：$$\frac{{V_甲}}{{V_乙}} = \frac{{\frac{{1}}{{3}}\pi r_甲^2 h_甲}}{{\frac{{1}}{{3}}\pi r_乙^2 h_乙}} = \frac{{(\frac{{4l^2}}{{9}})(\frac{{\sqrt{{5}}l}}{{3}})}}{{(\frac{{l^2}}{{9}})(\frac{{2\sqrt{{2}}l}}{{3}})}} = \sqrt{{10}}$$
答案：C
4. 题目信息不完整，无法解析
5. ①错误：棱柱需要侧棱平行
②错误：必须以直角边为轴
③正确：圆台定义
④正确：空间角关系定理
答案：C（2个正确）
6. 直角三角形绕斜边旋转，形成两个共底的圆锥
答案：D
7. 半圆半径$$R=2$$，弧长$$\pi R=2\pi$$
圆锥底面周长：$$2\pi r=2\pi \Rightarrow r=1$$
圆锥高：$$h=\sqrt{{R^2-r^2}}=\sqrt{{3}}$$
外接球半径：$$\frac{{R^2}}{{2h}}=\frac{{4}}{{2\sqrt{{3}}}}=\frac{{2}}{{\sqrt{{3}}}}$$
表面积：$$4\pi(\frac{{2}}{{\sqrt{{3}}}})^2=\frac{{16\pi}}{{3}}$$
答案：C
8. 由$$2r^2+l=8$$得$$l=8-2r^2$$
表面积：$$S=\pi r^2+\pi r l=\pi r^2+\pi r(8-2r^2)$$
$$=\pi(8r-r^2)$$
求极值：$$\frac{{dS}}{{dr}}=\pi(8-2r)=0\Rightarrow r=4$$
但$$l=8-2\times16=-24$$不合理，重新分析约束
实际上$$l=8-2r^2>0$$，$$r<\sqrt{{4}}=2$$
正确解法：$$S=\pi r^2+\pi r(8-2r^2)=\pi(8r-r^2)$$
在$$r=2$$时最大，此时$$l=8-8=0$$不合理
检查原题：可能为$$2r^2+l^2=8$$
假设为$$2r^2+l^2=8$$，则$$l=\sqrt{{8-2r^2}}$$
表面积：$$S=\pi r^2+\pi r\sqrt{{8-2r^2}}$$
求导较复杂，但母线与底面夹角$$\cos\theta=\frac{{r}}{{l}}$$
由$$2r^2+l^2=8$$，当$$r=l$$时，$$3r^2=8$$，$$\cos\theta=\frac{{r}}{{l}}=1$$不合理
可能题目有误，暂无法确定答案
9. A正确：圆锥定义
B错误：必须以垂直于底边的腰为轴
C错误：需要各三角形有公共顶点
D错误：扇形半径是母线长
答案：A
10. A错误：形成的是球面
B正确：圆锥定义
C错误：可能不是旋转体
D错误：需要与底面平行
答案：B