.jpg)
正确率80.0%
龙洗是我国著名的文物之一，因盆内有龙纹故称龙洗，为古代皇宫盥洗用具，其盆体可以近似看作一个圆台$${{.}}$$如图，现有一龙洗盆高$${{1}{5}{c}{m}}$$，盆口直径为$${{4}{0}{c}{m}}$$，盆底直径为$$2 0 c m.$$往盆内倒入水，当水深$${{6}{c}{m}}$$时，盆内水的体积近似为$${{(}{)}}$$
A.$$5 8 1 \pi c m^{3}$$
B.$$8 7 2 \pi c m^{3}$$
C.$$1 1 5 2 \pi c m^{3}$$
D.$$1 4 3 6 \pi c m^{3}$$
2、['旋转体及其相关概念'， '多面体']正确率80.0%关于圆台，下列说法正确的是$${{(}{)}}$$
A.圆台是以直角梯形的一腰所在直线为轴旋转一周所得的旋转体
B.圆台是以直角梯形的一底所在直线为轴旋转一周所得的旋转体
C.圆台是以直角三角形的斜边所在直线为轴旋转一周所得的旋转体
D.圆台是以等腰梯形上、下底中点的连线所在直线为轴旋转半周所得的旋转体
3、['旋转体及其相关概念'， '多面体']正确率80.0%圆台的一个底面周长为另一个底面周长的$${{2}}$$倍，母线长为$${{4}}$$，圆台侧面积为$${{6}{0}{π}}$$，则圆台较小底面半径为$${{(}{)}}$$
A.$${{5}}$$
B.$${{1}{0}}$$
C.$${{1}{5}}$$
D.$${{2}{0}}$$
4、['旋转体及其相关概念'， '棱柱、棱锥、棱台的表面积和体积']正确率80.0%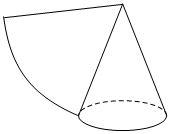
如图，圆锥的底面半径为$${{1}}$$，侧面展开图是一个圆心角为$${{6}{0}{°}}$$的扇形$${{.}}$$把该圆锥截成圆台，已知圆台的下底面与该圆锥的底面重合，圆台的上底面半径为$$\frac{1} {3}$$，则圆台的侧面积为$${{(}{)}}$$
A.$$\frac{8 \pi} {3}$$
B.$$\frac{\sqrt{3 5} \pi} {2}$$
C.$$\frac{1 6 \pi} {3}$$
D.$${{8}{π}}$$
5、['旋转体及其相关概念'， '棱柱、棱锥、棱台的表面积和体积']正确率40.0%已知圆锥的高为$${{1}}$$，体积为$${{π}}$$，则过圆锥顶点作圆锥截面的面积最大值为$${{(}{)}}$$
A.$${\sqrt {3}}$$
B.$${{2}}$$
C.$${{2}{\sqrt {3}}{π}}$$
D.$${{3}{π}}$$
6、['旋转体及其相关概念'， '棱柱、棱锥、棱台的表面积和体积']正确率80.0%若一个圆锥的底面积为$${{π}}$$，侧面展开图是一个半圆，则该圆锥的体积为$${{(}{)}}$$
A.$$\frac{\sqrt3} {3} \pi$$
B.$$\frac{\pi} {2}$$
C.$$\frac{\sqrt{2}} {2} \pi$$
D.$${{4}{π}}$$
7、['旋转体及其相关概念'， '棱柱、棱锥、棱台的表面积和体积']正确率80.0%已知某圆台的高为$${\sqrt {7}}$$，上底面半径为$${\sqrt {2}}$$，下底面半径为$${{2}{\sqrt {2}}}$$，则其侧面展开图的面积为$${{(}{)}}$$
A.$${{9}{π}}$$
B.$${{6}{\sqrt {2}}{π}}$$
C.$${{8}{\sqrt {2}}{π}}$$
D.$${{9}{\sqrt {2}}{π}}$$
8、['旋转体及其相关概念'， '棱柱、棱锥、棱台的表面积和体积']正确率80.0%已知圆锥的表面积为$${{3}{{m}^{2}}}$$，且它的侧面展开图是一个半圆，则这个圆锥底面的面积为$${{(}{)}}$$
A.$${{1}{{m}^{2}}}$$
B.$${\frac{3} {2}} m^{2}$$
C.$${{2}{{m}^{2}}}$$
D.$${\frac{5} {2}} m^{2}$$
9、['旋转体及其相关概念'， '棱柱、棱锥、棱台的表面积和体积']正确率80.0%已知圆锥的底面积为$${{1}}$$，表面积为$${{3}}$$，则它的侧面展开图的圆心角为$${{(}{)}}$$
A.$${{π}}$$
B.$$\frac{2 \pi} {3}$$
C.$$\frac{4 \pi} {3}$$
D.$$\frac{5 \pi} {3}$$
10、['旋转体及其相关概念'， '棱柱、棱锥、棱台的表面积和体积']正确率80.0%已知圆锥的高为$${\sqrt {3}}$$，底面半径为$${{3}}$$，则过此圆锥顶点的截面面积的最大值为$${{(}{)}}$$
A.$$\frac{3 \sqrt{3}} {2}$$
B.$${{3}{\sqrt {3}}}$$
C.$${{4}}$$
D.$${{6}}$$
1. 圆台的体积公式为 $$V = \frac{1}{3} \pi h (R^2 + Rr + r^2)$$，其中 $$h$$ 为高，$$R$$ 和 $$r$$ 分别为上下底半径。题目中水深 $$6 \text{cm}$$ 时，水形成的圆台的上底半径 $$r$$ 可通过比例关系计算：
圆台总高 $$15 \text{cm}$$，下底半径 $$10 \text{cm}$$，上底半径 $$20 \text{cm}$$。水深 $$6 \text{cm}$$ 时，水形成的圆台的上底半径 $$r$$ 满足比例关系：
$$\frac{r - 10}{20 - 10} = \frac{6}{15} \Rightarrow r = 14 \text{cm}$$
代入体积公式：
$$V = \frac{1}{3} \pi \times 6 \times (14^2 + 14 \times 10 + 10^2) = \frac{1}{3} \pi \times 6 \times (196 + 140 + 100) = 2 \pi \times 436 = 872 \pi \text{cm}^3$$
答案为 $$B$$。
2. 圆台的定义是以直角梯形的垂直于底边的腰所在直线为轴旋转一周所得的旋转体。因此选项 $$A$$ 正确。
答案为 $$A$$。
3. 设较小底面半径为 $$r$$，较大底面半径为 $$2r$$。圆台侧面积公式为 $$S = \pi (r_1 + r_2) l$$，代入已知条件：
$$60\pi = \pi (r + 2r) \times 4 \Rightarrow 60 = 12r \Rightarrow r = 5$$
答案为 $$A$$。
4. 圆锥的母线 $$l$$ 可通过扇形圆心角公式计算：
$$2\pi \times 1 = \frac{60^\circ}{360^\circ} \times 2\pi l \Rightarrow l = 6$$
圆台的母线 $$L$$ 通过相似三角形关系计算：
$$\frac{L}{6} = \frac{1 - \frac{1}{3}}{1} \Rightarrow L = 4$$
圆台侧面积公式为 $$S = \pi (r_1 + r_2) L$$，代入数据：
$$S = \pi \left(1 + \frac{1}{3}\right) \times 4 = \frac{16\pi}{3}$$
答案为 $$C$$。
5. 圆锥体积公式为 $$V = \frac{1}{3} \pi r^2 h$$，代入已知条件：
$$\pi = \frac{1}{3} \pi r^2 \times 1 \Rightarrow r = \sqrt{3}$$
过圆锥顶点的截面面积最大时为等腰直角三角形，面积为：
$$S = \frac{1}{2} \times 2r \times h = r \times h = \sqrt{3} \times 1 = \sqrt{3}$$
答案为 $$A$$。
6. 圆锥底面积为 $$\pi r^2 = \pi \Rightarrow r = 1$$。侧面展开图是半圆，说明母线 $$l = 2r = 2$$。圆锥的高 $$h$$ 为：
$$h = \sqrt{l^2 - r^2} = \sqrt{4 - 1} = \sqrt{3}$$
体积为：
$$V = \frac{1}{3} \pi r^2 h = \frac{\sqrt{3}}{3} \pi$$
答案为 $$A$$。
7. 圆台的母线 $$l$$ 为：
$$l = \sqrt{h^2 + (R - r)^2} = \sqrt{7 + (2\sqrt{2} - \sqrt{2})^2} = \sqrt{7 + 2} = 3$$
侧面积为：
$$S = \pi (r + R) l = \pi (\sqrt{2} + 2\sqrt{2}) \times 3 = 9\sqrt{2}\pi$$
答案为 $$D$$。
8. 设圆锥底面半径为 $$r$$，母线为 $$l$$。表面积公式为：
$$\pi r^2 + \pi r l = 3$$
侧面展开图是半圆，说明 $$2\pi r = \pi l \Rightarrow l = 2r$$。代入表面积公式：
$$\pi r^2 + \pi r \times 2r = 3 \Rightarrow 3\pi r^2 = 3 \Rightarrow r^2 = 1$$
底面积为 $$\pi r^2 = 1 \text{m}^2$$。
答案为 $$A$$。
9. 圆锥底面积为 $$1$$，表面积为 $$3$$，说明侧面积为 $$2$$。设底面半径为 $$r$$，母线为 $$l$$，则：
$$\pi r^2 = 1 \Rightarrow r = \frac{1}{\sqrt{\pi}}$$
侧面积公式为 $$\pi r l = 2 \Rightarrow l = \frac{2}{\sqrt{\pi}}$$
侧面展开图的圆心角 $$\theta$$ 满足：
$$2\pi r = \theta l \Rightarrow \theta = \frac{2\pi \times \frac{1}{\sqrt{\pi}}}{\frac{2}{\sqrt{\pi}}} = \pi$$
答案为 $$A$$。
10. 圆锥的高 $$h = \sqrt{3}$$，底面半径 $$r = 3$$。过圆锥顶点的截面面积最大时为等腰直角三角形，面积为：
$$S = \frac{1}{2} \times 2r \times h = r \times h = 3 \times \sqrt{3} = 3\sqrt{3}$$
答案为 $$B$$。