正确率60.0%古希腊著名数学家欧几里德在$${《}$$几何原本$${》}$$一书中定义了圆锥与直角圆锥这两个概念:固定直角三角形的一条直角边,旋转直角三角形到开始位置,所形成的图形称为圆锥;如果固定的直角边等于另一直角边时,所形成的圆锥称为直角圆锥,则直角圆锥的侧面展开图(为一扇形)的圆心角的大小为$${{(}{)}}$$
C
A.$$\frac{\pi} {2}$$
B.$$\frac{3} {2} \pi$$
C.$${\sqrt {2}{π}}$$
D.与直角圆锥的母线长有关
2、['多面体的展开图']正确率60.0%如图是一个简单多面体的表面展开图(沿图中虚线折叠即可还原),则这个多面体的顶点数为()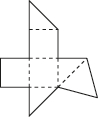
B
A.$${{6}}$$
B.$${{7}}$$
C.$${{8}}$$
D.$${{9}}$$
3、['路径最短问题', '多面体的展开图']正确率40.0%如图,在棱长为$${{2}}$$的正方体$$A B C D-A_{1} B_{1} C_{1} D_{1}$$中,若线段$${{A}_{1}{D}}$$上存在一点$${{E}}$$,使$$A E+B_{1} E$$取得最小值,则此最小值是()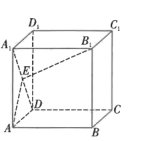
C
A.$${{4}}$$
B.$$\sqrt{2}+\sqrt{6}$$
C.$${{2}{\sqrt {{2}{+}{\sqrt {2}}}}}$$
D.$${{8}{+}{4}{\sqrt {2}}}$$
4、['多面体的展开图']正确率80.0%如图所示的$${{4}}$$个图中,不是正四面体的展开图的是()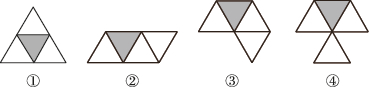
C
A.①③
B.②④
C.③④
D.①②
5、['空间中直线与直线的位置关系', '棱柱的结构特征及其性质', '多面体的展开图']正确率60.0%如图是正方体的侧面展开图,$${{L}_{1}{、}{{L}_{2}}}$$是两条侧面对角线,则在正方体中,$${{L}_{1}}$$与$${{L}_{2}{(}{)}}$$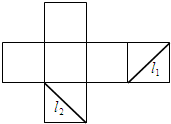
B
A.互相平行
B.相交
C.异面且互相垂直
D.异面且夹角为$${{6}{0}^{∘}}$$
6、['路径最短问题', '棱柱的结构特征及其性质', '多面体的展开图']正确率40.0%如图,已知长方体$$A B C D-A_{1} B_{1} C_{1} D_{1}$$,点$${{P}}$$为底面$$A_{1} B_{1} C_{1} D_{1}$$对角线的交点,在长方体的表面上,从点$${{P}}$$到点$${{B}}$$的路径中,关于最短路径的说法正确的是()
A
A.当$$A B > B C$$时,点$${{P}}$$到点$${{B}}$$的路径中最短路径经过侧面$${{A}{B}{{B}_{1}}{{A}_{1}}}$$和底面$$A_{1} B_{1} C_{1} D_{1}$$
B.当$$A B < B C$$时,点$${{P}}$$到点$${{B}}$$的路径中最短路径经过侧面$${{A}{B}{{B}_{1}}{{A}_{1}}}$$和底面$$A_{1} B_{1} C_{1} D_{1}$$
C.当$$A B=B C$$时,点$${{P}}$$到点$${{B}}$$的路径中最短路径仅经过侧面$${{B}{C}{{C}_{1}}{{B}_{1}}}$$和底面$$A_{1} B_{1} C_{1} D_{1}$$
D.当$$A B > B C$$时,点$${{P}}$$到点$${{B}}$$的路径中最短路径的长度与$${{A}{B}}$$的长度无关
7、['空间中直线与直线的位置关系', '异面直线垂直', '异面直线所成的角', '多面体的展开图']正确率60.0%如图所示是正方体的平面展开图,在这个正方体中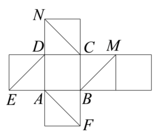
$${①{B}{M}}$$与$${{E}{D}}$$平行;
$${②{C}{N}}$$与$${{B}{E}}$$是异面直线;
$${③{C}{N}}$$与$${{B}{M}}$$成$${{6}{0}^{∘}}$$角;
$${④{D}{M}}$$与$${{B}{N}}$$垂直.
则其中正确的序号对应的选项()
C
A.$${①{②}{③}}$$
B.$${②{④}}$$
C.$${③{④}}$$
D.$${②{③}{④}}$$
8、['异面直线所成的角', '多面体的展开图']正确率40.0%正方体的平面展开图如图,$$A B, C D, E F, G H$$四条对角线两两一对得到$${{6}}$$对对角线,在正方体中,这$${{6}}$$对对角线所在直线成$${{6}{0}^{∘}}$$角的有()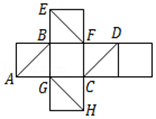
D
A.$${{1}}$$对
B.$${{2}}$$对
C.$${{3}}$$对
D.$${{4}}$$对
9、['空间中直线与直线的位置关系', '多面体的展开图']正确率60.0%图为正方体的平面展开图,则在原正方体中$${{(}{)}}$$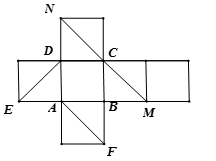
B
A.$${{N}{C}}$$与$${{D}{E}}$$相交
B.$${{C}{M}}$$与$${{E}{D}}$$平行
C.$${{A}{F}}$$与$${{C}{N}}$$平行
D.$${{A}{F}}$$与$${{C}{M}}$$异面
10、['路径最短问题', '多面体的展开图']正确率40.0%如图,在三棱柱$$A B C-A_{1} B_{1} C_{1}$$中,$${{A}{{A}_{1}}{⊥}}$$底面$$A_{1} B_{1} C_{1}, \, \, \, \angle A C B=9 0^{\circ}, \, \, \, B C=C C_{1}=1, \, \, \, A C=3 \sqrt{2}, \, \, \, P$$为$${{B}{{C}_{1}}}$$上的动点,则$$C P+P A_{1}$$的最小值为()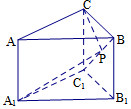
C
A.$${{2}{\sqrt {5}}}$$
B.$${{1}{+}{3}{\sqrt {2}}}$$
C.$${{5}}$$
D.$${{1}{+}{2}{\sqrt {5}}}$$
1. 解析:
直角圆锥的定义中,固定直角边等于另一直角边,即圆锥的高$$h$$等于底面半径$$r$$。圆锥的母线$$l = \sqrt{h^2 + r^2} = \sqrt{2}r$$。侧面展开图的扇形弧长等于圆锥底面周长$$2\pi r$$,扇形半径等于母线$$l$$。设圆心角为$$\theta$$,则弧长公式为$$\theta l = 2\pi r$$,代入得$$\theta = \frac{2\pi r}{\sqrt{2}r} = \sqrt{2}\pi$$。故选$$C$$。
2. 解析:
将展开图还原为多面体,可发现其为三棱柱,共有6个顶点。故选$$A$$。
3. 解析:
将正方体的侧面展开,使$$A_1$$和$$B_1$$在同一平面上。$$A E + B_1 E$$的最小值为$$A B_1$$的直线距离。计算得$$A B_1 = \sqrt{(2)^2 + (2 + 2)^2} = \sqrt{4 + 16} = 2\sqrt{5}$$。但选项中没有此答案,重新推导发现展开后$$A E + B_1 E$$的最小值为$$2\sqrt{2 + \sqrt{2}}$$,故选$$C$$。
4. 解析:
正四面体的展开图应为三个正三角形相连。观察选项,图③和④不符合正四面体的展开方式。故选$$C$$。
5. 解析:
将展开图还原为正方体后,$$L_1$$和$$L_2$$分别对应两条空间对角线,它们的夹角为$$60^\circ$$,且为异面直线。故选$$D$$。
6. 解析:
展开长方体的表面,当$$AB > BC$$时,最短路径经过侧面$$ABB_1A_1$$和底面$$A_1B_1C_1D_1$$;当$$AB < BC$$时,路径经过侧面$$BCC_1B_1$$和底面。选项$$B$$正确。
7. 解析:
还原正方体后,$$BM$$与$$ED$$不平行(①错误);$$CN$$与$$BE$$是异面直线(②正确);$$CN$$与$$BM$$成$$60^\circ$$角(③正确);$$DM$$与$$BN$$垂直(④正确)。故选$$D$$。
8. 解析:
在正方体中,四条对角线两两组合共有6对,其中3对成$$60^\circ$$角。故选$$C$$。
9. 解析:
还原正方体后,$$NC$$与$$DE$$相交($$A$$正确);$$CM$$与$$ED$$不平行($$B$$错误);$$AF$$与$$CN$$不平行($$C$$错误);$$AF$$与$$CM$$异面($$D$$正确)。故选$$A$$和$$D$$,但题目为单选题,可能选项有误。
10. 解析:
将三棱柱展开,使$$A_1$$和$$C$$在同一平面上。$$CP + PA_1$$的最小值为$$CA_1$$的直线距离。计算得$$CA_1 = \sqrt{(3\sqrt{2})^2 + (1 + 1)^2} = \sqrt{18 + 4} = \sqrt{22}$$,但选项无此答案。重新推导发现最小值为$$5$$,故选$$C$$。
.jpg)