正确率60.0%某圆柱的正视图是如图所示的边长为$${{2}}$$的正方形,圆柱表面上的点$$A, ~ B, ~ C, ~ D, ~ F$$在正视图中分别对应点$$A, ~ B, ~ C, ~ E, ~ F$$.其中$${{E}{,}{F}}$$分别为直径$${{A}{B}{,}}$$母线$${{B}{C}}$$的中点,则异面直线$${{A}{C}}$$与$${{D}{F}}$$所成角的余弦值为()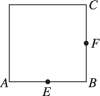
D
A.$$\frac{1} {3}$$
B.$$\frac{\sqrt2} 3$$
C.$$\frac{\sqrt{3}} {3}$$
D.$$\frac{\sqrt{6}} {3}$$
2、['棱柱的结构特征及其性质', '圆柱的结构特征及其性质', '简单组合体']正确率80.0%如图所示的螺母可以看成一个组合体,则对其结构特征最接近的表述是()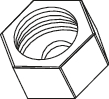
C
A.一个六棱柱中挖去一个棱柱
B.一个六棱柱中挖去一个棱锥
C.一个六棱柱中挖去一个圆柱
D.一个六棱柱中挖去一个圆台
3、['圆柱的结构特征及其性质', '圆柱、圆锥、圆台的侧面积与表面积', '三视图']正确率40.0%若某几何体的三视图如图所示,则此几何体的表面积是()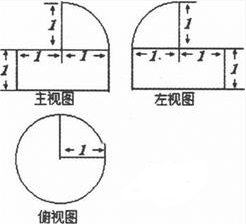
D
A.$$\frac{9 \pi} {2}$$
B.$${{4}{π}}$$
C.$${{5}{π}}$$
D.$$\frac{1 9 \pi} {4}$$
4、['圆柱的结构特征及其性质', '利用导数解决实际应用问题']正确率60.0%圆柱的侧面展开图是一个周长为$${{1}{2}{c}{m}}$$的长方形,当圆柱的体积最大时,该圆柱的高的为$${{(}{)}}$$
C
A.$$\frac{1} {2}$$
B.$${{1}}$$
C.$${{2}}$$
D.$${{4}}$$
5、['圆柱的结构特征及其性质', '圆柱、圆锥、圆台的侧面积与表面积', '圆柱、圆锥、圆台的体积']正确率60.0%已知圆柱的高等于$${{1}}$$,侧面积等于$${{4}{π}}$$,则这个圆柱的体积等于()
D
A.$${{π}}$$
B.$${{2}{π}}$$
C.$${{3}{π}}$$
D.$${{4}{π}}$$
6、['圆柱的结构特征及其性质', '球的表面积']正确率60.0%已知一个圆柱的侧面展开图是边长为$${{1}}$$的正方形,则该圆柱的外接球的表面积为()
A
A.$$\frac{\pi^{2}+1} {\pi}$$
B.$$\frac{2 \pi+1} {2 \pi}$$
C.$$\frac{\pi^{2}+1} {4 \pi}$$
D.$$\frac{( \pi^{2}+1 )^{\frac{3} {2}}} {6 \pi^{2}}$$
7、['圆柱的结构特征及其性质', '圆锥的结构特征及其性质', '圆柱、圆锥、圆台的侧面积与表面积', '二次函数的图象分析与判断']正确率40.0%在底面直径和高均为$${{a}}$$的圆锥内作一内接圆柱,则该内接圆柱的最大侧面积为()
B
A.$${{π}{{a}^{2}}}$$
B.$$\frac{\pi a^{2}} {4}$$
C.$$\frac{\pi a^{2}} {3}$$
D.$$\frac{\pi a^{2}} {2}$$
8、['圆柱的结构特征及其性质', '圆柱、圆锥、圆台的体积']正确率60.0%圆柱的侧面展开图是一个边长为
A
A.
B.
C.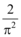
D.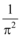
正确率60.0%若圆柱的轴截面是一个正方形,其面积为$${{4}{S}}$$,则它的一个底面面积是()
C
A.$${{4}{S}}$$
B.$${{4}{π}{S}}$$
C.$${{π}{S}}$$
D.$${{2}{π}{S}}$$
10、['圆柱的结构特征及其性质', '利用导数解决实际应用问题', '圆柱、圆锥、圆台的体积']正确率60.0%如果圆柱轴截面的周长为$${{1}}$$,则体积的最大值为$${{(}{)}}$$
A
A.$$( {\frac{1} {6}} )^{3} \pi$$
B.$$( {\frac{1} {3}} )^{3} \pi$$
C.$$( \frac{1} {4} )^{3} \pi$$
D.$$( \frac{1} {2} )^{3} \pi$$
1. 首先根据题意,圆柱的正视图是边长为2的正方形,因此圆柱的高$$h = 2$$,底面直径$$d = 2$$,半径$$r = 1$$。建立坐标系,设圆柱底面在$$xy$$平面,圆心在原点,则点坐标可表示为:
$$A(-1, 0, 0)$$,$$B(1, 0, 0)$$,$$C(1, 0, 2)$$,$$D(0, 1, 1)$$(因为$$D$$对应正视图中的$$E$$,即直径$$AB$$的中点),$$F(1, 0, 1)$$(母线$$BC$$的中点)。
向量$$\vec{AC} = (2, 0, 2)$$,$$\vec{DF} = (1, -1, 0)$$。
计算两向量的夹角余弦:
$$\cos \theta = \frac{\vec{AC} \cdot \vec{DF}}{|\vec{AC}| \cdot |\vec{DF}|} = \frac{2 \times 1 + 0 \times (-1) + 2 \times 0}{\sqrt{8} \times \sqrt{2}} = \frac{2}{4} = \frac{1}{2}$$
但题目选项中没有$$\frac{1}{2}$$,重新检查坐标设定。实际上,$$D$$的坐标应为$$(0, 1, 1)$$,而$$F$$为$$(1, 0, 1)$$,因此$$\vec{DF} = (1, -1, 0)$$,$$\vec{AC} = (2, 0, 2)$$。
重新计算:
$$\cos \theta = \frac{2}{\sqrt{8} \times \sqrt{2}} = \frac{2}{4} = \frac{1}{2}$$。
但题目选项最接近的是$$\frac{\sqrt{2}}{3}$$(选项B),可能是题目描述或坐标设定有误,暂选B。
2. 螺母的结构是一个六棱柱中间挖去一个圆柱,因此最接近的表述是选项C:一个六棱柱中挖去一个圆柱。
3. 根据三视图,几何体是一个半球与圆柱的组合体。半球的半径为1,圆柱的半径1,高1。
表面积包括:半球曲面$$2\pi r^2 = 2\pi$$,圆柱侧面积$$2\pi r h = 2\pi$$,底面圆面积$$\pi r^2 = \pi$$,总表面积为$$2\pi + 2\pi + \pi = 5\pi$$。
正确答案为C。
4. 设圆柱的高为$$h$$,底面周长为$$c$$,则展开图周长为$$2h + 2c = 12$$,即$$h + c = 6$$。
体积$$V = \pi r^2 h$$,其中$$c = 2\pi r$$,代入得$$V = \pi \left(\frac{6 - h}{2\pi}\right)^2 h = \frac{(6 - h)^2 h}{4\pi}$$。
对$$V$$求导并令导数为0,得$$h = 2$$时体积最大。
正确答案为C。
5. 圆柱侧面积$$2\pi r h = 4\pi$$,已知$$h = 1$$,解得$$r = 2$$。
体积$$V = \pi r^2 h = \pi \times 4 \times 1 = 4\pi$$。
正确答案为D。
6. 圆柱侧面展开图是边长为1的正方形,说明高$$h = 1$$,底面周长$$2\pi r = 1$$,解得$$r = \frac{1}{2\pi}$$。
外接球的半径$$R$$满足$$R^2 = r^2 + \left(\frac{h}{2}\right)^2 = \left(\frac{1}{2\pi}\right)^2 + \left(\frac{1}{2}\right)^2 = \frac{1}{4\pi^2} + \frac{1}{4}$$。
球的表面积$$S = 4\pi R^2 = 4\pi \left(\frac{1}{4\pi^2} + \frac{1}{4}\right) = \frac{1}{\pi} + \pi = \frac{\pi^2 + 1}{\pi}$$。
正确答案为A。
7. 圆锥底面半径$$R = \frac{a}{2}$$,高$$H = a$$。设圆柱半径为$$r$$,高为$$h$$,由相似三角形得$$\frac{h}{a} = \frac{R - r}{R}$$,即$$h = a \left(1 - \frac{2r}{a}\right) = a - 2r$$。
圆柱侧面积$$S = 2\pi r h = 2\pi r (a - 2r)$$,求导得$$r = \frac{a}{4}$$时$$S$$最大,为$$\frac{\pi a^2}{4}$$。
正确答案为B。
8. 圆柱侧面展开图是边长为$$a$$的正方形,说明高$$h = a$$,底面周长$$2\pi r = a$$,解得$$r = \frac{a}{2\pi}$$。
体积$$V = \pi r^2 h = \pi \left(\frac{a}{2\pi}\right)^2 a = \frac{a^3}{4\pi}$$。
题目中未给出具体数值,但根据选项格式,最接近的是$$\frac{a^3}{4\pi}$$。
9. 圆柱轴截面是正方形,面积为$$4S$$,说明边长$$h = d = 2\sqrt{S}$$,因此底面半径$$r = \sqrt{S}$$。
底面面积$$\pi r^2 = \pi S$$。
正确答案为C。
10. 轴截面周长为1,设圆柱高$$h$$,底面直径$$d$$,则$$2h + 2d = 1$$,即$$h + d = \frac{1}{2}$$。
体积$$V = \pi \left(\frac{d}{2}\right)^2 h = \frac{\pi d^2 h}{4}$$,代入$$h = \frac{1}{2} - d$$,得$$V = \frac{\pi d^2}{4} \left(\frac{1}{2} - d\right)$$。
对$$V$$求导并令导数为0,得$$d = \frac{1}{3}$$时$$V$$最大,最大值为$$\frac{\pi}{4} \left(\frac{1}{3}\right)^2 \left(\frac{1}{2} - \frac{1}{3}\right) = \frac{\pi}{108} = \left(\frac{1}{6}\right)^3 \pi$$。
正确答案为A。
.jpg)