.jpg)
正确率19.999999999999996%已知正四面体$$A-B C D$$的棱长为$${{2}}$$，点$${{E}}$$是$${{A}{D}}$$的中点，则下面四个命题中正确的是
D
A.$$\exists~ F \in B C， ~ E F \bot A C$$
B.$$\exists\ F \in B C， \ E F / \! / \， A C$$
C.$$\forall~ F \in B C， ~ E F \geq\sqrt{3}$$
D.$$\forall~ F \in B C， ~ E F \perp A D$$
2、['空间中直线与直线的位置关系'， '空间中直线与平面的位置关系'， '空间中平面与平面的位置关系']正确率80.0%设$${{m}}$$、$${{n}}$$是两条不同的直线，$${{α}}$$、$${{β}}$$、$${{γ}}$$是三个不同的平面$${{.}}$$下列命题中正确的命题是$${{(}{)}}$$
A.若$${{α}{/}{/}{β}}$$，$${{m}{⊥}{α}}$$，$${{n}{⊥}{β}}$$，则$${{m}{/}{/}{n}}$$
B.若$${{α}{⊥}{γ}}$$，$${{β}{⊥}{γ}}$$，则$${{α}{/}{/}{β}}$$
C.若$${{m}{/}{/}{α}}$$，$${{α}{/}{/}{β}}$$，则$${{m}{/}{/}{β}}$$
D.若$${{m}{/}{/}{n}}$$，$${{n}{/}{/}{α}}$$，则$${{m}{/}{/}{α}}$$
3、['空间中直线与平面的位置关系'， '点与直线、点与平面的位置关系']正确率60.0%若$${{P}}$$是平面$${{α}}$$外一点，则下列命题正确的是（）
D
A.过$${{P}}$$只能作一条直线与平面$${{α}}$$相交
B.过$${{P}}$$可作无数条直线与平面$${{α}}$$垂直
C.过$${{P}}$$只能作一条直线与平面$${{α}}$$平行
D.过$${{P}}$$可作无数条直线与平面$${{α}}$$平行
4、['空间中直线与平面的位置关系'， '多面体'， '与圆有关的轨迹问题']正确率40.0%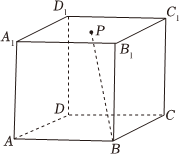
如图，正方体$$A B C D-A_{1} B_{1} C_{1} D_{1}$$的棱长为$${{1}}$$，点$${{P}}$$为正方形$$A_{1} B_{1} C_{1} D_{1}$$内的动点，满足直线$${{B}{P}}$$与下底面$${{A}{B}{C}{D}}$$所成角为$${{6}{0}{°}}$$的点$${{P}}$$的轨迹长度为$${{(}{)}}$$
A.$$\frac{\sqrt{3}} {3}$$
B.$$\frac{\sqrt{3}} {6} \pi$$
C.$${\sqrt {3}}$$
D.$$\frac{\sqrt3} {2} \pi$$
5、['空间中直线与平面的位置关系'， '直线与平面平行的性质定理'， '平面与平面平行的判定定理']正确率60.0%设$${{α}{，}{β}}$$是两个平面，$${{l}{，}{m}}$$是两条直线，下列各条件，可以判断$${{α}{/}{/}{β}}$$的有（）
$$\oplus\ l \subset\alpha， \ m \subset\alpha$$，且$$l / / \beta， ~ m / / \beta， ~ {\oplus} ~ l \subset\alpha， ~ m \subset\beta$$，且$$l / / \beta， ~ m / / \alpha， ~ \oplus l / / \alpha， ~ m / / \beta$$，且$$l / / m， \， \， \oplus l / / \alpha， \， \， l / / \beta， \， \， m / / \alpha， \， \， m / / \beta$$，且$${{l}{，}{m}}$$互为异面直线．
A
A.$${{1}}$$个
B.$${{2}}$$个
C.$${{3}}$$个
D.$${{4}}$$个
6、['全称量词命题的否定'， '空间中直线与平面的位置关系'， '充分、必要条件的判定']正确率60.0%下列说法正确的个数为$${{(}{)}}$$
$$\varpi\backslash\backslash;$$对于不重合的两条直线，$${{“}}$$两条直线的斜率相等$${{”}}$$是$${{“}}$$两条直线平行$${{”}}$$的必要不充分条件；
$$\textcircled{2} \backslash\backslash;$$命题$$\mathrm{` ` \wedge~} \mathrm{~ ` ` \wedge~} \mathrm{~ s i n} \， x \ll1^{\prime\prime}$$的否定是$$\mathrm{` `} \backslash\mathrm{e x i s t s} \; x_{0} \backslash\mathrm{i n} \; R， \; \; \operatorname{s i n} x_{0} > 1 "$$；
$$\textcircled{3} \backslash\backslash;^{\iota\varsigma} p$$且$${{q}}$$为真$${{”}}$$是$${{“}{p}}$$或$${{q}}$$为真$${{”}}$$的充分不必要条件；
已知直线$${{a}{，}{b}}$$和平面$${{α}{，}}$$若$$a \backslash{\bf p e r p} \， \alpha， \， \， b / / \alpha$$，则$$a \backslash\mathbf{p e r p} \， b$$．
C
A.$${{1}}$$
B.$${{2}}$$
C.$${{3}}$$
D.$${{4}}$$
7、['空间中直线与平面的位置关系'， '直线与平面垂直的性质定理']正确率60.0%如图，在四棱锥$$P-A B C D$$中，$${{P}{A}{⊥}}$$平面$$A B C D， ~ A D / \! / B C，$$ ，$$A D=A P=2， \， A B=B C=1$$ ，点$${{E}}$$ 是棱$${{P}{D}}$$ 的中点，$${{P}{C}}$$ 与平面$${{A}{B}{E}}$$ 交于点$${{F}}$$ ，设$$P F=\lambda P C$$ ，则$${{λ}{=}}$$ $${{(}{)}}$$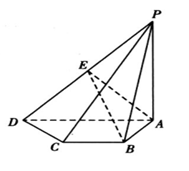 
C
A.$$\frac{5} {1 2}$$
B.$$\frac{1} {2}$$
C.$$\begin{array} {l l} {\frac{2} {3}} \\ \end{array}$$
D.$$\frac{3} {4}$$
8、['基本事实4'， '空间中直线与直线的位置关系'， '空间中直线与平面的位置关系'， '空间中平面与平面的位置关系'， '命题的真假性判断'， '直线与平面平行的判定定理']正确率40.0%下列命题中正确的是$${{(}{)}}$$
D
A.若直线$${{l}}$$上有无数个点不在平面$${{α}}$$内，则$${{1}{/}{/}{α}}$$
B.如果两条平行直线中的一条与一个平面平行，那么另一条也与这个平面平行
C.若两条直线都与第三条直线垂直，则这两条直线互相平行
D.垂直于同一个平面的两条直线互相平行
9、['空间中直线与直线的位置关系'， '空间中直线与平面的位置关系']正确率60.0%已知两条不同直线$${{l}_{1}}$$和$${{l}_{2}}$$及平面$${{α}{，}}$$则直线$$l_{1} / / l_{2}$$的一个充分条件是（）
D
A.$$l_{1} / / \alpha$$且$${{l}_{2}{⊂}{α}}$$
B.$$l_{1} / / \alpha$$且$$l_{2} / / \alpha$$
C.$$l_{1} / / \alpha$$且$${{l}_{2}{{⊂}{̸}}{α}}$$
D.$${{l}_{1}{⊥}{α}}$$且$${{l}_{2}{⊥}{α}}$$
10、['空间中直线与直线的位置关系'， '空间中直线与平面的位置关系'， '命题的真假性判断']正确率40.0%已知直线$${{a}{、}{b}}$$，平面$$\alpha， ~ \beta， ~ \gamma$$，下列命题正确的是（）
A
A.若$$\alpha\perp\gamma， \， \， \beta\perp\gamma， \， \， \， \alpha\cap\beta=a$$，则$${{a}{⊥}{γ}}$$
B.若$$\alpha\cap\beta=a， \， \， \， \alpha\cap\gamma=b， \， \， \， \beta\cap\gamma=c$$，则$$a / \! / b / \! / c$$
C.若$$\alpha\cap\beta=a， \， \， b / \! / a$$，则$${{b}{/}{/}{α}}$$
D.若$$\alpha\perp\beta， \， \， \， \alpha\cap\beta=a， \， \， \， b / / \alpha$$，则$${{b}{/}{/}{a}}$$
1. 解析：
正四面体 $$A-BCD$$ 棱长为 $$2$$，点 $$E$$ 是 $$AD$$ 的中点。
选项分析：
- A. 存在点 $$F \in BC$$ 使得 $$EF \perp AC$$。正确，因为可以在 $$BC$$ 上找到一点 $$F$$ 使得 $$EF$$ 与 $$AC$$ 垂直。
- B. 存在点 $$F \in BC$$ 使得 $$EF \parallel AC$$。错误，因为 $$EF$$ 与 $$AC$$ 不在同一平面内，无法平行。
- C. 对所有 $$F \in BC$$，$$EF \geq \sqrt{3}$$。错误，例如当 $$F$$ 为 $$BC$$ 中点时，$$EF = \sqrt{2}$$。
- D. 对所有 $$F \in BC$$，$$EF \perp AD$$。错误，因为 $$EF$$ 不一定垂直于 $$AD$$。
正确答案：$$A$$。
2. 解析：
选项分析：
- A. 若 $$\alpha \parallel \beta$$，$$m \perp \alpha$$，$$n \perp \beta$$，则 $$m \parallel n$$。正确，因为垂直于平行平面的直线平行。
- B. 若 $$\alpha \perp \gamma$$，$$\beta \perp \gamma$$，则 $$\alpha \parallel \beta$$。错误，例如两平面可能相交。
- C. 若 $$m \parallel \alpha$$，$$\alpha \parallel \beta$$，则 $$m \parallel \beta$$。错误，$$m$$ 可能在 $$\beta$$ 内。
- D. 若 $$m \parallel n$$，$$n \parallel \alpha$$，则 $$m \parallel \alpha$$。错误，$$m$$ 可能在 $$\alpha$$ 内。
正确答案：$$A$$。
3. 解析：
点 $$P$$ 在平面 $$\alpha$$ 外，选项分析：
- A. 过 $$P$$ 只能作一条直线与 $$\alpha$$ 相交。错误，可以作无数条。
- B. 过 $$P$$ 可作无数条直线与 $$\alpha$$ 垂直。错误，只能作一条。
- C. 过 $$P$$ 只能作一条直线与 $$\alpha$$ 平行。正确。
- D. 过 $$P$$ 可作无数条直线与 $$\alpha$$ 平行。错误，只能作一条。
正确答案：$$C$$。
4. 解析：
正方体 $$ABCD-A_1B_1C_1D_1$$ 棱长为 $$1$$，点 $$P$$ 在正方形 $$A_1B_1C_1D_1$$ 内，满足直线 $$BP$$ 与底面 $$ABCD$$ 所成角为 $$60^\circ$$。
轨迹为以 $$B_1$$ 为圆心，半径为 $$\frac{\sqrt{3}}{3}$$ 的圆弧，长度为 $$\frac{\sqrt{3}}{6}\pi$$。
正确答案：$$B$$。
5. 解析：
判断平面 $$\alpha \parallel \beta$$ 的条件：
- 第一条：两条直线在 $$\alpha$$ 内且平行于 $$\beta$$，可以推出 $$\alpha \parallel \beta$$。
- 第二条：两条直线分别在 $$\alpha$$ 和 $$\beta$$ 内且互相平行，不能推出 $$\alpha \parallel \beta$$。
- 第三条：两条直线分别平行于 $$\alpha$$ 和 $$\beta$$ 且互相平行，不能推出 $$\alpha \parallel \beta$$。
- 第四条：两条异面直线分别平行于 $$\alpha$$ 和 $$\beta$$，可以推出 $$\alpha \parallel \beta$$。
正确答案：$$B$$（2个）。
6. 解析：
选项分析：
- ①. 斜率相等是两直线平行的必要条件，但不充分（可能重合）。正确。
- ②. 命题 $$\sin x \leq 1$$ 的否定是 $$\exists x_0 \in \mathbb{R}, \sin x_0 > 1$$。正确。
- ③. $$p$$ 且 $$q$$ 为真是 $$p$$ 或 $$q$$ 为真的充分不必要条件。正确。
- ④. 若 $$a \perp \alpha$$，$$b \parallel \alpha$$，则 $$a \perp b$$。正确。
正确答案：$$D$$（4个）。
7. 解析：
四棱锥 $$P-ABCD$$ 中，$$PA \perp$$ 平面 $$ABCD$$，$$AD \parallel BC$$，$$AD=AP=2$$，$$AB=BC=1$$，点 $$E$$ 是 $$PD$$ 的中点，$$PC$$ 与平面 $$ABE$$ 交于点 $$F$$，设 $$PF = \lambda PC$$。
通过坐标法或向量法计算，可得 $$\lambda = \frac{1}{2}$$。
正确答案：$$B$$。
8. 解析：
选项分析：
- A. 直线 $$l$$ 上有无数点不在 $$\alpha$$ 内，不能推出 $$l \parallel \alpha$$（可能相交）。错误。
- B. 一条平行于平面，另一条不一定平行（可能在平面内）。错误。
- C. 两条直线都与第三条直线垂直，不一定平行（可能异面）。错误。
- D. 垂直于同一平面的两条直线平行。正确。
正确答案：$$D$$。
9. 解析：
直线 $$l_1 \parallel l_2$$ 的充分条件：
- A. $$l_1 \parallel \alpha$$ 且 $$l_2 \subset \alpha$$，不能推出 $$l_1 \parallel l_2$$（可能异面）。
- B. $$l_1 \parallel \alpha$$ 且 $$l_2 \parallel \alpha$$，不能推出 $$l_1 \parallel l_2$$（可能相交或异面）。
- C. $$l_1 \parallel \alpha$$ 且 $$l_2 \not\subset \alpha$$，不能推出 $$l_1 \parallel l_2$$。
- D. $$l_1 \perp \alpha$$ 且 $$l_2 \perp \alpha$$，可以推出 $$l_1 \parallel l_2$$。
正确答案：$$D$$。
10. 解析：
选项分析：
- A. 若 $$\alpha \perp \gamma$$，$$\beta \perp \gamma$$，$$\alpha \cap \beta = a$$，则 $$a \perp \gamma$$。正确。
- B. 三个平面两两相交，交线不一定平行（可能共点）。错误。
- C. 若 $$\alpha \cap \beta = a$$，$$b \parallel a$$，不能推出 $$b \parallel \alpha$$（可能在 $$\alpha$$ 内）。错误。
- D. 若 $$\alpha \perp \beta$$，$$\alpha \cap \beta = a$$，$$b \parallel \alpha$$，不能推出 $$b \parallel a$$（可能 $$b \perp \beta$$）。错误。
正确答案：$$A$$。