.jpg)
正确率60.0%已知$$a， ~ b， ~ c$$是两两不同的三条直线，下面四个命题中，真命题是（）
D
A.若直线$${{a}{，}{b}}$$异面$${，{b}{，}{c}}$$异面，则$${{a}{，}{c}}$$异面
B.若直线$${{a}{，}{b}}$$相交$${，{b}{，}{c}}$$相交，则$${{a}{，}{c}}$$相交
C.若$$a \perp b， ~ b \perp c，$$则$${{a}{/}{/}{c}}$$
D.若$$a / / b，$$则$${{a}{，}{b}}$$与$${{c}}$$所成的角相等
2、['空间中直线与平面的位置关系'， '空间中平面与平面的位置关系'， '平行关系的综合应用'， '异面直线'， '平面与平面平行的性质定理']正确率60.0%下列结论错误的个数是（ ）
（$${{1}}$$）若一条直线和平面内一条直线平行，那么这条直线和这个平面平行；
（$${{2}}$$）若直线$${{a}{/}{/}}$$平面$${{α}}$$，$${{P}{∈}{α}}$$，则过点$${{P}}$$且平行于直线$${{a}}$$的直线有无数条；
（$${{3}}$$）如果一个平面内的两条直线平行于另一个平面，那么这两个平面平行；
（4）如果两个平面平行，那么分别在这两个平面内的两条直线平行或异面.
C
A.$${{0}}$$
B.$${{1}}$$
C.$${{3}}$$
D.$${{2}}$$
3、['排列与组合的综合应用'， '异面直线'， '基本事实2']正确率60.0%两条异面直线$${{m}{，}{n}}$$上分别有$${{3}}$$个点和$${{4}}$$个点，这$${{7}}$$个点可以确定不同的平面个数为（）
C
A.$${{1}{2}}$$
B.$${{3}{0}}$$
C.$${{7}}$$
D.$${{1}{0}}$$
4、['空间中直线与直线的位置关系'， '空间中直线与平面的位置关系'， '异面直线']正确率60.0%已知直线$${{a}}$$，$${{b}}$$与平面$${{α}}$$，若$${{a}}$$平行$${{α}}$$，$${{b}}$$在$${{α}}$$内，则下列结论正确的是（）
D
A.$${{a}{/}{/}{b}}$$
B.$${{a}}$$与$${{b}}$$是异面直线
C.$${{a}{⊥}{b}}$$
D.以上情况都有可能
5、['棱柱的结构特征及其性质'， '空间两直线的共面、异面问题'， '异面直线']正确率40.0%正方体上的点$$P， ~ Q， ~ R， ~ S$$是其所在棱的中点，则直线$${{P}{Q}}$$与直线$${{R}{S}}$$异面的图形是$${{(}{)}}$$
B
A.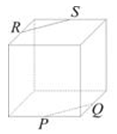
B.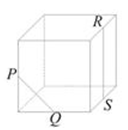
C.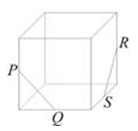
D.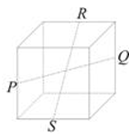
正确率40.0%已知$${{m}{，}{n}}$$是两条不同的直线，$${{α}{，}{β}}$$是两个不同的平面，则下列说法中正确的是
D
A.若$$m \subset\alpha， \， \， n \subset\alpha， \， \， m / / \beta， \， \， n / / \beta$$，则$${{α}{/}{/}{β}}$$
B.若$$m / / \alpha， \， \， n \subset\alpha$$，则$${{m}{/}{/}{n}}$$，
C.若$$m \subset\alpha， ~ m / / \beta， ~ n \subset\beta， ~ n / / \alpha$$，则$${{α}{/}{/}{β}}$$
D.若$${{m}{，}{n}}$$是异面直线，$$m \subset\alpha， ~ m / / \beta， ~ n \subset\beta， ~ n / / \alpha$$，则$${{α}{/}{/}{β}}$$
7、['空间中直线与直线的位置关系'， '异面直线'， '直线与平面垂直的判定定理'， '直线与平面平行的判定定理']正确率40.0%给出下列命题，其中错误命题的个数是$${{(}{)}}$$
$${①}$$若直线$${{a}}$$与平面$${{α}}$$平行，则直线$${{a}}$$与平面$${{α}}$$内的无数条直线平行；
$${②}$$若直线$${{a}}$$与平面$${{α}}$$垂直，则直线$${{a}}$$与平面$${{α}}$$的所有直线都垂直；
$${③}$$若异面直线$${{a}{，}{b}}$$垂直，则过直线$${{a}}$$的任何平面与$${{b}}$$都垂直；
$${④}$$若直线$${{a}}$$和直线$${{b}}$$共面，直线$${{b}}$$和直线$${{c}}$$共面，则直线$${{a}}$$和$${{c}}$$共面．
B
A.$${{1}}$$
B.$${{2}}$$
C.$${{3}}$$
D.$${{4}}$$
8、['异面直线'， '直线与平面垂直的性质定理']正确率60.0%菱形$${{A}{B}{C}{D}}$$在平面$${{α}}$$内，$${{P}{C}{⊥}{α}}$$，则$${{P}{A}}$$与对角线$${{B}{D}}$$的位置关系是（）
D
A.异面垂直
B.相交但不垂直
C.垂直相交
D.平行
9、['空间中直线与直线的位置关系'， '异面直线']正确率0.0%在三棱柱$$A B C-A_{1} B_{1} C_{1}$$中，$${{D}}$$为侧棱$${{C}{{C}_{1}}}$$的中点，从该三棱柱的九条棱中随机选取两条，则这两条棱所在直线至少有一条与直线$${{B}{D}}$$异面的概率是$${{(}{)}}$$
B
A.$$\begin{array} {l l} {\frac{2} {3}} \\ \end{array}$$
B.$$\frac{1 3} {1 8}$$
C.$$\begin{array} {l l} {7} \\ {\frac{7} {9}} \\ \end{array}$$
D.$$\frac{5} {6}$$
10、['异面直线']正确率80.0%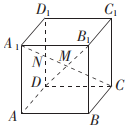
在正方体$$A B C D-A_{1} B_{1} C_{1} D_{1}$$中，点$${{M}}$$，$${{N}}$$分别是线段$${{D}{{B}_{1}}}$$和$${{A}_{1}{C}}$$上不重合的两个动点，则下列结论中正确的个数是$${{(}{)}}$$
①$$B C_{1} \perp M N$$；
②点$${{M}}$$在侧面$$D_{1} D C C_{1}$$上的投影在$${{D}_{1}{C}}$$上；
③$$B_{1} N / \! / C M$$；
④直线$${{B}{M}}$$与直线$${{A}_{1}{{D}_{1}}}$$为异面直线.
B
A.$${{0}}$$
B.$${{1}}$$
C.$${{2}}$$
D.$${{3}}$$
1. 解析：
2. 解析：
3. 解析：
4. 解析：
5. 解析：
6. 解析：
7. 解析：
8. 解析：
9. 解析：
10. 解析：