.jpg)
正确率80.0%下列说法正确的是$${{(}{)}}$$
A.过空间中的任意三点有且只有一个平面
B.三棱柱各面所在平面将空间分成$${{2}{1}}$$部分
C.空间中的三条直线$${{a}}$$，$${{b}}$$，$${{c}}$$，如果$${{a}}$$与$${{b}}$$异面，$${{b}}$$与$${{c}}$$异面，那么$${{a}}$$与$${{c}}$$异面
D.若直线$${{a}}$$在平面$${{α}}$$外，则平面$${{α}}$$内存在直线与$${{a}}$$平行
2、['空间中直线与平面的位置关系'， '平面']正确率80.0%下列命题中，正确的是$${{(}{)}}$$
A.一条直线和一个点确定一个平面
B.两个平面相交，可以只有一个公共点
C.三角形是平面图形
D.四边形是平面图形
3、['球的体积'， '平面']正确率40.0%已知球$${{O}}$$内切于正方体$$A B C D-A_{1} B_{1} C_{1} D_{1}$$，$${{P}}$$，$${{Q}}$$，$${{M}}$$，$${{N}}$$分别是$${{B}_{1}{{C}_{1}}}$$，$${{C}_{1}{{D}_{1}}}$$，$${{C}{D}}$$，$${{B}{C}}$$的中点，则该正方体及其内切球被平面$${{M}{N}{P}{Q}}$$所截得的截面面积之比为$${{(}{)}}$$
A.$${{4}{\sqrt {2}}}$$：$${{π}}$$
B.$${{2}{\sqrt {2}}}$$：$${{π}}$$
C.$${{3}{\sqrt {2}}}$$：$${{π}}$$
D.$${{4}}$$：$${{π}}$$
4、['多面体'， '平面']正确率80.0%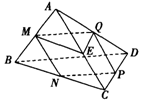
如图，在四面体$${{A}{B}{C}{D}}$$中，$${{M}}$$，$${{N}}$$，$${{P}}$$，$${{Q}}$$，$${{E}}$$分别是$${{A}{B}}$$，$${{B}{C}}$$，$${{C}{D}}$$，$${{A}{D}}$$，$${{A}{C}}$$的中点，则下列说法中不正确的是$${{(}{)}}$$
A.$${{M}}$$，$${{N}}$$，$${{P}}$$，$${{Q}}$$四点共面
B.$$\angle Q M E=\angle C B D$$
C.$${{△}{B}{C}{D}}$$∽$${{△}{M}{E}{Q}}$$
D.四边形$${{M}{N}{P}{Q}}$$为梯形
5、['多面体'， '平面']正确率80.0%下列各图中$${{P}}$$、$${{Q}}$$、$${{R}}$$、$${{S}}$$分别是各棱的中点，其中四个点不共面的图是$${{(}{)}}$$
A.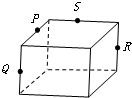
B.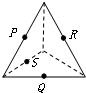
C.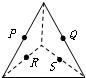
D.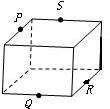
正确率80.0%从长方体的一个顶点出发的三条棱上各取一点$${{E}}$$、$${{F}}$$、$${{G}}$$，过此三点作长方体的截面，那么截去的几何体是$${{(}{)}}$$
A.三棱柱
B.三棱锥
C.四棱柱
D.四棱锥
7、['多面体'， '平面'， '棱柱、棱锥、棱台的表面积和体积']正确率0.0%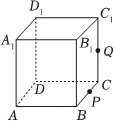
如图，正方体$$A B C D-A_{1} B_{1} C_{1} D_{1}$$的棱长为$${{6}}$$，$${{P}}$$为$${{B}{C}}$$的中点，$${{Q}}$$为$${{C}{{C}_{1}}}$$的中点，过点$${{A}_{1}}$$，$${{P}}$$，$${{Q}}$$的平面截正方体所得的截面的面积$${{S}{=}{(}{)}}$$
A.$$\frac{2 1 \sqrt{1 5}} {2}$$
B.$$\frac{2 1 \sqrt{1 7}} {2}$$
C.$$\frac{8 1 \sqrt{2}} {4}+9 \sqrt{6}$$
D.$$\frac{2 7 \sqrt{2}} {4}+9 \sqrt{6}$$
8、['多面体'， '平面']正确率80.0%在三棱锥$$P-A B C$$中，$$A B+2 P C=9$$，$${{E}}$$为线段$${{A}{P}}$$上更靠近$${{P}}$$的三等分点，过$${{E}}$$作平行于$${{A}{B}}$$，$${{P}{C}}$$的平面，则该平面截三棱锥$$P-A B C$$所得截面的周长为$${{(}{)}}$$
A.$${{5}}$$
B.$${{6}}$$
C.$${{8}}$$
D.$${{9}}$$
9、['多面体'， '平面']正确率80.0%
如图所示，该几何体是从一个水平放置的正方体中挖去一个内切球$${{(}}$$正方体各个面均与球面有且只有一个公共点$${{)}}$$以后而得到的，现用一竖直的平面去截这个几何体，则截面图形不可能是$${{(}{)}}$$
A.
B.
C.
D.
正确率80.0%下列说法正确的是$${{(}{)}}$$
A.圆柱上下底面各取一点，它们的连线即为圆柱的母线
B.过球上任意两点，有且仅有一个大圆
C.圆锥的轴截面是等腰三角形
D.用一个平面去截球，所得的圆即为大圆
1. 选项分析：
A. 错误。空间中三点共线时有无数个平面。
B. 正确。三棱柱的六个平面将空间分成21个部分。
C. 错误。a与c可能平行或相交。
D. 正确。直线a与平面α平行时存在，相交时也存在投影平行线。
正确答案：B、D
2. 选项分析：
A. 错误。点在直线上时不确定。
B. 错误。两平面相交于一条直线。
C. 正确。三角形一定是平面图形。
D. 错误。四边形可以是空间四边形。
正确答案：C
3. 解题步骤：
设正方体棱长为2，则球半径$$r=1$$。
截面MNPQ是正方形，边长$$\sqrt{2}$$，面积$$2$$。
球截面是圆，半径$$\frac{\sqrt{2}}{2}$$，面积$$\frac{π}{2}$$。
面积比$$4:π$$。
正确答案：D
4. 选项分析：
A. 正确。中点连线形成平行四边形。
B. 正确。$$\angle QME$$与$$\angle CBD$$对应边平行。
C. 正确。相似比为2:1。
D. 错误。MNPQ是平行四边形。
正确答案：D
5. 选项分析：
通过空间想象可知，只有D选项四点不共面。
正确答案：D
6. 几何分析：
截去部分是以顶点为锥顶的三棱锥。
正确答案：B
7. 解题步骤：
建立坐标系计算截面多边形顶点：
$$A_1(0,0,6)$$, $$P(6,3,0)$$, $$Q(6,6,3)$$
延长交$$D_1C_1$$于$$R(3,6,6)$$，形成五边形。
计算面积得$$\frac{21\sqrt{17}}{2}$$。
正确答案：B
8. 解题步骤：
设$$AB=x$$，$$PC=\frac{9-x}{2}$$。
根据平行截比定理，截面周长$$=x+\frac{9-x}{2}+\frac{2x}{3}+\frac{9-x}{3}=9$$。
正确答案：D
9. 选项分析：
竖直平面可能截得：
A. 带圆缺的矩形（可能）
B. 带圆弧的矩形（可能）
C. 纯矩形（可能）
D. 不可能出现图示直角缺口
正确答案：D
10. 选项分析：
A. 错误。连线必须平行轴线。
B. 错误。两点为直径端点时有无数大圆。
C. 正确。轴截面是等腰三角形。
D. 错误。只有过球心的截面才是大圆。
正确答案：C