正确率60.0%在长方体$$A B C D-A_{1} B_{1} C_{1} D_{1}$$中,直线$${{A}_{1}{C}}$$与平面$${{A}{{B}_{1}}{{D}_{1}}}$$的交点为$${{M}{,}{{A}_{1}}{{C}_{1}}}$$与$${{B}_{1}{{D}_{1}}}$$交于点$${{O}{,}}$$则下列结论正确的是()
B
A.$$A, ~ M, ~ O$$三点确定一个平面
B.$$A, ~ M, ~ O$$三点共线
C.$$D, ~ D_{1}, ~ O, ~ M$$四点共面
D.$$A, ~ B_{1}, ~ B, ~ M$$四点共面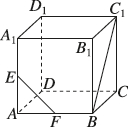
正确率80.0%下列说法正确的是()
C
A.桌面是平面
B.一个平面的面积是$${{2}{6}{{m}^{2}}}$$
C.空间图形是由点、线、面构成的
D.在空间图形中,原图中的线都要画成实线,后补画的线都画成虚线
3、['平面的相关概念及表示']正确率80.0%下列说法正确的是()
D
A.铺的很平的一张白纸是一个平面
B.平面是矩形或平行四边形
C.两个平面叠在一起比一个平面厚
D.平面的直观图一般画成平行四边形
4、['平面的相关概念及表示', '基本事实1']正确率80.0%经过同一条直线上的三个点的平面()
B
A.有且仅有$${{1}}$$个
B.有无数个
C.不存在
D.有且仅有$${{3}}$$个
5、['平面的相关概念及表示']正确率60.0%直线$$l_{1} / / l_{2}$$,在$${{l}_{1}}$$上取$${{3}}$$个点,在$${{l}_{2}}$$上取$${{2}}$$个点,由这$${{5}}$$个点能确定平面的个数为
A
A.$${{1}}$$
B.$${{4}}$$
C.$${{5}}$$
D.$${{9}}$$
6、['平面的相关概念及表示']正确率80.0%下列说法正确的是()
C
A.桌面是平面
B.一个平面的面积是$${{2}{6}{{m}^{2}}}$$
C.空间图形是由点、线、面构成的
D.用平行四边形表示平面,两个平面重叠在一起,比一个平面要厚
7、['立体几何中的四点共面、三点共线', '平面的相关概念及表示']正确率60.0%如图,四棱锥$$P-A B C D, \, \, \, A C \cap B D=O, \, \, \, M$$是$${{P}{C}}$$的中点,直线$${{A}{M}}$$交平面$${{P}{B}{D}}$$于点$${{N}}$$,则下列结论正确的是()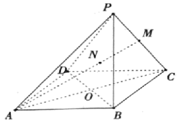
D
A.$$O, N, P, M$$四点不共面
B.$$O, N, M, D$$四点共面
C.$$O, N, M$$三点共线
D.$$P, N, O$$三点共线
8、['平面的相关概念及表示']正确率60.0%经过圆上任意三个不同的点可以作出
B
A.$${{0}}$$个
B.$${{1}}$$个
C.$${{2}}$$个
D.$${{1}}$$个或无数个
9、['平面的相关概念及表示', '分类加法计数原理']正确率60.0%已知两条异面直线$${{a}{,}{b}}$$上分别有$${{5}}$$个点和$${{8}}$$个点,则这$${{1}{3}}$$个点可以确定不同平面的个数为()
C
A.$${{4}{0}}$$
B.$${{1}{6}}$$
C.$${{1}{3}}$$
D.$${{1}{0}}$$
10、['平面的相关概念及表示']正确率80.0%点$${{A}}$$不在直线$${{a}}$$上,直线$${{a}}$$在平面$${{α}}$$内,点$${{B}}$$在平面$${{α}}$$内用符号语言表示为()
B
A.$$A \not\subset a, \, \, a \subset\alpha, \, \, \, B \in\alpha$$
B.$$A \notin a, \, \, a \subset\alpha, \, \, \, B \in\alpha$$
C.$$A \not\subset a, \, \, a \in\alpha, \, \, B \subset\alpha$$
D.$$A \notin a, \, \, a \in\alpha, \, \, \, B \in\alpha$$
1. 解析:
2. 解析:
3. 解析:
4. 解析:
5. 解析:
6. 解析:
7. 解析:
8. 解析:
9. 解析:
10. 解析:
.jpg)